Chapter 3, Problem 83P

(a)

To determine

The time taken for the stone to reach the base of the gorge.

Answer to Problem 83P

The time taken for the stone to reach the base of the gorge is $3.49\text{s}$ .

Explanation of Solution

Write the equation for the time taken for the stone to reach the base of the gorge.

    $t=\sqrt{\frac{2s}{g}}$        (I)

Here, $t$ is the time taken for the stone to reach the base of the gorge, $s$ is the height of the gorge and $g$ is the acceleration due to gravity.

Conclusion:

Substitute $60.0\text{m}$ for $s$ and $9.83{\text{m/s}}^2$ for $g$ in equation (I) to find $t$.

    $\begin{array}{c}t=\sqrt{\frac{2\left(60.0\text{m}\right)}{9.83{\text{m/s}}^2}}\\ =\sqrt{\frac{120.0\text{m}}{9.83{\text{m/s}}^2}}\\ =3.49\text{s}\end{array}$

Thus, the time taken for the stone to reach the base of the gorge is $3.49\text{s}$ .

(b)

To determine

The time taken for the stone to reach the ground if it is thrown straight down.

Answer to Problem 83P

The time taken for the stone to reach the ground if it is thrown straight down is $2.01\text{s}$.

Explanation of Solution

Write the equation for the vertical distance.

    $y=ut+\frac{1}{2}g{t}^2$        (II)

Here, $t$ is the time taken for the stone to reach the ground, $y$ is the vertical distance, $u$ is the initial velocity and $g$ is the acceleration due to gravity.

Rearrange equation (II),

    $\frac{1}{2}g{t}^2+ut-y=0$        (III)

Conclusion:

Substitute $20.0\text{m/s}$ for $u$, $60.0\text{m}$ for $y$ and $9.83{\text{m/s}}^2$ for $g$ in equation (I) to obtain a quadratic equation.

    $\frac{1}{2}\left(9.83{\text{m/s}}^2\right)t^2+\left(20.0\text{m/s}\right)t-60.0\text{m}=0$

The value of t can be found by solving the above quadratic equation.

  $t=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

Substitute $20.0\text{m/s}$ for $b$, $1/2$ for $a$, and $-60.0\text{m}$ for $c$ and solve.

    $\begin{array}{c}t=\frac{-\left(20.0\text{m/s}\right)\pm \sqrt{{\left(20.0\text{m/s}\right)}^2-4\left(\frac{1}{2}\right)\left(9.83{\text{m/s}}^2\right)\left(-60.0\text{m}\right)}}{2\left(\frac{1}{2}\right)\left(9.83{\text{m/s}}^2\right)}\\ =2.01\text{s or}-6.08\text{s}\end{array}$

As the time must be positive, the time taken for the stone to reach the ground if it is thrown straight down is $2.01\text{s}$.

(c)

To determine

The distance below the bridge the stone will hit the ground.

Answer to Problem 83P

The distance below the bridge the stone will hit the ground is $80.6\text{m}$.

Explanation of Solution

Figure 1 shows the components of velocities.

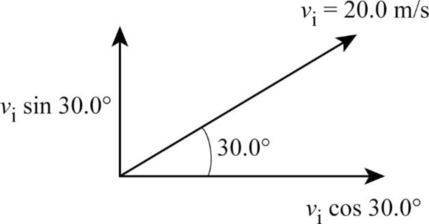
Figure 1

Write the equation for the vertical distance.

    $y=\left(u\sin \theta \right)t+\frac{1}{2}g{t}^2$        (III)

Here, $t$ is the time taken for the stone to reach the ground, $y$ is the vertical distance, $u$ is the initial velocity, $\theta$ is the projection angle and $g$ is the acceleration due to gravity.

Solve equation (III) ,

  $\frac{1}{2}g{t}^2+\left(u\sin \theta \right)t-y=0$        (IV)

Write the equation for the horizontal distance.

    $x=\left(u\cos \theta \right)t$        (V)

Conclusion:

Substitute $20.0\text{m/s}$ for $u$, $60.0\text{m}$ for $y$, $30.0°$ for $\theta$ and $9.83{\text{m/s}}^2$ for $g$ in equation (I) to obtain a quadratic equation.

    $\frac{1}{2}\left(9.83{\text{m/s}}^2\right)t^2-\left(20.0\text{m/s}\right)\sin 30.0°t-60.0\text{m}=0$

Find the value of $t$ by solving the quadratic equation.

  $t=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

Substitute $\left(20.0\text{m/s}\right)\sin 30.0$ for $b$, $\frac{1}{2}\left(9.83{\text{m/s}}^2\right)$ for $a$, and $-60.0\text{m}$ for $c$ and solve.

    $\begin{array}{c}t=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\\ =\frac{\left(20.0\text{m/s}\right)\sin 30.0°\pm \sqrt{{\left(20.0\text{m/s}\right)}^2{\sin }^{2}30.0°-4\left(\frac{1}{2}\right)\left(9.83{\text{m/s}}^2\right)\left(-60.0\text{m}\right)}}{2\left(\frac{1}{2}\right)\left(9.83{\text{m/s}}^2\right)}\\ =4.66\text{s or}-2.62\text{s}\end{array}$

As the time must be positive, the time taken is $4.66\text{s}$.

Substitute $20.0\text{m/s}$ for $u$, $30.0\text{s}$ for $\theta$ and $4.66\text{s}$ for $t$ in equation (V) to find $x$.

    $\begin{array}{c}x=\left(20.0\text{m/s}\right)\cos 30.0°\left(4.66\text{s}\right)\\ =80.6\text{m}\end{array}$

Therefore, the distance below the bridge the stone will hit the ground is $80.6\text{m}$.