Chapter 3, Problem 83CE

a.

To determine

Find the mean of the number of items.

Find the median of the number of items.

Answer to Problem 83CE

The mean of the number of items is 9.1.

The median of the number of items is 9.

Explanation of Solution

Calculation:

Step by step procedure to obtain mean, median using MINITAB software is given as,

• Choose Stat > Basic Statistics > Display Descriptive Statistics.
• In Variables enter the column Number of Items.
• Choose option statistics, and select Mean and Median.
• Click OK.

Output using MINITAB software is given below:

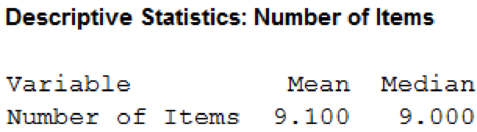
Hence, the mean of the number of items is 9.1, and the median of the number of items is 9.

b.

To determine

Find the range of the number of items.

Find the standard deviation of the number of items.

Answer to Problem 83CE

The range of the number of items is 14.

The standard deviation of the number of items is 3.566.

Explanation of Solution

Calculation:

Step by step procedure to obtain standard deviation and range using MINITAB software is given as,

• Choose Stat > Basic Statistics > Display Descriptive Statistics.
• In Variables enter the column Number of Items.
• Choose option statistics, and select standard deviation and range.
• Click OK.

Output using MINITAB software is given below:

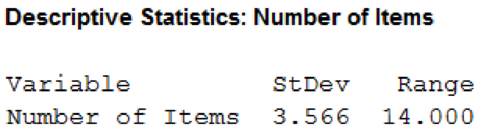
Hence, the range of the number of items is 14 and standard deviation of the number of items is 3.566.

c.

To determine

Find the frequency distribution for number of items.

Answer to Problem 83CE

The frequency distribution for number of items is,

Class	Frequency
3.5-6.5	10
6.5-9.5	6
9.5-12.5	9
12.5-15.5	4
15.5-18.5	1
Total	30

Explanation of Solution

Calculation:

Selection of number of classes:

The “2 to the k rule” suggests that the number of classes is the smallest value of k, where $2^k$ is greater than the number of observations.

Formula for class interval:

The formula for the class interval is given as follows:

$i\ge \frac{\left(\text{Maximum value}-\text{Minimum value}\right)}{k}$

Frequency distribution:

The frequency table is a collection of mutually exclusive and exhaustive classes that show the number of observations in each class.

Where, i is the class interval and k is the number of classes.

The data set consists of 30 observations. The value of k can be obtained as follows:

$\begin{array}{l}{2}^4=16<30\\ 2^5=32>30\end{array}$

Here, $k=5$ is the smallest value for which $2^k$ is greater than the number of observations. The number of classes for the given data set is 5.

The class interval is,

$\begin{array}{c}i\ge \frac{\left(\text{Maximum value}-\text{Minimum value}\right)}{k}\\ \ge \frac{18-4}{5}\\ \ge \frac{14}{5}\\ \ge 2.8\end{array}$

In practice, the class interval size is usually rounded up to some convenient number. Thus, the reasonable class interval is 3.

Since the minimum value is 4 and the class interval is 3, the first class would be 3.5-6.5.

The frequency distribution for duration in minutes can be constructed as follows:

Class	Frequency
3.5-6.5	10
6.5-9.5	6
9.5-12.5	9
12.5-15.5	4
15.5-18.5	1
Total	30

d.

To determine

Find the mean of the data.

Find the standard deviation of the data.

Compare these values with those computed in Part (a).

Explain why the values are different

Answer to Problem 83CE

The mean of the data is 9.

The standard deviation of the data is 3.553.

Explanation of Solution

Arithmetic mean of grouped data:

The mean of the data that is given in frequency distribution (grouped data) is calculated as,

$\overline{x}=\frac{{\displaystyle \sum fM}}{n}$

In the formula, $\overline{x}$ denotes the sample mean, M denotes the midpoint for each class, f denotes the frequency for each class, n denotes the total frequency.

Midpoint:

The midpoint is the average of the lower class limits of two consecutive classes. The formula is,

$\text{Midpoint}=\frac{\text{Lower}\text{limit}\text{of}\text{class}+\text{Lower}\text{limit}\text{of}\text{consecutive}\text{class}}{2}$

The frequency distribution table for mean is,

Class	Frequency f	M	$fM$
3.5-6.5	10	5	50
6.5-9.5	6	8	48
9.5-12.5	9	11	99
12.5-15.5	4	14	56
15.5-18.5	1	17	17
	$n=30$		${\displaystyle \sum fM}=270$

Substitute $n=30$ and ${\displaystyle \sum fM}=270$ in arithmetic mean formula.

$\begin{array}{c}\overline{x}=\frac{270}{30}\\ =9\end{array}$

Hence, the mean of the data is 9.

Standard deviation of grouped data:

The standard deviation of the data that is given in frequency distribution (grouped data) is calculated as,

$s=\sqrt{\frac{{\displaystyle \sum f{\left(M-\overline{x}\right)}^2}}{n-1}}$

In the formula, s denotes the sample standard deviation, $\overline{x}$ denotes the sample mean of grouped data, M denotes the midpoint for each class, f denotes the frequency for each class, n denotes the total frequency.

The value of mean is 9. The frequency distribution table for standard deviation is,

Class	Frequency f	M	$\left(M-\overline{x}\right)$	${\left(M-\overline{x}\right)}^2$	$f{\left(M-\overline{x}\right)}^2$
3.5-6.5	10	5	–4	16	160
6.5-9.5	6	8	–1	1	6
9.5-12.5	9	11	2	4	36
12.5-15.5	4	14	5	25	100
15.5-18.5	1	17	8	64	64
	$n=30$				${\displaystyle \sum f{\left(M-\overline{x}\right)}^2}=366$

Substitute $n=30$ and ${\displaystyle \sum f{\left(M-\overline{x}\right)}^2}=366$, in standard deviation formula.

$\begin{array}{c}s=\sqrt{\frac{366}{30-1}}\\ =\sqrt{\frac{366}{29}}\\ =\sqrt{12.6206896}\\ =3.553\end{array}$

Hence, the standard deviation of the data is 3.553.

The mean value is same for normal method and frequency distribution. But there is a slight change in the value of the standard deviation. This difference is due to using grouped data in frequency distribution. The frequency distribution only gives the estimate of the standard deviation because actual values of the data are not used.