Introductory and Intermediate Algebra for College Students, Books a la Carte Edition PLUS MyLab Math (5th Edition)
5th Edition
ISBN: 9780134584904
Author: Robert F. Blitzer
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 3, Problem 3MCP
To determine
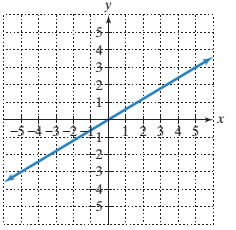
a)
The x−intercept of the line in the graph.
To determine
To calculate the x−intercept and y−intercept from the graph:
To find the x−intercept of a given line on a graph, the point where the line is intersecting the x−axis is the x−intercept and the point where the line is intersecting the y axis is the y−intercept.
To calculate the line’s slope:
Pick two points on the line and determine their coordinates.
Determine rise: the difference in y−coordinates of these two points.
Determine run: the difference in x−coordinates for these two points.
Divide the difference in y−coordinates by the difference in x−coordinates (rise/run or slope).
Given:
Line passing through the origin.
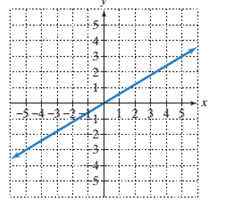
b)
To determine
The y−intercept of the line in the graph.
To determine
To calculate the x−intercept and y−intercept from the graph:
To find the x−intercept of a given line on a graph, the point where the line is intersecting the x−axis is the x−intercept and the point where the line is intersecting the y axis is the y−intercept.
To calculate the line’s slope:
Pick two points on the line and determine their coordinates.
Determine rise: the difference in y−coordinates of these two points.
Determine run: the difference in x−coordinates for these two points.
Divide the difference in y−coordinates by the difference in x−coordinates (rise/run or slope).
Given:
Line passing through the origin.
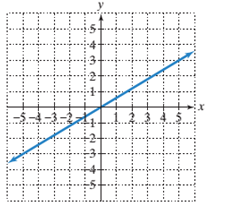
c)
To determine
The slope of line.
To determine
To calculate the x−intercept and y−intercept from the graph:
To find the x−intercept of a given line on a graph, the point where the line is intersecting the x−axis is the x−intercept and the point where the line is intersecting the y axis is the y−intercept.
To calculate the line’s slope:
Pick two points on the line and determine their coordinates.
Determine rise: the difference in y−coordinates of these two points.
Determine run: the difference in x−coordinates for these two points.
Divide the difference in y−coordinates by the difference in x−coordinates (rise/run or slope).
Given:
Line passing through the origin.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Safari
File Edit View History
Bookmarks
Window
Help
Ο Ω
OV
O mA
0 mW
ర
Fri Apr 4 1
222
tv
A
F9
F10
DII
4
F6
F7
F8
7
29
8
00
W
E
R
T
Y
U
S
D
பட
9
O
G
H
J
K
E
F11
+ 11
F12
O
P
}
[
So confused. Step by step instructions please
In simplest terms, Sketch the graph of the parabola. Then, determine its equation.
opens downward, vertex is (- 4, 7), passes through point (0, - 39)
Chapter 3 Solutions
Introductory and Intermediate Algebra for College Students, Books a la Carte Edition PLUS MyLab Math (5th Edition)
Ch. 3.1 - Fill in the blank so that the resulting statement...Ch. 3.1 - Fill in each blank so that the resulting statement...Ch. 3.1 - Prob. 3CAVCCh. 3.1 - Prob. 4CAVCCh. 3.1 - Prob. 5CAVCCh. 3.1 - Prob. 6CAVCCh. 3.1 - Prob. 7CAVCCh. 3.1 - Prob. 8CAVCCh. 3.1 - Plot the given point in a rectangular coordinate...Ch. 3.1 - Prob. 2ES
Ch. 3.1 - Prob. 3ESCh. 3.1 - Prob. 4ESCh. 3.1 - Prob. 5ESCh. 3.1 - Prob. 6ESCh. 3.1 - Prob. 7ESCh. 3.1 - Prob. 8ESCh. 3.1 - Prob. 9ESCh. 3.1 - Prob. 10ESCh. 3.1 - Prob. 11ESCh. 3.1 - 12. Plot the given point in a rectangular...Ch. 3.1 - Prob. 13ESCh. 3.1 - Prob. 14ESCh. 3.1 - Prob. 15ESCh. 3.1 - Prob. 16ESCh. 3.1 - Prob. 17ESCh. 3.1 - Prob. 18ESCh. 3.1 - Prob. 19ESCh. 3.1 - Prob. 20ESCh. 3.1 - Prob. 21ESCh. 3.1 - Prob. 22ESCh. 3.1 - Prob. 23ESCh. 3.1 - Prob. 24ESCh. 3.1 - Prob. 25ESCh. 3.1 - Prob. 26ESCh. 3.1 - Prob. 27ESCh. 3.1 - Prob. 28ESCh. 3.1 - Prob. 29ESCh. 3.1 - Prob. 30ESCh. 3.1 - Prob. 31ESCh. 3.1 - Prob. 32ESCh. 3.1 - Prob. 33ESCh. 3.1 - Prob. 34ESCh. 3.1 - Prob. 35ESCh. 3.1 - Prob. 36ESCh. 3.1 - Prob. 37ESCh. 3.1 - Prob. 38ESCh. 3.1 - Determine whether the ordered pair is a solution...Ch. 3.1 - Prob. 40ESCh. 3.1 - Prob. 41ESCh. 3.1 - Prob. 42ESCh. 3.1 - Prob. 43ESCh. 3.1 - Prob. 44ESCh. 3.1 - Prob. 45ESCh. 3.1 - Prob. 46ESCh. 3.1 - Prob. 47ESCh. 3.1 - Prob. 48ESCh. 3.1 - Prob. 49ESCh. 3.1 - Prob. 50ESCh. 3.1 - Prob. 51ESCh. 3.1 - Prob. 52ESCh. 3.1 - Prob. 53ESCh. 3.1 - Prob. 54ESCh. 3.1 - Prob. 55ESCh. 3.1 - Prob. 56ESCh. 3.1 - Prob. 57ESCh. 3.1 - Prob. 58ESCh. 3.1 - Prob. 59ESCh. 3.1 - Prob. 60ESCh. 3.1 - Prob. 61ESCh. 3.1 - Prob. 62ESCh. 3.1 - Prob. 63ESCh. 3.1 - Prob. 64ESCh. 3.1 - Prob. 65ESCh. 3.1 - Prob. 66ESCh. 3.1 - Prob. 67ESCh. 3.1 - Prob. 68ESCh. 3.1 - Prob. 69ESCh. 3.1 - Prob. 70ESCh. 3.1 - Prob. 71ESCh. 3.1 - Prob. 72ESCh. 3.1 - Prob. 73ESCh. 3.1 - Prob. 74ESCh. 3.1 - Prob. 75ESCh. 3.1 - Prob. 76ESCh. 3.1 - Prob. 77ESCh. 3.1 - Prob. 78ESCh. 3.1 - Prob. 79ESCh. 3.1 - Prob. 80ESCh. 3.1 - Prob. 81ESCh. 3.1 - Prob. 82ESCh. 3.1 - Prob. 83ESCh. 3.1 - Prob. 84ESCh. 3.1 - At the beginning of a semester, a student...Ch. 3.1 - Prob. 86ESCh. 3.1 - Prob. 87ESCh. 3.1 - Prob. 88ESCh. 3.1 - Prob. 89ESCh. 3.1 - Prob. 90ESCh. 3.1 - Prob. 91ESCh. 3.1 - Prob. 92ESCh. 3.1 - Prob. 93ESCh. 3.1 - Prob. 94ESCh. 3.1 - Prob. 95ESCh. 3.1 - Prob. 96ESCh. 3.1 - Prob. 97ESCh. 3.1 - Prob. 98ESCh. 3.1 - Prob. 99ESCh. 3.1 - Prob. 100ESCh. 3.1 - Prob. 101ESCh. 3.1 - Prob. 102ESCh. 3.1 - Prob. 103ESCh. 3.1 - Prob. 104ESCh. 3.1 - Prob. 105ESCh. 3.1 - Prob. 106ESCh. 3.1 - Prob. 107ESCh. 3.1 - Prob. 108ESCh. 3.1 - Prob. 109ESCh. 3.1 - Prob. 110ESCh. 3.1 - Prob. 111ESCh. 3.1 - Prob. 112ESCh. 3.1 - Prob. 113ESCh. 3.1 - Prob. 114ESCh. 3.1 - Prob. 115ESCh. 3.1 - Prob. 116ESCh. 3.1 - Prob. 117ESCh. 3.1 - Prob. 118ESCh. 3.1 - Prob. 119ESCh. 3.1 - Prob. 120ESCh. 3.1 - Prob. 121ESCh. 3.1 - Prob. 122ESCh. 3.2 - Prob. 1CAVCCh. 3.2 - Prob. 2CAVCCh. 3.2 - Prob. 3CAVCCh. 3.2 - Prob. 4CAVCCh. 3.2 - Prob. 5CAVCCh. 3.2 - Prob. 6CAVCCh. 3.2 - Prob. 7CAVCCh. 3.2 - Prob. 8CAVCCh. 3.2 - Prob. 9CAVCCh. 3.2 - Prob. 1ESCh. 3.2 - Prob. 2ESCh. 3.2 - Prob. 3ESCh. 3.2 - Prob. 4ESCh. 3.2 - Prob. 5ESCh. 3.2 - Prob. 6ESCh. 3.2 - Prob. 7ESCh. 3.2 - Prob. 8ESCh. 3.2 - Prob. 9ESCh. 3.2 - Prob. 10ESCh. 3.2 - Prob. 11ESCh. 3.2 - Prob. 12ESCh. 3.2 - Prob. 13ESCh. 3.2 - Prob. 14ESCh. 3.2 - Prob. 15ESCh. 3.2 - Prob. 16ESCh. 3.2 - Prob. 17ESCh. 3.2 - Prob. 18ESCh. 3.2 - Prob. 19ESCh. 3.2 - Prob. 20ESCh. 3.2 - Prob. 21ESCh. 3.2 - Prob. 22ESCh. 3.2 - Prob. 23ESCh. 3.2 - Prob. 24ESCh. 3.2 - Prob. 25ESCh. 3.2 - Prob. 26ESCh. 3.2 - Prob. 27ESCh. 3.2 - Prob. 28ESCh. 3.2 - Prob. 29ESCh. 3.2 - Prob. 30ESCh. 3.2 - Prob. 31ESCh. 3.2 - Prob. 32ESCh. 3.2 - Prob. 33ESCh. 3.2 - Prob. 34ESCh. 3.2 - Prob. 35ESCh. 3.2 - Prob. 36ESCh. 3.2 - Prob. 37ESCh. 3.2 - Prob. 38ESCh. 3.2 - Prob. 39ESCh. 3.2 - Prob. 40ESCh. 3.2 - Prob. 41ESCh. 3.2 - Prob. 42ESCh. 3.2 - Prob. 43ESCh. 3.2 - Prob. 44ESCh. 3.2 - Prob. 45ESCh. 3.2 - Prob. 46ESCh. 3.2 - Prob. 47ESCh. 3.2 - Prob. 48ESCh. 3.2 - Prob. 49ESCh. 3.2 - Prob. 50ESCh. 3.2 - Prob. 51ESCh. 3.2 - Prob. 52ESCh. 3.2 - Prob. 53ESCh. 3.2 - Prob. 54ESCh. 3.2 - Prob. 55ESCh. 3.2 - Prob. 56ESCh. 3.2 - Prob. 57ESCh. 3.2 - Prob. 58ESCh. 3.2 - Prob. 59ESCh. 3.2 - Prob. 60ESCh. 3.2 - Prob. 61ESCh. 3.2 - Prob. 62ESCh. 3.2 - Prob. 63ESCh. 3.2 - Prob. 64ESCh. 3.2 - Prob. 65ESCh. 3.2 - Prob. 66ESCh. 3.2 - Prob. 67ESCh. 3.2 - Prob. 68ESCh. 3.2 - Prob. 69ESCh. 3.2 - Prob. 70ESCh. 3.2 - Prob. 71ESCh. 3.2 - Prob. 72ESCh. 3.2 - Prob. 73ESCh. 3.2 - Prob. 74ESCh. 3.2 - Prob. 75ESCh. 3.2 - Prob. 76ESCh. 3.2 - Prob. 77ESCh. 3.2 - Prob. 78ESCh. 3.2 - Prob. 79ESCh. 3.2 - Prob. 80ESCh. 3.2 - Prob. 81ESCh. 3.2 - Prob. 82ESCh. 3.2 - Prob. 83ESCh. 3.2 - Prob. 84ESCh. 3.2 - Prob. 85ESCh. 3.2 - Prob. 86ESCh. 3.2 - Prob. 87ESCh. 3.2 - Prob. 88ESCh. 3.2 - Prob. 89ESCh. 3.2 - Prob. 90ESCh. 3.2 - Prob. 91ESCh. 3.2 - Prob. 92ESCh. 3.2 - Prob. 93ESCh. 3.2 - Prob. 94ESCh. 3.2 - Prob. 95ESCh. 3.2 - Prob. 96ESCh. 3.2 - Prob. 97ESCh. 3.2 - Prob. 98ESCh. 3.2 - Prob. 99ESCh. 3.2 - Prob. 100ESCh. 3.2 - Prob. 101ESCh. 3.2 - Prob. 102ESCh. 3.2 - Prob. 103ESCh. 3.3 - Prob. 1CAVCCh. 3.3 - Prob. 2CAVCCh. 3.3 - Prob. 3CAVCCh. 3.3 - Prob. 4CAVCCh. 3.3 - Prob. 5CAVCCh. 3.3 - Prob. 6CAVCCh. 3.3 - Prob. 7CAVCCh. 3.3 - Prob. 8CAVCCh. 3.3 - Prob. 1ESCh. 3.3 - Prob. 2ESCh. 3.3 - Prob. 3ESCh. 3.3 - Prob. 4ESCh. 3.3 - Prob. 5ESCh. 3.3 - Prob. 6ESCh. 3.3 - Prob. 7ESCh. 3.3 - Prob. 8ESCh. 3.3 - Prob. 9ESCh. 3.3 - Prob. 10ESCh. 3.3 - Prob. 11ESCh. 3.3 - Prob. 12ESCh. 3.3 - Prob. 13ESCh. 3.3 - Prob. 14ESCh. 3.3 - Prob. 15ESCh. 3.3 - Prob. 16ESCh. 3.3 - Prob. 17ESCh. 3.3 - Prob. 18ESCh. 3.3 - Prob. 19ESCh. 3.3 - Prob. 20ESCh. 3.3 - Prob. 21ESCh. 3.3 - Prob. 22ESCh. 3.3 - Prob. 23ESCh. 3.3 - Prob. 24ESCh. 3.3 - Prob. 25ESCh. 3.3 - Prob. 26ESCh. 3.3 - Prob. 27ESCh. 3.3 - Prob. 28ESCh. 3.3 - Prob. 29ESCh. 3.3 - Prob. 30ESCh. 3.3 - Prob. 31ESCh. 3.3 - Prob. 32ESCh. 3.3 - Prob. 33ESCh. 3.3 - Prob. 34ESCh. 3.3 - Prob. 35ESCh. 3.3 - Prob. 36ESCh. 3.3 - Prob. 37ESCh. 3.3 - Prob. 38ESCh. 3.3 - Prob. 39ESCh. 3.3 - Prob. 40ESCh. 3.3 - Prob. 41ESCh. 3.3 - Prob. 42ESCh. 3.3 - Prob. 43ESCh. 3.3 - Prob. 44ESCh. 3.3 - Prob. 45ESCh. 3.3 - Prob. 46ESCh. 3.3 - Prob. 47ESCh. 3.3 - Prob. 48ESCh. 3.3 - Prob. 49ESCh. 3.3 - Prob. 50ESCh. 3.3 - Prob. 51ESCh. 3.3 - Prob. 52ESCh. 3.3 - Prob. 53ESCh. 3.3 - Prob. 54ESCh. 3.3 - If two lines are parallel, describe the...Ch. 3.3 - Prob. 56ESCh. 3.3 - Prob. 57ESCh. 3.3 - Prob. 58ESCh. 3.3 - Make Sense? In Exercises 57-60, determine whether...Ch. 3.3 - Make Sense? In Exercises 57-60, determine whether...Ch. 3.3 - Prob. 61ESCh. 3.3 - Prob. 62ESCh. 3.3 - Prob. 63ESCh. 3.3 - Prob. 64ESCh. 3.3 - Prob. 65ESCh. 3.3 - Prob. 66ESCh. 3.3 - Prob. 67ESCh. 3.3 - Prob. 68ESCh. 3.3 - Prob. 69ESCh. 3.3 - Prob. 70ESCh. 3.3 - Prob. 71ESCh. 3.3 - Prob. 72ESCh. 3.3 - Prob. 73ESCh. 3.3 - Prob. 74ESCh. 3.3 - Prob. 75ESCh. 3.3 - Prob. 76ESCh. 3.3 - Prob. 77ESCh. 3.4 - Prob. 1CAVCCh. 3.4 - Prob. 2CAVCCh. 3.4 - Prob. 3CAVCCh. 3.4 - Prob. 1ESCh. 3.4 - Prob. 2ESCh. 3.4 - Prob. 3ESCh. 3.4 - Prob. 4ESCh. 3.4 - Prob. 5ESCh. 3.4 - Prob. 6ESCh. 3.4 - Prob. 7ESCh. 3.4 - Prob. 8ESCh. 3.4 - Prob. 9ESCh. 3.4 - Prob. 10ESCh. 3.4 - Prob. 11ESCh. 3.4 - Prob. 12ESCh. 3.4 - Prob. 13ESCh. 3.4 - Prob. 14ESCh. 3.4 - Prob. 15ESCh. 3.4 - Prob. 16ESCh. 3.4 - Prob. 17ESCh. 3.4 - Prob. 18ESCh. 3.4 - Prob. 19ESCh. 3.4 - Prob. 20ESCh. 3.4 - Prob. 21ESCh. 3.4 - Prob. 22ESCh. 3.4 - Prob. 23ESCh. 3.4 - Prob. 24ESCh. 3.4 - Prob. 25ESCh. 3.4 - Prob. 26ESCh. 3.4 - Prob. 27ESCh. 3.4 - Prob. 28ESCh. 3.4 - Prob. 29ESCh. 3.4 - Prob. 30ESCh. 3.4 - Prob. 31ESCh. 3.4 - Prob. 32ESCh. 3.4 - Prob. 33ESCh. 3.4 - Prob. 34ESCh. 3.4 - Prob. 35ESCh. 3.4 - Prob. 36ESCh. 3.4 - Prob. 37ESCh. 3.4 - Prob. 38ESCh. 3.4 - Prob. 39ESCh. 3.4 - Prob. 40ESCh. 3.4 - Prob. 41ESCh. 3.4 - Prob. 42ESCh. 3.4 - Prob. 43ESCh. 3.4 - Prob. 44ESCh. 3.4 - Prob. 45ESCh. 3.4 - Prob. 46ESCh. 3.4 - Prob. 47ESCh. 3.4 - Prob. 48ESCh. 3.4 - Prob. 49ESCh. 3.4 - Prob. 50ESCh. 3.4 - Prob. 51ESCh. 3.4 - Prob. 52ESCh. 3.4 - Prob. 53ESCh. 3.4 - Prob. 54ESCh. 3.4 - Prob. 55ESCh. 3.4 - Graph both linear equations in the same...Ch. 3.4 - Prob. 57ESCh. 3.4 - Prob. 58ESCh. 3.4 - Prob. 59ESCh. 3.4 - Prob. 60ESCh. 3.4 - Prob. 61ESCh. 3.4 - Prob. 62ESCh. 3.4 - Prob. 63ESCh. 3.4 - Prob. 64ESCh. 3.4 - The bar graph breaks down the U.S. population by...Ch. 3.4 - Prob. 66ESCh. 3.4 - Prob. 67ESCh. 3.4 - Prob. 68ESCh. 3.4 - Prob. 69ESCh. 3.4 - Prob. 70ESCh. 3.4 - Prob. 71ESCh. 3.4 - Prob. 72ESCh. 3.4 - Prob. 73ESCh. 3.4 - Prob. 74ESCh. 3.4 - Prob. 75ESCh. 3.4 - Prob. 76ESCh. 3.4 - Prob. 77ESCh. 3.4 - Prob. 78ESCh. 3.4 - Prob. 79ESCh. 3.4 - Prob. 80ESCh. 3.4 - Prob. 81ESCh. 3.4 - Prob. 82ESCh. 3.4 - Prob. 83ESCh. 3.4 - Prob. 84ESCh. 3.5 - Prob. 1CAVCCh. 3.5 - Prob. 2CAVCCh. 3.5 - Prob. 3CAVCCh. 3.5 - Prob. 4CAVCCh. 3.5 - Prob. 5CAVCCh. 3.5 - Prob. 6CAVCCh. 3.5 - Prob. 7CAVCCh. 3.5 - Prob. 8CAVCCh. 3.5 - Prob. 1ESCh. 3.5 - Prob. 2ESCh. 3.5 - Prob. 3ESCh. 3.5 - Prob. 4ESCh. 3.5 - Prob. 5ESCh. 3.5 - Prob. 6ESCh. 3.5 - Prob. 7ESCh. 3.5 - Prob. 8ESCh. 3.5 - Prob. 9ESCh. 3.5 - Prob. 10ESCh. 3.5 - Prob. 11ESCh. 3.5 - Prob. 12ESCh. 3.5 - Prob. 13ESCh. 3.5 - Prob. 14ESCh. 3.5 - Prob. 15ESCh. 3.5 - Prob. 16ESCh. 3.5 - Prob. 17ESCh. 3.5 - Prob. 18ESCh. 3.5 - Prob. 19ESCh. 3.5 - Prob. 20ESCh. 3.5 - Prob. 21ESCh. 3.5 - Prob. 22ESCh. 3.5 - Prob. 23ESCh. 3.5 - Prob. 24ESCh. 3.5 - Prob. 25ESCh. 3.5 - Prob. 26ESCh. 3.5 - Prob. 27ESCh. 3.5 - Prob. 28ESCh. 3.5 - Prob. 29ESCh. 3.5 - Prob. 30ESCh. 3.5 - Prob. 31ESCh. 3.5 - Prob. 32ESCh. 3.5 - Prob. 33ESCh. 3.5 - Prob. 34ESCh. 3.5 - Prob. 35ESCh. 3.5 - Prob. 36ESCh. 3.5 - Prob. 37ESCh. 3.5 - Prob. 38ESCh. 3.5 - Prob. 39ESCh. 3.5 - Prob. 40ESCh. 3.5 - Prob. 41ESCh. 3.5 - Prob. 42ESCh. 3.5 - Prob. 43ESCh. 3.5 - Prob. 44ESCh. 3.5 - Prob. 45ESCh. 3.5 - Prob. 46ESCh. 3.5 - Prob. 47ESCh. 3.5 - Prob. 48ESCh. 3.5 - Prob. 49ESCh. 3.5 - Prob. 50ESCh. 3.5 - Prob. 51ESCh. 3.5 - Prob. 52ESCh. 3.5 - Prob. 53ESCh. 3.5 - Prob. 54ESCh. 3.5 - Prob. 55ESCh. 3.5 - Prob. 56ESCh. 3.5 - Prob. 57ESCh. 3.5 - Prob. 58ESCh. 3.5 - Prob. 59ESCh. 3.5 - Prob. 60ESCh. 3.5 - Prob. 61ESCh. 3.5 - Prob. 62ESCh. 3.5 - Prob. 63ESCh. 3.5 - Prob. 64ESCh. 3.5 - Prob. 65ESCh. 3.5 - Prob. 66ESCh. 3.5 - Prob. 67ESCh. 3.5 - Prob. 68ESCh. 3.5 - Prob. 69ESCh. 3.5 - Prob. 70ESCh. 3.5 - Prob. 71ESCh. 3.5 - Prob. 72ESCh. 3.5 - Prob. 73ESCh. 3.5 - Prob. 74ESCh. 3.5 - Prob. 75ESCh. 3.5 - Prob. 76ESCh. 3.5 - Prob. 77ESCh. 3.5 - Prob. 78ESCh. 3.5 - Prob. 79ESCh. 3.5 - Prob. 80ESCh. 3.5 - Prob. 81ESCh. 3.5 - Prob. 82ESCh. 3.5 - Prob. 83ESCh. 3.5 - Prob. 84ESCh. 3.5 - Prob. 85ESCh. 3.5 - Prob. 86ESCh. 3.5 - Prob. 87ESCh. 3.5 - Prob. 88ESCh. 3.5 - Prob. 89ESCh. 3 - Prob. 1MCPCh. 3 - Prob. 2MCPCh. 3 - Prob. 3MCPCh. 3 - Prob. 4MCPCh. 3 - Prob. 5MCPCh. 3 - Prob. 6MCPCh. 3 - Prob. 7MCPCh. 3 - Prob. 8MCPCh. 3 - Prob. 9MCPCh. 3 - Prob. 10MCPCh. 3 - Prob. 11MCPCh. 3 - Prob. 12MCPCh. 3 - Prob. 13MCPCh. 3 - Prob. 14MCPCh. 3 - Prob. 15MCPCh. 3 - Prob. 16MCPCh. 3 - Prob. 17MCPCh. 3 - Prob. 18MCPCh. 3 - Prob. 19MCPCh. 3 - Prob. 20MCPCh. 3 - Prob. 1RECh. 3 - Prob. 2RECh. 3 - Prob. 3RECh. 3 - Prob. 4RECh. 3 - Prob. 5RECh. 3 - Prob. 6RECh. 3 - Prob. 7RECh. 3 - Prob. 8RECh. 3 - Prob. 9RECh. 3 - Prob. 10RECh. 3 - Prob. 11RECh. 3 - Prob. 12RECh. 3 - Prob. 13RECh. 3 - Prob. 14RECh. 3 - Prob. 15RECh. 3 - Prob. 16RECh. 3 - Prob. 17RECh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Prob. 20RECh. 3 - Prob. 21RECh. 3 - Prob. 22RECh. 3 - Prob. 23RECh. 3 - Prob. 24RECh. 3 - Calculate the slope of the line passing through...Ch. 3 - Prob. 26RECh. 3 - Prob. 27RECh. 3 - Prob. 28RECh. 3 - Find the slope of given line, or state that the...Ch. 3 - Prob. 30RECh. 3 - Prob. 31RECh. 3 - Prob. 32RECh. 3 - In a 2010 survey of more than 200,000 freshmen at...Ch. 3 - Prob. 34RECh. 3 - Prob. 35RECh. 3 - Prob. 36RECh. 3 - Prob. 37RECh. 3 - Prob. 38RECh. 3 - Prob. 39RECh. 3 - Prob. 40RECh. 3 - Prob. 41RECh. 3 - Prob. 42RECh. 3 - Prob. 43RECh. 3 - Prob. 44RECh. 3 - Prob. 45RECh. 3 - Prob. 46RECh. 3 - Prob. 47RECh. 3 - Prob. 48RECh. 3 - Prob. 49RECh. 3 - Prob. 1TCh. 3 - Prob. 2TCh. 3 - Prob. 3TCh. 3 - Prob. 4TCh. 3 - Prob. 5TCh. 3 - Prob. 6TCh. 3 - Prob. 7TCh. 3 - Prob. 8TCh. 3 - Prob. 9TCh. 3 - Prob. 10TCh. 3 - Prob. 11TCh. 3 - Prob. 12TCh. 3 - Prob. 13TCh. 3 - Prob. 14TCh. 3 - Prob. 15TCh. 3 - Prob. 16TCh. 3 - Prob. 17TCh. 3 - Prob. 18TCh. 3 - Prob. 19TCh. 3 - Prob. 1CRECh. 3 - Prob. 2CRECh. 3 - Prob. 3CRECh. 3 - Prob. 4CRECh. 3 - Prob. 5CRECh. 3 - Prob. 6CRECh. 3 - Prob. 7CRECh. 3 - Prob. 8CRECh. 3 - Prob. 9CRECh. 3 - Prob. 10CRECh. 3 - Prob. 11CRECh. 3 - Prob. 12CRECh. 3 - Prob. 13CRECh. 3 - Prob. 14CRECh. 3 - Prob. 15CRECh. 3 - Prob. 16CRECh. 3 - Prob. 17CRECh. 3 - Prob. 18CRECh. 3 - Prob. 19CRECh. 3 - Prob. 20CRE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- In simplest way, For each quadratic relation, find the zeros and the maximum or minimum. a) y = x 2 + 16 x + 39 b) y = 5 x2 - 50 x - 120arrow_forwardIn simplest terms and step by step Write each quadratic relation in standard form, then fi nd the zeros. y = - 4( x + 6)2 + 36arrow_forwardIn simplest terms and step by step For each quadratic relation, find the zeros and the maximum or minimum. 1) y = - 2 x2 - 28 x + 64 2) y = 6 x2 + 36 x - 42arrow_forward
- Write each relation in standard form a)y = 5(x + 10)2 + 7 b)y = 9(x - 8)2 - 4arrow_forwardIn simplest form and step by step Write the quadratic relation in standard form, then fi nd the zeros. y = 3(x - 1)2 - 147arrow_forwardStep by step instructions The path of a soccer ball can be modelled by the relation h = - 0.1 d 2 + 0.5 d + 0.6, where h is the ball’s height and d is the horizontal distance from the kicker. a) Find the zeros of the relation.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
Points, Lines, Planes, Segments, & Rays - Collinear vs Coplanar Points - Geometry; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=dDWjhRfBsKM;License: Standard YouTube License, CC-BY
Naming Points, Lines, and Planes; Author: Florida PASS Program;https://www.youtube.com/watch?v=F-LxiLSSaLg;License: Standard YouTube License, CC-BY