
Concept explainers
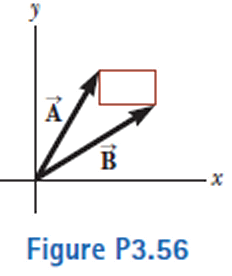
The rectangle shown in Figure P3.56 has sides parallel to the x and y axes. The position vectors of two corners are 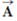 = 10.0 m at 50.0° and
= 10.0 m at 50.0° and 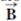 = 12.0 m at 30.0°. (a) Find the perimeter of the rectangle. (b) Find the magnitude and direction of the vector from the origin to the upper-right corner of the rectangle.
= 12.0 m at 30.0°. (a) Find the perimeter of the rectangle. (b) Find the magnitude and direction of the vector from the origin to the upper-right corner of the rectangle.
(a)
The perimeter of the rectangle.
Answer to Problem 3.56AP
The perimeter of the rectangle is
Explanation of Solution
Given info: The rectangle has sides parallel to the
The vector component of
Here,
Substitute
Thus, the vector component of
The vector component of
Here,
Substitute
Thus, the vector component of
The position vector
Here,
Substitute
Thus, the position vector for the vector
The component of vector
Here,
Substitute
Thus, the component of vector
The component of vector
Here,
Substitute
Thus, the component of vector
The position vector of the vector
Here,
Substitute
Thus, the position vector of the vector
The length of the rectangle is,
Here,
The width of the rectangle is,
Here,
The vector
Substitute
Formula to calculate the perimeter of the rectangle is,
Here,
Substitute
Conclusion:
Therefore, the perimeter of the rectangle is
(b)
The magnitude and direction of the vector from the origin to the upper right coordinate of the rectangle.
Answer to Problem 3.56AP
The magnitude and direction of the vector from the origin to the upper right coordinate of the rectangle is
Explanation of Solution
Given info: The rectangle has sides parallel to the
The vector of point
The vector
Here,
Substitute
Formula to calculate the magnitude of vector
Here,
Substitute
Formula to calculate the angle made by the vector
Here,
Substitute
Conclusion:
Therefore, the magnitude and direction of the vector from the origin to the upper right coordinate of the rectangle is
Want to see more full solutions like this?
Chapter 3 Solutions
Physics for Scientists and Engineers
Additional Science Textbook Solutions
Organic Chemistry
Microbiology Fundamentals: A Clinical Approach
Human Physiology: An Integrated Approach (8th Edition)
Fundamentals Of Thermodynamics
Anatomy & Physiology (6th Edition)
Principles of Anatomy and Physiology
- please answer this asap!!!!arrow_forwardRT = 4.7E-30 18V IT = 2.3E-3A+ 12 38Ω ли 56Ω ли r5 27Ω ли r3 28Ω r4 > 75Ω r6 600 0.343V 75.8A Now figure out how much current in going through the r4 resistor. |4 = unit And then use that current to find the voltage drop across the r resistor. V4 = unitarrow_forward7 Find the volume inside the cone z² = x²+y², above the (x, y) plane, and between the spheres x²+y²+z² = 1 and x² + y²+z² = 4. Hint: use spherical polar coordinates.arrow_forward
- ганм Two long, straight wires are oriented perpendicular to the page, as shown in the figure(Figure 1). The current in one wire is I₁ = 3.0 A, pointing into the page, and the current in the other wire is 12 4.0 A, pointing out of the page. = Find the magnitude and direction of the net magnetic field at point P. Express your answer using two significant figures. VO ΜΕ ΑΣΦ ? Figure P 5.0 cm 5.0 cm ₁ = 3.0 A 12 = 4.0 A B: μΤ You have already submitted this answer. Enter a new answer. No credit lost. Try again. Submit Previous Answers Request Answer 1 of 1 Part B X Express your answer using two significant figures. ΜΕ ΑΣΦ 0 = 0 ? below the dashed line to the right P You have already submitted this answer. Enter a new answer. No credit lost. Try again.arrow_forwardAn infinitely long conducting cylindrical rod with a positive charge λ per unit length is surrounded by a conducting cylindrical shell (which is also infinitely long) with a charge per unit length of −2λ and radius r1, as shown in the figure. What is σinner, the surface charge density (charge per unit area) on the inner surface of the conducting shell? What is σouter, the surface charge density on the outside of the conducting shell? (Recall from the problem statement that the conducting shell has a total charge per unit length given by −2λ.)arrow_forwardA small conducting spherical shell with inner radius aa and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d (Figure 1). The inner shell has total charge +2q, and the outer shell has charge −2q. What's the total charge on the inner surface of the small shell? What's the total charge on the outer surface of the small shell? What's the total charge on the inner surface of the large shell? What's the total charge on the outer surface of the large shell?arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





