Chapter 3, Problem 3.37P

(a)

To determine

Sketch a diagram to illustrate the equation $r_{\alpha }=r_{\alpha }-R$.

Answer to Problem 3.37P

Figure $1$ shows the diagram to illustrate the equation $r_{\alpha }=r_{\alpha }-R$.

Explanation of Solution

Consider a system of $N$ number of masses each of mass $m_{\alpha }$ and the position of each mass with respective to the origin is $r_{\alpha }$. If the position of a particle with respective to the center of mass is ${r^{\prime }}_{\alpha }$ and the position of center of mass with respective to the origin is $R$.

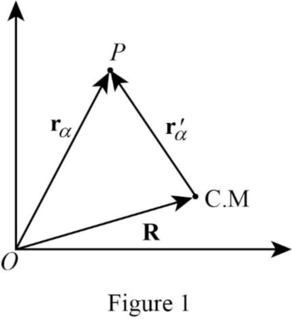
Figure $1$ shows the diagram to illustrate the equation $r_{\alpha }=r_{\alpha }-R$.

In figure $1$, center of mass represents the point of center of mass of the system of particles and $P$ represents the point of any mass in the system.

Use figure $1$ and write the concept of addition of vectors.

    ${r^{\prime }}_{\alpha }+R=r_{\alpha }$        (I)

Use equation (I) to solve for ${r^{\prime }}_{\alpha }$.

    ${r^{\prime }}_{\alpha }=r_{\alpha }-R$        (II)

Conclusion:

Therefore, figure $1$ shows the diagram to illustrate the equation $r_{\alpha }=r_{\alpha }-R$.

(b)

To determine

Prove the relation ${\displaystyle \sum m_{\alpha }{r^{\prime }}_{\alpha }}=0$.

Answer to Problem 3.37P

It is proved that the relation ${\displaystyle \sum m_{\alpha }{r^{\prime }}_{\alpha }}=0$.

Explanation of Solution

Write the expression for the sum of moment of masses about the center of mass.

    $\begin{array}{c}{\displaystyle \sum _{\alpha =1}^N{m}_{\alpha }{r^{\prime }}_{\alpha }}={\displaystyle \sum _{\alpha =1}^N{m}_{\alpha }\left(r_{\alpha }-R\right)}\\ ={\displaystyle \sum _{\alpha =1}^N{m}_{\alpha }{r}_{\alpha }}-{\displaystyle \sum _{\alpha =1}^N{m}_{\alpha }R}\\ ={\displaystyle \sum _{\alpha =1}^N{m}_{\alpha }{r}_{\alpha }}-R{\displaystyle \sum _{\alpha =1}^N{m}_{\alpha }}\end{array}$        (III)

Write the expression for the position of the center of mass of $N$ masses in a system.

    $\begin{array}{c}R=\frac{1}{M}{\displaystyle \sum _{\alpha =1}^N{m}_{\alpha }{r}_{\alpha }}\\ {\displaystyle \sum _{\alpha =1}^N{m}_{\alpha }{r}_{\alpha }}=MR\end{array}$        (IV)

Write the expression for the mass of all the particles in the system.

    $M={\displaystyle \sum _{\alpha =1}^N{m}_{\alpha }}$        (V)

Use equation (IV) and (V) in (III) to solve for the sum of moment of masses about the center of mass.

    $\begin{array}{c}{\displaystyle \sum _{\alpha =1}^N{m}_{\alpha }{r}_{\alpha }}=MR-MR\left(M\right)\\ =0\\ {\displaystyle \sum _{\alpha =1}^N{m}_{\alpha }{r}_{\alpha }}=0\end{array}$        (VI)

The sum $\left(\frac{1}{M}\right){\displaystyle \sum _{\alpha =1}^N{m}_{\alpha }{r}_{\alpha }}$ defines the position of the center of mass relative to the origin.

Conclusion:

Therefore, it is proved that the relation ${\displaystyle \sum m_{\alpha }{r^{\prime }}_{\alpha }}=0$.

(c)

To determine

Prove the rate of change of the angular momentum about the center of mass is equal to the total external torque about the center of mass.

Answer to Problem 3.37P

It is proved that the rate of change of the angular momentum about the center of mass is equal to the total external torque about the center of mass.

Explanation of Solution

Write the expression for the angular momentum of the system about the center of mass.

    $L={\displaystyle \sum _{\alpha =1}^N{r^{\prime }}_{\alpha }\times {p^{\prime }}_{\alpha }}$        (VII)

Here, $L$ is the angular momentum, ${p^{\prime }}_{\alpha }$ is the linear momentum.

Write the expression for momentum.

    $p=m\dot{r}$        (VIII)

Here, $\dot{r}$ .is the rate of change of position.

Use equation (VIII) in (VII) to solve for $L$.

    $L={\displaystyle \sum _{\alpha =1}^N{r^{\prime }}_{\alpha }\times \left(m_{\alpha }{{\dot{r}}^{\prime }}_{\alpha }\right)}$        (IX)

Differentiate equate (IX) with respect to time on both sides,

    $\dot{L}={\displaystyle \sum _{\alpha =1}^N{\dot{r^{\prime }}}_{\alpha }\times \left(m_{\alpha }{{\dot{r}}^{\prime }}_{\alpha }\right)}+{\displaystyle \sum _{\alpha =1}^N{r^{\prime }}_{\alpha }\times \left(m_{\alpha }{\ddot{r^{\prime }}}_{\alpha }\right)}$        (X)

Take the $\frac{d^2}{d{t}^2}$ of the equation (II),

    ${{\ddot{r}}^{\prime }}_{\alpha }={\ddot{r}}_{\alpha }-\ddot{R}$        (XI)

Use equation (XI) in (X) to solve for $L$.

    $\begin{array}{c}\dot{L}={\displaystyle \sum _{\alpha =1}^N{m}_{\alpha }{\dot{r^{\prime }}}_{\alpha }\times {\dot{r^{\prime }}}_{\alpha }}+{\displaystyle \sum _{\alpha =1}^N{r^{\prime }}_{\alpha }\times m_{\alpha }{{\ddot{r}}^{\prime }}_{\alpha }}\\ =0+{\displaystyle \sum _{\alpha =1}^N{r^{\prime }}_{\alpha }\times m_{\alpha }\left({\ddot{r}}_{\alpha }-\ddot{R}\right)}\\ ={\displaystyle \sum _{\alpha =1}^N{r^{\prime }}_{\alpha }\times m_{\alpha }{\ddot{r}}_{\alpha }}-{\displaystyle \sum _{\alpha =1}^N{r^{\prime }}_{\alpha }\times m_{\alpha }\ddot{R}}\\ ={\displaystyle \sum _{\alpha =1}^N{r^{\prime }}_{\alpha }\times m_{\alpha }{\ddot{r}}_{\alpha }}-{\displaystyle \sum _{\alpha =1}^N{m}_{\alpha }{r^{\prime }}_{\alpha }\times \ddot{R}}\end{array}$        (XII)

Write the expression for the external force acting on a mass  $m_{\alpha }$.

    $F^{\text{ext}}=m_{\alpha }{\ddot{r}}_{\alpha }$        (XIII)

Here, $F^{\text{ext}}$ is the external force, $\ddot{r}$ is the acceleration.

Write the expression for the torque acting on mass $m_{\alpha }$ is about center of mass.

    ${\left({\tau }^{\text{ext}}\right)}_{\alpha }={r^{\prime }}_{\alpha }\times F^{\text{ext}}$        (XIV)

Write the expression for ${\displaystyle \sum _{\alpha =1}^N{m}_{\alpha }{r^{\prime }}_{\alpha }}$.

    ${\displaystyle \sum _{\alpha =1}^N{m}_{\alpha }{r^{\prime }}_{\alpha }}=0$        (XV)

Use equation (XV), (XIV) and (XIII) in (XII) to solve for $\dot{L}$.

    $\begin{array}{c}\dot{L}={\displaystyle \sum _{\alpha =1}^N{r^{\prime }}_{\alpha }\times F^{\text{ext}}-0}\\ ={\left({\tau }^{\text{ext}}\right)}_{\alpha }\end{array}$        (XVI)

Sum of external torque acting on each mass of the system is equal to the external torque acting on the system about its center of mass.

    $\dot{L}={\tau }^{\text{ext}}$        (XVII)

Here, ${\tau }^{\text{ext}}$ is the external torque acting on the system about its center of mass.

Conclusion:

Therefore, it is proved that the rate of change of the angular momentum about the center of mass is equal to the total external torque about the center of mass.