
Concept explainers
(a)
The measurement of a.
Answer to Problem 7A
The measurement of a is (332)′′.
Explanation of Solution
Given information:
The below figure represent the Metric steel Rule.
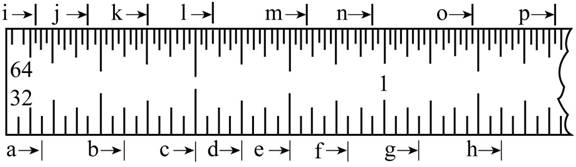
Figure-(1)
Write the expression for the measurement by the enlarged fractional rule.
M=F+T(132)′′ ........ (I)
Here, the measurement by the enlarged fractional rule is M, the total measurement of scale nearest of the point is F and the fractional measurement of scale nearest of the point is T.
Here, the total measurement of scale nearest of a is 0 and the fractional measurement of scale nearest of a is 3 as shown in Figure-(1).
Calculation:
Substitute 3 for T and 0 for F in Equation (I).
M=0+(3)(132)′′=(3)(132)′′=(332)′′
Conclusion:
The measurement of a is (332)′′.
(b)
The measurement of b.
Answer to Problem 7A
The measurement of b is (516)′′.
Explanation of Solution
Given information:
Here, the total measurement of scale nearest of b is 0 and the fractional measurement of scale nearest of b is 10 as shown in Figure-(1).
Calculation:
Substitute 0 for T and 10 for F in Equation (I).
M=(0)+(10)(132)′′=(10)(132)′′=(516)′′
Conclusion:
The measurement of b is (516)′′.
(c)
The measurement of c.
Answer to Problem 7A
The measurement of c is 0.5″.
Explanation of Solution
Given information:
Here, the total measurement of scale nearest of c is 0 and the fractional measurement of scale nearest of c is 16 as shown in Figure-(1).
Calculation:
Substitute 0 for T and 16 for F in Equation (I).
M=(0)+(16)(132)′′=(16)(132)′′=(12)′′=0.5″
Conclusion:
The measurement of c is 0.5′′.
(d)
The measurement of d.
Answer to Problem 7A
The measurement of d is (58)′′.
Explanation of Solution
Given information:
Here, the total measurement of scale nearest of d is 0.5″ and the fractional measurement of scale nearest of d is 4 as shown in Figure-(1).
Calculation:
Substitute 0.5″ for T and 4 for F in Equation (I).
M=0.5″+(4)(132)′′=(12)′′+(18)′′=(58)′′
Conclusion:
The measurement of d is (58)′′.
(e)
The measurement of e.
Answer to Problem 7A
The measurement of e is (34)′′.
Explanation of Solution
Given information:
Here, the total measurement of scale nearest of e is 0.5″ and the fractional measurement of scale nearest of e is 8 as shown in Figure-(1).
Calculation:
Substitute 0.5″ for T and 8 for F in Equation (I).
M=(0.5″)+(8)(132)′′=(12)′′+(14)′′=(34)′′
Conclusion:
The measurement of e is (34)′′.
(f)
The measurement of f.
Answer to Problem 7A
The measurement of f is (2932)′′.
Explanation of Solution
Given information:
Here, the total measurement of scale nearest of f is 0.5″ and the fractional measurement of scale nearest of f is 13 as shown in Figure-(1).
Calculation:
Substitute 0.5″ for T and 13 for F in Equation (I).
M=(0.5″)+(13)(132)′′=(12)′′+(1332)′′=(2932)′′
Conclusion:
The measurement of f is (2932)′′.
(g)
The measurement of g.
Answer to Problem 7A
The measurement of g is (3532)′′.
Explanation of Solution
Given information:
Here, the total measurement of scale nearest of g is 1″ and the fractional measurement of scale nearest of g is 3 as shown in Figure-(1).
Calculation:
Substitute 1″ for T and 3 for F in Equation (I).
M=(1″)+(3)(132)′′=(1″)+(332)′′=(3532)′′
Conclusion:
The measurement of g is (3532)′′.
(h)
The measurement of h.
Answer to Problem 7A
The measurement of h is (2116)′′.
Explanation of Solution
Given information:
Here, the total measurement of scale nearest of h is 1″ and the fractional measurement of scale nearest of h is 10 as shown in Figure-(1).
Calculation:
Substitute 1″ for T and 10 for F in Equation (I).
M=(1″)+(10)(132)′′=(1″)+(516)′′=(2116)′′
Conclusion:
The measurement of h is (2116)′′.
(i)
The measurement of i.
Answer to Problem 7A
The measurement of i is (564)′′.
Explanation of Solution
Given information:
Write the expression of measurement of the enlarged decimal rule.
M=F(132)′′+T(164)′′ ........ (II)
Here, the total measurement of scale nearest of i is 2 and the fractional measurement of scale nearest of i is 1 as shown in Figure-(1).
Calculation:
Substitute 2 for F and 1 for T in Equation (II).
M=2(132)′′+(164)′′=(16)′′+(164)′′=(564)′′
Conclusion:
The measurement of i is (564)′′.
(j)
The measurement of j.
Answer to Problem 7A
The measurement of j is (732)′′.
Explanation of Solution
Given information:
Here, the total measurement of scale nearest of j is 6 and the fractional measurement of scale nearest of c is 2 as shown in Figure-(1).
Calculation:
Substitute 6 for F and 2 for T in Equation (II).
M=(6)(132)′′+(2)(164)′′=(316)′′+(132)′′=(732)′′
Conclusion:
The measurement of j is (732)′′.
(k)
The measurement of k.
Answer to Problem 7A
The measurement of k is (38)′′.
Explanation of Solution
Given information:
Here, the total measurement of scale nearest of k is 0 and the fractional measurement of scale nearest of k is 12 as shown in Figure-(1).
Calculation:
Substitute 0 for T and 12 for F in Equation (I).
M=(0)+(12)(132)′′=(38)′′
Conclusion:
The measurement of k is (38)′′.
(l)
The measurement of l.
Answer to Problem 7A
The measurement of l is (3564)′′.
Explanation of Solution
Given information:
Here, the total measurement of scale nearest of l is 5 and the fractional measurement of scale nearest of l is 1 as shown in Figure-(1).
Write the expression for the enlarged decimal rule.
M=T1+F(132)′′+T(164)′′ ...... (III)
Here, the total measurement is T1.
Calculation:
Substitute (38)′′ for T1, 5 for F and 1 for T in Equation (II).
M=(38)′′+5(132)′′+(1)(164)′′=(38)′′+(532)′′+(164)′′=(3564)′′
Conclusion:
The measurement of l is (3564)′′.
(m)
The measurement of m.
Answer to Problem 7A
The measurement of m is (5164)′′.
Explanation of Solution
Given information:
Here, the total measurement of scale nearest of m is 24 and the fractional measurement of scale nearest of m is 3 as shown in Figure-(1).
Calculation:
Substitute 24 for F and 3 for T in Equation (I).
M=(24)(132)′′+(3)(164)′′=(5164)′′
Conclusion:
The measurement of m is (5164)′′.
(n)
The measurement of n.
Answer to Problem 7A
The measurement of n is (3132)′′.
Explanation of Solution
Given information:
Write the expression of measurement of the enlarged decimal rule.
M=T1−T(164)′′ ........ (IV)
Here, the total measurement is T1.
Here, the fractional measurement of scale nearest of n is 2 and the total measurement is 1″ as shown in Figure-(1).
Calculation:
Substitute 1″ for T1 and 2 for T in Equation (IV).
M=(1″)−2(164)′′=(1″)−(132)′′=(3132)′′
Conclusion:
The measurement of n is (3132)′′.
(o)
The measurement of o.
Answer to Problem 7A
The measurement of o is (11564)′′.
Explanation of Solution
Given information:
Here, the total measurement of scale nearest of m is 7, the fractional measurement of scale nearest of m is 1 and the total measurement is 1″ as shown in Figure-(1).
Calculation:
Substitute 1″ for T1, 7 for F and 1 for T in Equation (III).
M=(1″)+(7)(132)′′+(1)(164)′′=(1″)+(732)′′+(164)′′=(11564)′′
Conclusion:
The measurement of o is (11564)′′.
(o)
The measurement of p.
Answer to Problem 7A
The measurement of p is (12964)′′.
Explanation of Solution
Given information:
Here, the total measurement of scale nearest of m is 4, the fractional measurement of scale nearest of m is 1 and the total measurement is (2116)′′ as shown in Figure-(1).
Calculation:
Substitute (2116)′′ for T1, 4 for F and 1 for F in Equation (IV).
M=(2116)′′+(4)(132)′′+(1)(164)′′=(2116)′′+(18)′′+(164)′′=(2964)′′
Conclusion:
The measurement of p is (12964)′′.
Want to see more full solutions like this?
Chapter 28 Solutions
EBK MATHEMATICS FOR MACHINE TECHNOLOGY
- Problems Construct shear and moment diagrams using the equilib- rium method. Indicate the magnitudes of Vmax and Mmax. 7.3 107 B 5' 201arrow_forwardCan you help me with this problem using linear recurrance: Find an explicit formula for the recurrence relation an = 2can−1 + 3c2an−2 where c not equal to 0 with initial conditions a0=4c and a1 = 0arrow_forwardCan you help me solved this problem using generalized combination:How many combinations are there to pick r objects from 2n objects numbered from 1to 2n when repetitions are allowed and at least one object of odd type does not appear?arrow_forward
- In Exercises 1-14, state whether each statement is true or false. If false, give a reason. 1. The set of stores located in the state of Wyoming is a well- defined set. 2. The set of the three best songs is a well-defined set. 3. maple = {oak, elm, maple, sycamore} 4{} cơ 5. {3, 6, 9, 12,...} and {2, 4, 6, 8, ...} are disjoint sets. 6. {Mercury, Venus, Earth, Mars} is an example of a set in roster form. 7. {candle, picture, lamp} = {picture, chair, lamp } 8. {apple, orange, banana, pear} is equivalent to {tomato, corn, spinach, radish}.arrow_forwardExercises Evaluate the following limits. 1. lim cot x/ln x +01x 2. lim x² In x +014 3. lim x* x0+ 4. lim (cos√√x)1/x +014 5. lim x2/(1-cos x) x10 6. lim e*/* 818 7. lim (secx - tan x) x-x/2- 8. lim [1+(3/x)]* x→∞0arrow_forwardIn Exercises 1 through 3, let xo = O and calculate P7(x) and R7(x). 1. f(x)=sin x, x in R. 2. f(x) = cos x, x in R. 3. f(x) = In(1+x), x≥0. 4. In Exercises 1, 2, and 3, for |x| 1, calculate a value of n such that P(x) approximates f(x) to within 10-6. 5. Let (an)neN be a sequence of positive real numbers such that L = lim (an+1/an) exists in R. If L < 1, show that an → 0. [Hint: Let 1111 Larrow_forward
- iation 7. Let f be continuous on [a, b] and differentiable on (a, b). If lim f'(x) xia exists in R, show that f is differentiable at a and f'(a) = lim f'(x). A similar result holds for b. x-a 8. In reference to Corollary 5.4, give an example of a uniformly continuous function on [0, 1] that is differentiable on (0, 1] but whose derivative is not bounded there. 9. Recall that a fixed point of a function f is a point c such that f(c) = c. (a) Show that if f is differentiable on R and f'(x)| x if x 1 and hence In(1+x) 0. 12. For 0 л/2. (Thus, as x л/2 from the left, cos x is never large enough for x+cosx to be greater than л/2 and cot x is never small enough for x + cot x to be less than x/2.)arrow_forward1. Show that f(x) = x3 is not uniformly continuous on R. 2. Show that f(x) = 1/(x-2) is not uniformly continuous on (2,00). 3. Show that f(x)=sin(1/x) is not uniformly continuous on (0,л/2]. 4. Show that f(x) = mx + b is uniformly continuous on R. 5. Show that f(x) = 1/x2 is uniformly continuous on [1, 00), but not on (0, 1]. 6. Show that if f is uniformly continuous on [a, b] and uniformly continuous on D (where D is either [b, c] or [b, 00)), then f is uniformly continuous on [a, b]U D. 7. Show that f(x)=√x is uniformly continuous on [1, 00). Use Exercise 6 to conclude that f is uniformly continuous on [0, ∞). 8. Show that if D is bounded and f is uniformly continuous on D, then fis bounded on D. 9. Let f and g be uniformly continuous on D. Show that f+g is uniformly continuous on D. Show, by example, that fg need not be uniformly con- tinuous on D. 10. Complete the proof of Theorem 4.7. 11. Give an example of a continuous function on Q that cannot be continuously extended to R. 12.…arrow_forwardcan I see the steps for how you got the same answers already provided for μ1->μ4. this is a homework that provide you answers for question after attempting it three triesarrow_forward
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw HillAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw HillAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell





