Linear Algebra And Its Applications
6th Edition
ISBN: 9780135851258
Author: Lay, David C., Steven R., MCDONALD, Judith
Publisher: Pearson,
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 2.8, Problem 4E
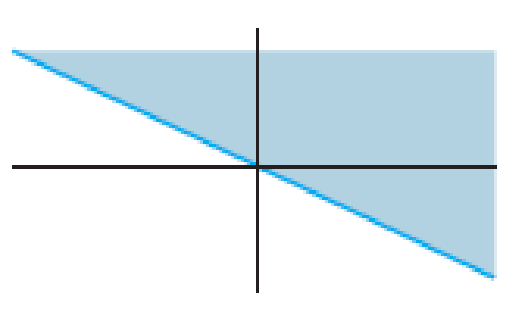
Exercises 1-4 display sets in ℝ2. Assume the sets include the bounding lines. In each case, give a specific reason why the set H is not a subspace of ℝ2. (For instance, find two
4. 
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
5) You are purchasing a game for $30. You have a 5% off coupon and sales tax is 5%. What
will your final price be? Does it matter if you take off the coupon first or add in the tax first?
6) You have ten coupons that allow you to take 10% off the sales price of a jacket, and for
some strange reason, the store is going to allow you to use all ten coupons! Does this mean
you get the jacket for free? Let's really think about what would happen at the checkout.
First, the teller would scan the price tag on the jacket, and the computer would show the
price is $100. After the teller scans the first coupon, the computer will take 10% off of
$100, and show the price is $90. (Right? Think about why this is.) Then after the teller scans
the second coupon, the computer will take 10% off of $90.
(a) Continue this reasoning to fill in the table below showing the price of the jacket (y) after
you apply x coupons.
(b) Make a graph showing the price of the jacket from x = 0 to x = 10 coupons applied.…
(a)
(b)
(c)
(d)
de
unique?
Answer the following questions related to the linear system
x + y + z = 2
x-y+z=0
2x + y 2 3
rewrite the linear system into the matrix-vector form A = 5
Fuse elementary row operation to solve this linear system. Is the solution
use elementary row operation to find the inverse of A and then solve
the linear system. Verify the solution is the same as (b).
give the null space of matrix A and find the dimension of null space.
give the column space of matrix A and find the dimension of the column
space of A (Hint: use Rank-Nullity Theorem).
please explain in a clear way
Chapter 2 Solutions
Linear Algebra And Its Applications
Ch. 2.1 - Since vectors in n may be regarded as n 1...Ch. 2.1 - Let A be a 4 4 matrix and let x be a vector in 4....Ch. 2.1 - Suppose A is an m n matrix, all of whose rows are...Ch. 2.1 - If a matrix A is 5 3 and the product AB is 5 7,...Ch. 2.1 - How many rows does B have if BC is a 3 4 matrix?Ch. 2.1 - Let A=[2531] and B=[453k]. What value(s) of k, if...Ch. 2.1 - Let A=[2346], B=[8455], and C=[5231]. Verify that...Ch. 2.1 - Let A=[111123145] and D=[200030005]. Compute AD...Ch. 2.1 - Let A=[3612]. Construct a 2 2 matrix B such that...Ch. 2.1 - Let r1,..., rp be vectors in n, and let Q be an m ...
Ch. 2.1 - Let U be the 3 2 cost matrix described in Example...Ch. 2.1 - If A=[1225] and AB=[121693], determine the first...Ch. 2.1 - Suppose the first two columns, b1 and b2, of B are...Ch. 2.1 - Suppose die third column of B is die sum of die...Ch. 2.1 - Suppose the second column of B is all zeros. What...Ch. 2.1 - Suppose the last column of AB is entirely zero but...Ch. 2.1 - Show that if the columns of B are linearly...Ch. 2.1 - Suppose CA = In (the n n identity matrix). Show...Ch. 2.1 - Suppose AD = Im (the m m identity matrix). Show...Ch. 2.1 - Suppose A is an m n matrix and there exist n m...Ch. 2.1 - Suppose A is a 3 n matrix whose columns span 3....Ch. 2.1 - In Exercises 27 and 28, view vectors in n as n 1...Ch. 2.1 - If u and v are in n. how are uTv and vTu related?...Ch. 2.1 - Prove Theorem 2(b) and 2(c). Use the row-column...Ch. 2.1 - Prove Theorem 2(d). [Hint: The (i, j)-entry in...Ch. 2.1 - Show that ImA = A when A is an m n matrix. You...Ch. 2.1 - Show that AIn = A when A is an m n matrix. [Hint:...Ch. 2.1 - Prove Theorem 3(d). [Hint: Consider the jth row of...Ch. 2.1 - Give a formula for (A Bx)T, where x is a vector...Ch. 2.2 - Use determinants to determine which of the...Ch. 2.2 - Find the inverse of the matrix A = [121156545], if...Ch. 2.2 - If A is an invertible matrix, prove that 5A is an...Ch. 2.2 - Prob. 7ECh. 2.2 - Prob. 8ECh. 2.2 - Let A = [12512], b1 = [13], b2 = [15], b3 = [26],...Ch. 2.2 - Use matrix algebra to show that if A is invertible...Ch. 2.2 - Let A be an invertible n n matrix, and let B be...Ch. 2.2 - Let A be an invertible n n matrix, and let B be...Ch. 2.2 - Suppose AB = AC. where B and C are n p matrices...Ch. 2.2 - Suppose (B C) D = 0, where B and C are m n...Ch. 2.2 - Suppose A, B, and C are invertible n n matrices....Ch. 2.2 - Suppose A and B are n n, B is invertible, and AB...Ch. 2.2 - Solve the equation AB = BC for A, assuming that A,...Ch. 2.2 - Suppose P is invertible and A = PBP1 Solve for B...Ch. 2.2 - If A, B, and C are n n invertible matrices, does...Ch. 2.2 - Suppose A, B, and X are n n matrices with A, X,...Ch. 2.2 - Explain why the columns of an n n; matrix A are...Ch. 2.2 - Explain why the columns of an n n matrix A span n...Ch. 2.2 - Suppose A is n n and the equation Ax = b has a...Ch. 2.2 - Exercises 25 and 26 prove Theorem 4 for A =...Ch. 2.2 - Exercises 25 and 26 prove Theorem 4 for A =...Ch. 2.2 - Exercises 27 and 28 prove special cases of the...Ch. 2.2 - Show that if row 3 of A is replaced by row3(A) 4 ...Ch. 2.2 - Find the inverses of the matrices in Exercises...Ch. 2.2 - Find die inverses of the matrices in Exercises...Ch. 2.2 - Find die inverses of the matrices in Exercises...Ch. 2.2 - Find die inverses of the matrices in Exercises...Ch. 2.2 - Use the algorithm from this section to find the...Ch. 2.2 - Let A = [279256134]. Find the third column of A1...Ch. 2.2 - [M] Let A = [2592754618053715450149]. Find the...Ch. 2.2 - Let A = [121315]. Constuct a 2 3 matrix C (by...Ch. 2.2 - Let A = [11100111]. Construct a 4 2 matrix D...Ch. 2.2 - Let D = [.005.002.001.002.004.002.001.002.005] be...Ch. 2.3 - Determine if A = [234234234] is invertible.Ch. 2.3 - Suppose that for a certain n n matrix A,...Ch. 2.3 - Suppose that A and B are n n matrices and the...Ch. 2.3 - Unless otherwise specified, assume that all...Ch. 2.3 - Unless otherwise specified, assume that all...Ch. 2.3 - Unless otherwise specified, assume that all...Ch. 2.3 - Unless otherwise specified, assume that all...Ch. 2.3 - Unless otherwise specified, assume that all...Ch. 2.3 - Unless otherwise specified, assume that all...Ch. 2.3 - Unless otherwise specified, assume that all...Ch. 2.3 - Unless otherwise specified, assume that all...Ch. 2.3 - Unless otherwise specified, assume that all...Ch. 2.3 - Unless otherwise specified, assume that all...Ch. 2.3 - An m n upper triangular matrix is one whose...Ch. 2.3 - An m n lower triangular matrix is one whose...Ch. 2.3 - Can a square matrix with two identical columns be...Ch. 2.3 - Is it possible for a 5 5 matrix to be invertible...Ch. 2.3 - If A is invertible, then the columns of A1 are...Ch. 2.3 - If C is 6 6 and the equation Cx = v is consistent...Ch. 2.3 - If the columns of a 7 7 matrix D are linearly...Ch. 2.3 - If n n matrices E and F have the property that EF...Ch. 2.3 - If the equation Gx = y has more than one solution...Ch. 2.3 - If the equation Hx = c is inconsistent for some c...Ch. 2.3 - If an n n matrix K cannot be row reduced to In....Ch. 2.3 - If L is n n and the equation Lx = 0 has the...Ch. 2.3 - Verify the boxed statement preceding Example 1.Ch. 2.3 - Explain why the columns of A2 span n whenever the...Ch. 2.3 - Show that if AB is invertible, so is A. You cannot...Ch. 2.3 - Show that if AB is invertible, so is B.Ch. 2.3 - If A is an n n matrix and the equation Ax = b has...Ch. 2.3 - If A is an n n matrix and the transformation x ...Ch. 2.3 - Suppose A is an n n matrix with the property that...Ch. 2.3 - Suppose A is an n n matrix with the property that...Ch. 2.3 - In Exercises 33 and 34, T is a linear...Ch. 2.3 - In Exercises 33 and 34, T is a linear...Ch. 2.3 - Let T : n n be an invertible linear...Ch. 2.3 - Let T be a linear transformation that maps n onto...Ch. 2.3 - Suppose T and U are linear transformations from n...Ch. 2.3 - Suppose a linear transformation T : n n has the...Ch. 2.3 - Let T : n n be an invertible linear...Ch. 2.3 - Suppose T and S satisfy the invertibility...Ch. 2.4 - Show that[I0AI] is invertible and find its...Ch. 2.4 - Compute XTX, where X is partitioned as [X1 X2].Ch. 2.4 - In Exercises 19, assume that the matrices are...Ch. 2.4 - In Exercises 19, assume that the matrices are...Ch. 2.4 - In Exercises 19, assume that the matrices are...Ch. 2.4 - In Exercises 19, assume that the matrices are...Ch. 2.4 - In Exercises 58, find formulas for X, Y, and Z in...Ch. 2.4 - In Exercises 58, find formulas for X, Y, and Z in...Ch. 2.4 - In Exercises 58, find formulas for X, Y, and Z in...Ch. 2.4 - In Exercises 58, find formulas for X, Y, and Z in...Ch. 2.4 - Suppose A11 is an invertible matrix. Find matrices...Ch. 2.4 - The inverse of [I00CI0ABI] is [I00ZI0XYI]. Find X,...Ch. 2.4 - Let A=[B00C], where B and C are square. Show A is...Ch. 2.4 - Show that the block upper triangular matrix A in...Ch. 2.4 - Suppose A11 is invertible. Find X and Y such that...Ch. 2.4 - Suppose the block matrix A on the left side of (7)...Ch. 2.4 - When a deep space probe is launched, corrections...Ch. 2.4 - a. Verify that A2 = I when A=[1031]. b. Use...Ch. 2.4 - Use partitioned matrices to prove by induction...Ch. 2.4 - Without using row reduction, find the inverse of...Ch. 2.5 - Find an LU factorization of...Ch. 2.5 - In Exercises 16, solve the equation Ax = b by...Ch. 2.5 - In Exercises 16, solve the equation Ax = b by...Ch. 2.5 - In Exercises 16, solve the equation Ax = b by...Ch. 2.5 - In Exercises 16, solve the equation Ax = b by...Ch. 2.5 - In Exercises 16, solve the equation Ax = b by...Ch. 2.5 - In Exercises 16, solve the equation Ax = b by...Ch. 2.5 - Find an LU factorization of the matrices in...Ch. 2.5 - Find an LU factorization of the matrices in...Ch. 2.5 - Find an LU factorization of the matrices in...Ch. 2.5 - Find an LU factorization of the matrices in...Ch. 2.5 - Find an LU factorization of the matrices in...Ch. 2.5 - Find an LU factorization of the matrices in...Ch. 2.5 - Find an LU factorization of the matrices in...Ch. 2.5 - Find an LU factorization of the matrices in...Ch. 2.5 - Find an LU factorization of the matrices in...Ch. 2.5 - Find an LU factorization of the matrices in...Ch. 2.5 - When A is invertible, MATLAB finds A1 by factoring...Ch. 2.5 - Find A1 as in Exercise 17, using A from Exercise...Ch. 2.5 - Let A be a lower triangular n n matrix with...Ch. 2.5 - Let A = LU be an LU factorization. Explain why A...Ch. 2.5 - Suppose A = BC, where B is invertible. Show that...Ch. 2.5 - (Reduced LU Factorization) With A as in the...Ch. 2.5 - (Rank Factorization) Suppose an m n matrix A...Ch. 2.5 - (QR Factorization) Suppose A = QR, where Q and R...Ch. 2.5 - (Singular Value Decomposition) Suppose A = UDVT,...Ch. 2.5 - (Spectral Factorization) Suppose a 3 3 matrix A...Ch. 2.5 - Design two different ladder networks that each...Ch. 2.5 - Show that if three shunt circuits (with...Ch. 2.5 - Prob. 29ECh. 2.5 - Find a different factorization of the A in...Ch. 2.6 - Suppose an economy has two sectors: goods and...Ch. 2.6 - Exercises 14 refer to an economy that is divided...Ch. 2.6 - Exercises 14 refer to an economy that is divided...Ch. 2.6 - Exercises 14 refer to an economy that is divided...Ch. 2.6 - Exercises 14 refer to an economy that is divided...Ch. 2.6 - Consider the production model x = Cx + d for an...Ch. 2.6 - Repeat Exercise 5 with C=[.1.6.5.2], and d=[1811]....Ch. 2.6 - Let C and d be as in Exercise 5. a. Determine the...Ch. 2.6 - Let C be an n n consumption matrix whose column...Ch. 2.6 - Solve the Leontief production equation for an...Ch. 2.6 - The consumption matrix C for the U.S. economy in...Ch. 2.6 - The Leontief production equation, x = Cx + d, is...Ch. 2.6 - Let C be a consumption matrix such that Cm 0 as m...Ch. 2.7 - Rotation of a figure about a point p in 2 is...Ch. 2.7 - What 3 3 matrix will have the same effect on...Ch. 2.7 - Use matrix multiplication to find the image of the...Ch. 2.7 - In Exercises 38, find the 3 3 matrices that...Ch. 2.7 - In Exercises 38, find the 3 3 matrices that...Ch. 2.7 - In Exercises 38, find the 3 3 matrices that...Ch. 2.7 - In Exercises 38, find the 3 3 matrices that...Ch. 2.7 - In Exercises 38, find the 3 3 matrices that...Ch. 2.7 - In Exercises 38, find the 3 3 matrices that...Ch. 2.7 - A 2 200 data matrix D contains the coordinates of...Ch. 2.7 - Consider the following geometric 2D...Ch. 2.7 - Prob. 11ECh. 2.7 - A rotation in 2 usually requires four...Ch. 2.7 - The usual transformations on homogeneous...Ch. 2.7 - Prob. 14ECh. 2.7 - What vector in 3 has homogeneous coordinates...Ch. 2.7 - Are (1. 2, 3, 4) and (10, 20, 30, 40) homogeneous...Ch. 2.7 - Give the 4 4 matrix that rotates points in 3...Ch. 2.7 - Give the 4 4 matrix that rotates points in 3...Ch. 2.7 - Let S be the triangle with vertices (4.2, 1.2,4),...Ch. 2.7 - Let S be the triangle with vertices (9,3,5),...Ch. 2.7 - [M] The actual color a viewer sees on a screen is...Ch. 2.7 - [M] The signal broadcast by commercial television...Ch. 2.8 - Let A=[115207353] and u=[732] Is u in Nul A? Is u...Ch. 2.8 - Given A=[010001000], find a vector in Nul A and a...Ch. 2.8 - Suppose an n n matrix A is invertible. What can...Ch. 2.8 - Exercises 14 display sets in 2. Assume the sets...Ch. 2.8 - Exercises 14 display sets in 2. Assume the sets...Ch. 2.8 - Exercises 14 display sets in 2. Assume the sets...Ch. 2.8 - Exercises 1-4 display sets in 2. Assume the sets...Ch. 2.8 - Let v1 = [235], v2 = [458], and w = [829]....Ch. 2.8 - Let v1 = [1243], v2 = [4797], v3 = [5865], and u =...Ch. 2.8 - Let v1 = [286], v2 = [387], v3 = [467], p =...Ch. 2.8 - Let v1 = [306], v2 = [223], v3 = [063], and p =...Ch. 2.8 - With A and p as in Exercise 7, determine if p is...Ch. 2.8 - With u = (2, 3, 1) and A as in Exercise 8,...Ch. 2.8 - In Exercises 11 and 12. give integers p and q such...Ch. 2.8 - In Exercises 11 and 12. give integers p and q such...Ch. 2.8 - For A as in Exercise 11, find a nonzero vector in...Ch. 2.8 - For A as in Exercise 12, find a nonzero vector in...Ch. 2.8 - Determine which sets in Exercises 15-20 are bases...Ch. 2.8 - Determine which sets in Exercises 15-20 are bases...Ch. 2.8 - Determine which sets in Exercises 15-20 are bases...Ch. 2.8 - Determine which sets in Exercises 15-20 are bases...Ch. 2.8 - Determine which sets in Exercises 15-20 are bases...Ch. 2.8 - Determine which sets in Exercises 15-20 are bases...Ch. 2.8 - Exercises 23-26 display a matrix A and an echelon...Ch. 2.8 - Exercises 23-26 display a matrix A and an echelon...Ch. 2.8 - Exercises 23-26 display a matrix A and an echelon...Ch. 2.8 - Exercises 23-26 display a matrix A and an echelon...Ch. 2.8 - Construct a nonzero 3 3 matrix A and a nonzero...Ch. 2.8 - Construct a nonzero 3 3 matrix A and a vector b...Ch. 2.8 - Construct a nonzero 3 3 matrix A and a nonzero...Ch. 2.8 - Suppose the columns of a matrix A = [a1 ap] are...Ch. 2.8 - In Exercises 31-36, respond as comprehensively as...Ch. 2.8 - In Exercises 31-36. respond as comprehensively as...Ch. 2.8 - In Exercises 31-36, respond as comprehensively as...Ch. 2.8 - In Exercises 31-36, respond as comprehensively as...Ch. 2.8 - In Exercises 31-36, respond as comprehensively as...Ch. 2.8 - In Exercises 31-36, respond as comprehensively as...Ch. 2.8 - [M] In Exercises 37 and 38, construct bases for...Ch. 2.8 - [M] In Exercises 37 and 38, construct bases for...Ch. 2.9 - Determine the dimension of the subspace H of 3...Ch. 2.9 - Prob. 2PPCh. 2.9 - Could 3 possibly contain a four-dimensional...Ch. 2.9 - In Exercises 1 and 2, find the vector x determined...Ch. 2.9 - In Exercises 1 and 2, find the vector x determined...Ch. 2.9 - In Exercises 3-6, the vector s is in a subspace H...Ch. 2.9 - In Exercises 1 and 2, find the vector x determined...Ch. 2.9 - In Exercises 3-6, the vector x is in a subspace H...Ch. 2.9 - In Exercises 3-6, the vector x is in a subspace H...Ch. 2.9 - Let b1 = [30], b2 = [12], w = [72], x = [41], and...Ch. 2.9 - Let b1 = [02], b2 = [21], x = [23], y = [24], z =...Ch. 2.9 - Exercises 9-12 display a matrix A and an echelon...Ch. 2.9 - Exercises 9-12 display a matrix A and an echelon...Ch. 2.9 - Exercises 9-12 display a matrix A and an echelon...Ch. 2.9 - Exercises 9-12 display a matrix A and an echelon...Ch. 2.9 - In Exercises 13 and 14, find a basis for the...Ch. 2.9 - In Exercises 13 and 14, find a basis for the...Ch. 2.9 - Suppose a 3 5 matrix A has three pivot columns....Ch. 2.9 - Suppose a 4 7 matrix A has three pivot columns....Ch. 2.9 - If the subspace of all solutions of Ax = 0 has a...Ch. 2.9 - What is the rank of a 4 5 matrix whose null space...Ch. 2.9 - If the tank of a 7 6 matrix A is 4, what is the...Ch. 2.9 - Show that a set of vectors {v1, v2, , v5} in n is...Ch. 2.9 - If possible, construct a 3 4 matrix A such that...Ch. 2.9 - Constructa4 3 matrix with tank 1.Ch. 2.9 - Let A be an n p matrix whose column space is...Ch. 2.9 - Suppose columns 1, 3, 5, and 6 of a matrix A are...Ch. 2.9 - Suppose vectors b1, bp span a subspace W, and let...Ch. 2.9 - Prob. 37ECh. 2.9 - [M] Let H = Span {v1, v2, v3} and B= {v1, v2,...Ch. 2 - Find the matrix C whose inverse is C1 = [4567].Ch. 2 - Show that A = [000100010]. Show that A3 = 0. Use...Ch. 2 - Suppose An = 0 for some n 1. Find an inverse for...Ch. 2 - Suppose an n n matrix A satisfies the equation A2...Ch. 2 - Prob. 20SECh. 2 - Let A = [1382411125] and B = [351534]. Compute A1B...Ch. 2 - Find a matrix A such that the transformation x Ax...Ch. 2 - Suppose AB =[5423] and B = [7321]. Find A.Ch. 2 - Suppose A is invertible. Explain why ATA is also...Ch. 2 - Let x1, , xn, be fixed numbers. The matrix below,...Ch. 2 - Prob. 26SECh. 2 - Given u in n with uTu = 1, Let P = uuT (an outer...Ch. 2 - Prob. 28SECh. 2 - Prob. 29SECh. 2 - Let A be an n n singular matrix Describe how to...Ch. 2 - Let A be a 6 4 matrix and B a 4 6 matrix. Show...Ch. 2 - Suppose A is a 5 3 matrix and mere exists a 3 5...Ch. 2 - Prob. 33SECh. 2 - [M] Let An be the n n matrix with 0s on the main...
Additional Math Textbook Solutions
Find more solutions based on key concepts
True or False The quotient of two polynomial expressions is a rational expression, (p. A35)
Precalculus
Reading, Writing, and Rounding Whole Numbers Write in words. 357
Mathematics for the Trades: A Guided Approach (11th Edition) (What's New in Trade Math)
Provide an example of a qualitative variable and an example of a quantitative variable.
Elementary Statistics ( 3rd International Edition ) Isbn:9781260092561
In Exercises 5-36, express all probabilities as fractions.
23. Combination Lock The typical combination lock us...
Elementary Statistics
The largest polynomial that divides evenly into a list of polynomials is called the _______.
Elementary & Intermediate Algebra
23. A plant nursery sells two sizes of oak trees to landscapers. Large trees cost the nursery $120 from the gro...
College Algebra (Collegiate Math)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Solve questions by Course Name Ordinary Differential Equationsarrow_forwardDetermine whether it's true or false and the reasoning is neededarrow_forward1. (20 pts) Determine whether the following statements are true (T) or false (F)? (A reasoning is required.) (1) Let V be the set of all ordered pairs of real numbers. Consider the following addition and scalar multiplication operations on u = u= (u1, u2) and v = (v1, v2): u + v = (U₁ + V₁, U₂ + v₂), ku = (ku₁, u₂). Is V a vector space under the above operations? U2 (2) The set Mmxn of all m×n matrices with the usual operations of addition and scalar multiplication is a vector space. α (3) The dimension of the vector space of all matrices A = [a b] in R2×2 with a+d=0 is 4. (4) The coordinate vector of p(x) = 2-x+x² in P3 relative to the basis S = {1, 1+x, x + x2} is [4 -2 1]. (5) If a 6×4 matrix A has a rank 3, then the dimension of N(A) is 3.arrow_forward
- 5. (20%) The linear transformation L: P3 → P2 defined by L(f(x)) = f'(x)+ f(0). (a) Find the representing matrix A of L with respect to the ordered basis {x2, x, 1} for P3, and the ordered basis {2,1 - x} for P2. (b) Find the coordinates of the f(x) = 2x² +2 in P3 with respect to the ordered basis {x2,-x, 1}, and find the coordinates of L(f(x)) with respect to the ordered basis {2,1-x}arrow_forwardFor the spinner below, assume that the pointer can never lie on a borderline. Find the following probabilities. (enter the probabilities as fractions)arrow_forwardQuestions 1. Identify and describe potential bias in the study. 2. Identify and describe the way in which the selected participants may or may not represent the population as a whole. 3. Identify and describe the possible problems with the end results since the majority will be from females rather than an even split. 4. Identify and describe the possible problems with identifying females as possibly more vulnerable based on the data collected. 5. Identify a possible null hypothesis and problems in how the study might address this null hypothesis. 6. Identify one possible method of improving the study design and describe how it would improve the validity of the conclusions. 7. Identify a second possible method of improving the study design and describe how it would improve the validity of the conclusions.arrow_forward
- The Course Name Real Analysis please Solve questions by Real Analysisarrow_forwardpart 3 of the question is: A power outage occurs 6 min after the ride started. Passengers must wait for their cage to be manually cranked into the lowest position in order to exit the ride. Sine function model: where h is the height of the last passenger above the ground measured in feet and t is the time of operation of the ride in minutes. What is the height of the last passenger at the moment of the power outage? Verify your answer by evaluating the sine function model. Will the last passenger to board the ride need to wait in order to exit the ride? Explain.arrow_forward2. The duration of the ride is 15 min. (a) How many times does the last passenger who boarded the ride make a complete loop on the Ferris wheel? (b) What is the position of that passenger when the ride ends?arrow_forward
- 3. A scientist recorded the movement of a pendulum for 10 s. The scientist began recording when the pendulum was at its resting position. The pendulum then moved right (positive displacement) and left (negative displacement) several times. The pendulum took 4 s to swing to the right and the left and then return to its resting position. The pendulum's furthest distance to either side was 6 in. Graph the function that represents the pendulum's displacement as a function of time. Answer: f(t) (a) Write an equation to represent the displacement of the pendulum as a function of time. (b) Graph the function. 10 9 8 7 6 5 4 3 2 1 0 t 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 -1 -5. -6 -7 -8 -9 -10-arrow_forwardA power outage occurs 6 min after the ride started. Passengers must wait for their cage to be manually cranked into the lowest position in order to exit the ride. Sine function model: h = −82.5 cos (3πt) + 97.5 where h is the height of the last passenger above the ground measured in feet and t is the time of operation of the ride in minutes. (a) What is the height of the last passenger at the moment of the power outage? Verify your answer by evaluating the sine function model. (b) Will the last passenger to board the ride need to wait in order to exit the ride? Explain.arrow_forwardThe Colossus Ferris wheel debuted at the 1984 New Orleans World's Fair. The ride is 180 ft tall, and passengers board the ride at an initial height of 15 ft above the ground. The height above ground, h, of a passenger on the ride is a periodic function of time, t. The graph displays the height above ground of the last passenger to board over the course of the 15 min ride. Height of Passenger in Ferris Wheel 180 160 140- €120 Height, h (ft) 100 80 60 40 20 0 ך 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Time of operation, t (min) Sine function model: h = −82.5 cos (3πt) + 97.5 where h is the height of the passenger above the ground measured in feet and t is the time of operation of the ride in minutes. What is the period of the sine function model? Interpret the period you found in the context of the operation of the Ferris wheel. Answer:arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Vector Spaces | Definition & Examples; Author: Dr. Trefor Bazett;https://www.youtube.com/watch?v=72GtkP6nP_A;License: Standard YouTube License, CC-BY
Understanding Vector Spaces; Author: Professor Dave Explains;https://www.youtube.com/watch?v=EP2ghkO0lSk;License: Standard YouTube License, CC-BY