To find the LU decomposition of Matrix A given as:
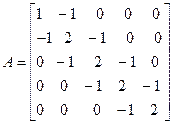
Explanation of Solution
LU Decomposition of A: The LU Decomposition of A means to decompose a matrix A into a product of lower triangular matrix and upper triangular matrix.
In Decomposition of A the input is lower triangular matrix and output is upper triangular matrix obtain by applying following row operation on A.
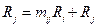
Here,
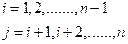
and
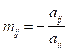
And lower triangular matrix is given by
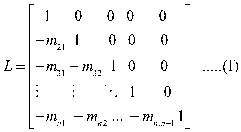
Consider a matrix,
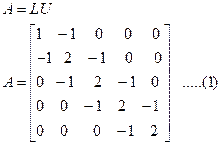
Initially calculate the value of all entries other than 0 and 1 of equation (1).
Apply the row operation to the matrix A to find the upper triangular matrix U
Calculate the value of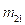 
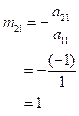(2)
Calculate the value of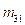 
,
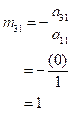(3)
Calculate the value of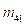 
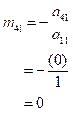(4)
Calculate the value of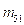 
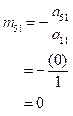(5)
Apply row transformation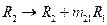 
to find upper triangular matrix.
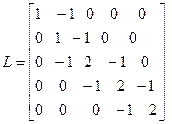
Similarly calculate the value of,
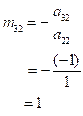…… (6)
Calculate the value of,
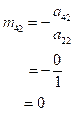…… (7)
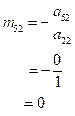…… (8)
Apply row transformation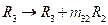 
to find upper triangular matrix.
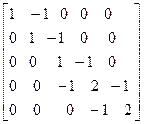
Calculate the value of,
(9)
Calculate the value of,
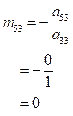(10)
Apply row transformation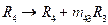 
to find upper triangular matrix.
The upper triangular matrix is-
The lower triangular matrix is-
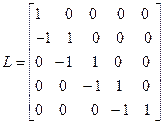
Hence, the LU decomposition of A is-
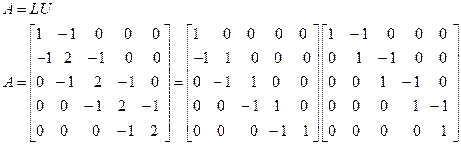
To solve the equation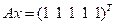 
by using forward and backward substitution.
Explanation of Solution
Consider an expression-
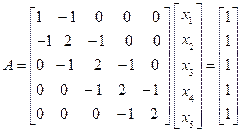
To solve this, the following steps are followed-
Express 
in the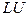 
decomposition form-
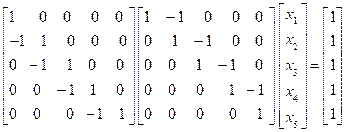
Let for any
• LUP Decomposition
• Forward Substitution
Let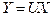 
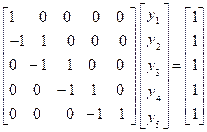
After solving, the following value of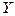 
is obtained-
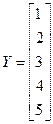
• Backward Substitution
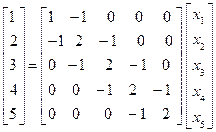
Solving for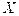 
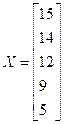
To find the inverse of A.
Explanation of Solution
Inverse of a matrix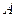 
is a matrix 
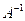such that 
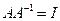where 
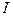is an identity matrix.
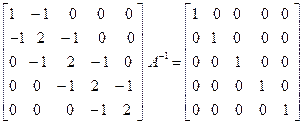
To solve this, the following steps are followed-
• Forward Substitution
Let 
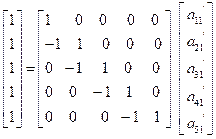
After solving, the following value of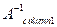 
is obtained-
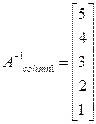
Similarly, other columns can also be obtained in the following way-
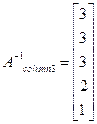
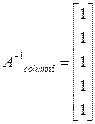
Inverse of the matrix can be formed by using the five results which comprises the columns of the inverse matrix.
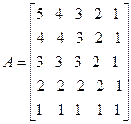
• Backward Substitution
Now find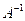 
from 
Solving for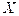 
To show how, for any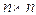 
symmetric positive-definite, tridiagonal matrix 
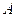and any n-vector 
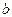to solve the equation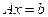
Explanation of Solution
Inverse of a matrix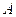 
is a matrix 
such that 
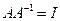where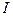 
is an identity matrix.
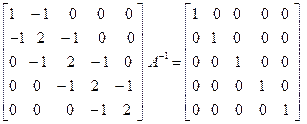
To solve this, the following steps are followed-
• Forward Substitution
Let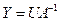 
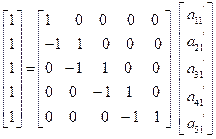
After solving, the following value of 
is obtained-
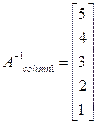
Similarly, other columns can also be obtained in the following way-
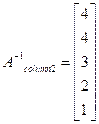
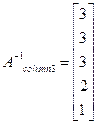
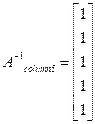
Inverse of the matrix can be formed by using the five results which comprises the columns of the inverse matrix.
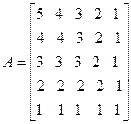
• Backward Substitution
Now find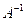 
from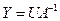 
Solving for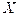 
To show that, for any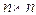 
non-singular, tridiagonal matrix.
Explanation of Solution
Forward and Backward substitution take the same amount of operations as in the previous case. The only different case is the decomposition step. In this case, the decomposition is done into unit lower triangular and upper triangular matrix, and. The pivoting is done by the swapping rows such that the highest element of a column comes to the diagonal place. The decomposition looks like the following:
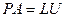
Here,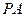 
loses the tri-diagonal property of matrix
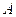but it is still a banded matrix. The essence to solve this is similar to the tri-diagonal case. The time complexity now depends on the width of the band or the distance between the farthest diagonals of the resultant matrix. Matrix becomes wider than the upper triangle of the initial matrix. The final complexity becomes
Hence the time complexity of LUP decomposition 
Want to see more full solutions like this?
- map the following ER diagram into a relational database schema diagram. you should take into account all the constraints in the ER diagram. Underline the primary key of each relation, and show each foreign key as a directed arrow from the referencing attributes (s) to the referenced relation. NOTE: Need relational database schema diagramarrow_forwardWhat is business intelligence? Share the Business intelligence (BI) tools you have used and explain what types of decisions you made.arrow_forwardI need help fixing the minor issue where the text isn't in the proper place, and to ensure that the frequency cutoff is at the right place. My code: % Define frequency range for the plot f = logspace(1, 5, 500); % Frequency range from 10 Hz to 100 kHz w = 2 * pi * f; % Angular frequency % Parameters for the filters - let's adjust these to get more reasonable cutoffs R = 1e3; % Resistance in ohms (1 kΩ) C = 1e-6; % Capacitance in farads (1 μF) % For bandpass, we need appropriate L value for desired cutoffs L = 0.1; % Inductance in henries - adjusted for better bandpass response % Calculate cutoff frequencies first to verify they're in desired range f_cutoff_RC = 1 / (2 * pi * R * C); f_resonance = 1 / (2 * pi * sqrt(L * C)); Q_factor = (1/R) * sqrt(L/C); f_lower_cutoff = f_resonance / (sqrt(1 + 1/(4*Q_factor^2)) + 1/(2*Q_factor)); f_upper_cutoff = f_resonance / (sqrt(1 + 1/(4*Q_factor^2)) - 1/(2*Q_factor)); % Transfer functions % Low-pass filter (RC) H_low = 1 ./ (1 + 1i * w *…arrow_forward
- Task 3. i) Compare your results from Tasks 1 and 2. j) Repeat Tasks 1 and 2 for 500 and 5,000 elements. k) Summarize run-time results in the following table: Time/size n String StringBuilder 50 500 5,000arrow_forwardCan you please solve this without AIarrow_forward1. Create a Vehicle.java file. Implement the public Vehicle and Car classes in Vehicle.java, including all the variables and methods in the UMLS. Vehicle - make: String model: String -year: int + Vehicle(String make, String, model, int, year) + getMake(): String + setMake(String make): void + getModel(): String + setModel(String model): void + getYear(): int + set Year(int year): void +toString(): String Car - numDoors: int + numberOfCar: int + Car(String make, String, model, int, year, int numDoors) + getNumDoors(): int + setNumDoors (int num Doors): void + toString(): String 2. Create a CarTest.java file. Implement a public CarTest class with a main method. In the main method, create one Car object and print the object using System.out.println(). Then, print the numberOfCar. Your printing result must follow the example output: make Toyota, model=Camry, year=2022 numDoors=4 1 Hint: You need to modify the toString methods in the Car class and Vehicle class!arrow_forward
- CHATGPT GAVE ME WRONG ANSWER PLEASE HELParrow_forwardHELP CHAT GPT GAVE ME WRONG ANSWER Consider the following implementation of a container that will be used in a concurrent environment. The container is supposed to be used like an indexed array, but provide thread-safe access to elements. struct concurrent_container { // Assume it’s called for any new instance soon before it’s ever used void concurrent_container() { init_mutex(&lock); } ~concurrent_container() { destroy_mutex(&lock); } // Returns element by its index. int get(int index) { lock.acquire(); if (index < 0 || index >= size) { return -1; } int result = data[index]; lock.release(); return result; } // Sets element by its index. void set(int index, int value) { lock.acquire(); if (index < 0 || index >= size) { resize(size); } data[index] = value; lock.release(); } // Extend maximum capacity of the…arrow_forwardWrite a C program using embedded assembler in which you use your own function to multiply by two without using the product. Tip: Just remember that multiplying by two in binary means shifting the number one place to the left. You can use the sample program from the previous exercise as a basis, which increments a variable. Just replace the INC instruction with SHL.arrow_forward
Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole
C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr