
Concept explainers
A particle in the cyclotron shown in Figure 28.16a gains energy qΔV from the alternating power supply each time it passes from one dee to the other. The time interval for each full orbit is
so the particle’s average rate of increase in energy’ is
Notice that this power input is constant in time. On the other hand, the rate of increase in the radius r of its path is not constant. (a) Show that the rate of increase in the radius r of the panicle’s path is given by
(b) Describe how the path of the particles in Figure 28.16a is consistent with the result of part (a). (c) At what rate is the radial position of the protons in a cyclotron increasing immediately before the protons leave the cyclotron? Assume the cyclotron has an outer radius of 0.350 m, an accelerating voltage of ΔV = 600 V, and a magnetic field of magnitude 0.800 T. (d) By how much does the radius of the protons’ path increase during their last full revolution?
Figure 28.16 (a) A cyclotron consists of an ion source at P, two does D1 and D2 across which an alternating potential difference is applied, and a uniform magnetic field. (The south pole of the magnet is not shown.) (b) The first cyclotron, invented by E. O. Lawrence and M. S. Livingston in 1934.
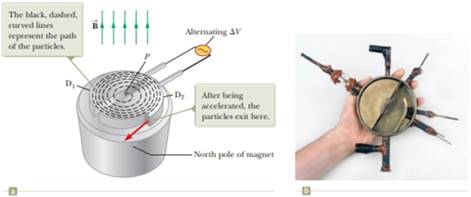
(a)
To prove: The rate of increase in the radius
Answer to Problem 18P
Explanation of Solution
Given Info: The time interval of full orbit is
The formula for the energy is,
Here,
Differentiating equation (1) with respect to time
The above equation can be rewritten as,
Substitute
The formula for the centripetal force is,
The above equation can be rewritten as,
Differentiating equation (3) with respect to time
Deducing from equation (2) and equation (4),
Conclusion:
Therefore, the rate of increase in the radius
(b)
Answer to Problem 18P
Explanation of Solution
Given Info: The time interval of full orbit is
The formula of change of radius with time is,
The value of the path of the particle is consistent with respect to time as according to the above formula the path is dependent on the radius of circle and the magnitude of the magnetic field which remains constant for a path.
Thus, the path of the particle is consistent.
Conclusion:
Therefore, the path of the particle is consistent.
(c)
Answer to Problem 18P
Explanation of Solution
Given Info: The time interval of full orbit is
The formula for the change of radius with time is,
Substitute
Thus, the rate of increase of the radial direction of proton is
Conclusion:
Therefore, the rate of increase of the radial direction of proton is
(d)
Answer to Problem 18P
Explanation of Solution
Given Info: The time interval of full orbit is
The formula for the velocity is,
Substitute
Thus, the velocity of proton is
The formula for the energy is,
Substitute
The formula for the energy at the end is,
Substitute
The formula for the radius at the end is,
Substitute
The formula for the increase in the radius is,
Substitute
Thus the increase in the radius of the path of proton is
Conclusion:
Therefore, increase in the radius of the path of proton is
Want to see more full solutions like this?
Chapter 28 Solutions
PHYSICS:F/SCI.+ENGRS-W/WEBASSIGN
- I need help with how to solve this answer, thank you !arrow_forwardIs work function of a metals surface related to surface energy and surface tension? What is the need to the work function component in the math of tension of metal surfaces that cannot be provided by existing equations of surface energy and surface tension? What are the key differences in each parameter and variables that allow for a differentiation of each function? What has a more significant meaning work function, surface tension or surface energy? Are there real differences and meaning? Please clarify and if possible provide examples . Does surface tension dependant on thickness of a metal or type of metal surface all having the same thickness? Clearly temperature has a profound change on surface tension what other variables besides temperature are key to surface tension. What if any is there a connection between crystal structure of the element and surface energy and tension? This is NOT a Assignment Question!!!arrow_forwardThe cylindrical beam of a 12.7-mW laser is 0.920 cm in diameter. What is the rms value of the electric field? V/marrow_forward
- Consider a rubber rod that has been rubbed with fur to give the rod a net negative charge, and a glass rod that has been rubbed with silk to give it a net positive charge. After being charged by contact by the fur and silk...? a. Both rods have less mass b. the rubber rod has more mass and the glass rod has less mass c. both rods have more mass d. the masses of both rods are unchanged e. the rubber rod has less mass and the glass rod has mroe massarrow_forward8) 9)arrow_forward10) 11) 12) 13) 14) 15)arrow_forward

 Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning
Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning





