Chapter 28, Problem 18P

Perform the same computation for the Lorenz equations in Sec. 28.2, but use (a) Euler's method, (b) Heun's method (without iterating the corrector), (c) the fourth-order RK method, and (d) the MATLAB ode45 function. In all cases use single-precision variables and a step size of 0.1 and simulate from $t=0$ to 20. Develop phase-plane plots for all cases.

To determine

To calculate: The solution of Lorentz equation $\frac{dx}{dt}=-10x+10y,\frac{dy}{dt}=28x-y-xz$ and $\frac{dz}{dt}=-2.666667z+xy$ by the Euler’s method with the step size of 0.1 from $t=0\text{ to }20$. Also plot the result and the phase-plane plot.

Answer to Problem 18P

Solution:

The solution of Lorentz equations by the Euler’s method with step size 0.1 gives unstable solution.

Explanation of Solution

Given Information:

Lorentz equations,

$\begin{array}{c}\frac{dx}{dt}=-10x+10y\\ \frac{dy}{dt}=28x-y-xz\\ \frac{dz}{dt}=-2.666667z+xy\end{array}$

and Initial conditions are $x=y=z=5$.

Formula used:

Euler’s method for $\frac{dy}{dx}=f\left(x,y\right)$ is,

$y\left(x+h\right)=y\left(x\right)+hf\left(x,y\right)$

Where, h is the step size.

Calculation:

Consider the equations,

$\begin{array}{c}\frac{dx}{dt}=-10x+10y\\ \frac{dy}{dt}=28x-y-xz\\ \frac{dz}{dt}=-2.666667z+xy\end{array}$

The iteration formula for Euler’s method with step size $\Delta t=0.1$ for the above equations are,

$\begin{array}{c}x\left(t+0.1\right)=x\left(t\right)+0.1\left(-10x+10y\right)\\ y\left(t+0.1\right)=y\left(t\right)+0.1\left(28x-y-xz\right)\\ z\left(t+0.1\right)=z\left(t\right)+0.1\left(-2.666667z+xy\right)\end{array}$

Use excel to find all the iteration with step size $\Delta t=0.1$ as below,

Step 1: Name the column A as t and go to column A2 and put 0 then go to column A3 and write the formula as,

=A2+0.1

Then, Press enter and drag the column up to $t=20$.

Step 2: Now name the column B as x-Euler and go to column B2 and write 5 and then go to the column B3 and write the formula as,

=B2+0.1*(-10*B2+10*C2)

Step 3: Press enter and drag the column up to $t=20$.

Step 4: Now name the column C as y-Euler and go to column C2 and write 5 and then go to the column C3 and write the formula as,

=C2+0.1*(28*B2-C2-B2*D2)

Step 5: Press enter and drag the column up to $t=20$.

Step 6: Now name the column D as z-Euler and go to column D2 and write 5 and then go to the column D3 and write the formula as,

=D2+0.1*(-2.666667*D2+B2*C2)

Step 7: Press enter and drag the column up to $t=20$.

Thus, first few iterations are as shown below,

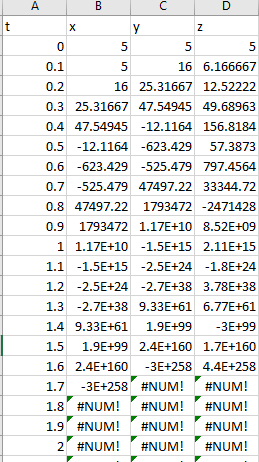
From the above result, it is observed that the solution of Lorentz equations by the Euler’s method with step size 0.1 the values are continuously decreasing. Hence, Euler method with step size 0.1 gives unstable solution for the Lorentz equations.

To determine

To calculate: The solution of Lorentz equation $\frac{dx}{dt}=-10x+10y,\frac{dy}{dt}=28x-y-xz$ and $\frac{dz}{dt}=-2.666667z+xy$ by the Heun’s method with the step size of 0.1 from $t=0\text{ to }20$. Also plot the result and the phase-plane plot.

Answer to Problem 18P

Solution:

The solution of Lorentz equations by the Heun’s method with step size 0.1 gives unstable solution.

Explanation of Solution

Given Information:

Lorentz equations,

$\begin{array}{c}\frac{dx}{dt}=-10x+10y\\ \frac{dy}{dt}=28x-y-xz\\ \frac{dz}{dt}=-2.666667z+xy\end{array}$

and Initial conditions are $x=y=z=5$.

Formula used:

The iteration formula for Heun’s method is,

$y_{i+1}=y_i+\frac{h}{2}\left(f\left(x_i,y_i\right)+f\left(x_i+h,y_i+hf\left(x_i,y_i\right)\right)\right)$

Calculation:

Consider the equations,

$\begin{array}{c}\frac{dx}{dt}=-10x+10y\\ \frac{dy}{dt}=28x-y-xz\\ \frac{dz}{dt}=-2.666667z+xy\end{array}$

The following VBA code is used to solve the Lorentz equation by Heun’s method:

Code:

OptionExplicit

'Generate a function find

Subfind()

'Declare the variables

Dim t AsDouble,x AsDouble,h AsDouble,hhAsDouble,y AsDouble,z AsDouble,g AsDouble,r AsDouble

'Set the values for variables

t =0

x =5

h =0.1

y =5

z =5

g =28

r =28

'move to the cell b3

Range("b3").Select

ActiveCell. Value="Heun Method"

'Assign name to the columns

ActiveCell. Offset(1, 0).Select

ActiveCell. Value="t"

ActiveCell. Offset(0, 1).Select

ActiveCell. Value="x"

ActiveCell. Offset(0, 1).Select

ActiveCell. Value="y"

ActiveCell. Offset(0, 1).Select

ActiveCell. Value="z"

'call the Heun function

hh=Heun(t,x,h,y,z)

EndSub

'Define Heun function

FunctionHeun(t,x,h,y,z)

'Declare the variables

Dim dx1dt AsDouble,slpxAsDouble,dx2dt AsDouble,cexAsDouble,xnewAsDouble,dz2dt AsDouble,znewAsDouble

Dim dy1dt AsDouble,dz1dt AsDouble,slpyAsDouble,dy2dt AsDouble,ceyAsDouble,ynewAsDouble,slpzAsDouble,cezAsDouble

Dim j AsInteger

'Use for loop to find the different value of x

For j =1To200

'move to cell b4

Range("b4").Select

'Display the values of t, x, y and z

ActiveCell. Offset(j, 0).Select

ActiveCell. Value= t

ActiveCell. Offset(0, 1).Select

ActiveCell. Value= x

ActiveCell. Offset(0, 1).Select

ActiveCell. Value= y

ActiveCell. Offset(0, 1).Select

ActiveCell. Value= z

'call drive function for dx1dt

dx1dt =drivex(t,x)

cex= x +(dx1dt * h)

'call drive function for dx2dt

dx2dt =drivex(t + h,cex)

slpx=(dx1dt + dx2dt)/2

'Write the formula for next value of x

xnew= x +slpx* h

x =xnew

'call drive function for dy1dt

dy1dt =drivey(t,y)

cey= y +(dy1dt * h)

'call drive function for dy2dt

dy2dt =drivey(t + h,cey)

slpy=(dy1dt + dy2dt)/2

'Write the formula for next value of y

ynew= y +slpy* h

y =ynew

'call drive function for dz1dt

dz1dt =drivey(t,z)

cez= z +(dz1dt * h)

'call drive function for dz2dt

dz2dt =drivez(t + h,cez)

slpz=(dz1dt + dz2dt)/2

'Write the formula for next value of z

znew= z +slpz* h

z =znew

'Write the formula for next value of t

t = t + h

Next

EndFunction

'define drivex function

Functiondrivex(t,x)

Dim temp AsDouble

'find the value of derivative

temp =-(28* x)+(28*5)

drivex= temp

EndFunction

'define drivey function

Functiondrivey(t,y)

Dim temp AsDouble

'find the value of derivative

temp =(28*5)+(y)-(5*5)

drivey= temp

EndFunction

'define drivez function

Functiondrivez(t,z)

Dim temp AsDouble

'find the value of derivative

temp =-(5* z)+(5*5)

drivez= temp

EndFunction

Output:

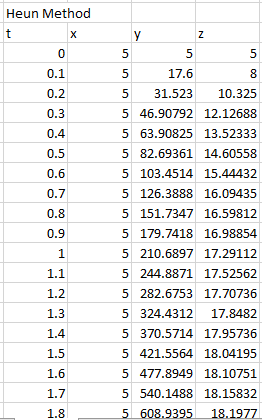
To draw the graph of the above results, follow the steps in excel sheet as given below,

Step 1: Select the cell from A4 to A205 and cell B4 to B205. Then, go to the Insert and select the scatter with smooth lines from the chart.

Step 2: Select the cell from A4 to A205 and cell C4 to C205. Then, go to the Insert and select the scatter with smooth lines from the chart.

Step 2: Select the cell from A4 to A205 and cell D4 to D205. Then, go to the Insert and select the scatter with smooth lines from the chart.

Step 4: Select one of the graphs and paste it on another graph to merge the graphs.

The graph obtained is,

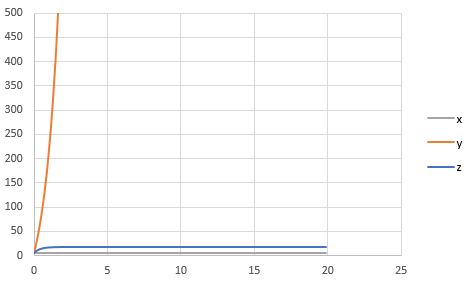
And, to draw the phase plane plot follow the steps as below,

Step 4: Select the column B, column C and column D. Then, go to the Insert and select the scatter with smooth lines from the chart.

The graph obtained is,

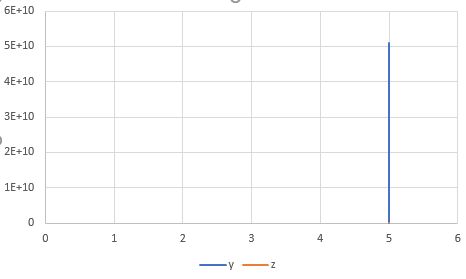
The phase plane plot is a straight line because solution of x is a constant value. The solution o0f Lorentz equation by Heun’s method with step size 0.1 is thus unstable.

To determine

To calculate: The solution of Lorentz equation $\frac{dx}{dt}=-10x+10y,\frac{dy}{dt}=28x-y-xz$ and $\frac{dz}{dt}=-2.666667z+xy$ by the fourth-order RK method with the step size of 0.1 from $t=0\text{ to }20$. Also plot the result and the phase-plane plot.

Answer to Problem 18P

Solution:

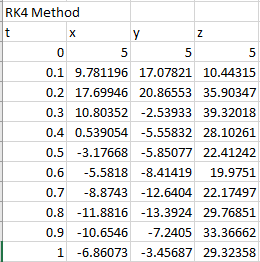
The first few solutions of Lorentz equation are,

t	x	y	z
0	5	5	5
0.1	9.781196	17.07821	10.44315
0.2	17.69946	20.86553	35.90347
0.3	10.80352	-2.53933	39.32018
0.4	0.539054	-5.55832	28.10261
0.5	-3.17668	-5.85077	22.41242
0.6	-5.5818	-8.41419	19.9751
0.7	-8.8743	-12.6404	22.17497
0.8	-11.8816	-13.3924	29.76851
0.9	-10.6546	-7.2405	33.36662
1	-6.86073	-3.45687	29.32358

Explanation of Solution

Given Information:

Lorentz equations,

$\begin{array}{c}\frac{dx}{dt}=-10x+10y\\ \frac{dy}{dt}=28x-y-xz\\ \frac{dz}{dt}=-2.666667z+xy\end{array}$

and Initial conditions are $x=y=z=5$.

Formula used:

The fourth-order RK method for $\frac{dy}{dt}=f\left(t,y\right)$ is,

$\begin{array}{c}{y}_{n+1}=y_n+\frac{1}{6}\left(k_1+2k_2+2k_3+k_4\right)\\ t_{n+1}=t_n+h\end{array}$

Where,

$\begin{array}{c}{k}_1=hf\left(t_n,y_n\right)\\ k_2=hf\left(t_n+\frac{h}{2},y_n+\frac{k_1}{2}\right)\\ k_3=hf\left(t_n+\frac{h}{2},y_n+\frac{k_2}{2}\right)\\ k_4=hf\left(t_n+h,y_n+k_3\right)\end{array}$

Calculation:

The following VBA code is used to find the solution of Lorentz equation by the fourth order RK method:

Code:

OptionExplicit

' Generate a subfunction RK4

Sub RK4()

'Declare the variables as integer

DimiAsInteger,m AsInteger,n AsInteger,j AsInteger

'Declare the variables as double

Dimx_iAsDouble,y_i(10)AsDouble,x_fAsDouble

DimdiffxAsDouble,x_outAsDouble

Dimx_p(200)AsDouble,y_p(200, 10)AsDouble

'Set the values

n =3

x_i=0

x_f=20

y_i(1)=5

y_i(2)=5

y_i(3)=5

diffx=0.1

x_out=0.1

'move to the cell b3

Range("a3").Select

ActiveCell. Value="RK4 Method"

'Assign name to the columns

ActiveCell. Offset(1, 0).Select

ActiveCell. Value="t"

ActiveCell. Offset(0, 1).Select

ActiveCell. Value="x"

ActiveCell. Offset(0, 1).Select

ActiveCell. Value="y"

ActiveCell. Offset(0, 1).Select

ActiveCell. Value="z"

' Call ODESolver to solve the differential equations

CallODESolver(x_i,y_i,x_f,diffx,x_out,x_p,y_p,m,n)

'Display the results

Sheets("Sheet1").Select

Range("a5:n205").ClearContents

Range("a5").Select

'Use for loop to store different values of x_p

Fori=0To m

ActiveCell. Value=x_p(i)

'Use for loop to store different values of y_p

For j =1To n

'Define the offset

ActiveCell. Offset(0, 1).Select

ActiveCell. Value=y_p(i,j)

Next j

'Define the offset

ActiveCell. Offset(1,-n).Select

Nexti

Range("a5").Select

EndSub

' Define subfunction ODESolver

SubODESolver(x_i,y_i,x_f,diffx,x_out,x_p,y_p,m,n)

'Declare the variables as integer

DimiAsInteger

'Declare the variables as double

Dim x AsDouble,y(10)AsDouble,x_endAsDouble

Dim h AsDouble

'Set the variable m

m =0

'Store the value of x_i in x

x =x_i

'Use for loop to store different values of y_i in y

Fori=1To n

y(i)=y_i(i)

Nexti

'Store the value of x in x_p

x_p(m)= x

'Use for loop to store different values of y in y_p

Fori=1To n

y_p(m,i)= y(i)

Nexti

'Use the condition to find the next x values

Do

x_end= x +x_out

If(x_end>x_f)Thenx_end=x_f

h =diffx

'Call the Integrator function

CallIntegrator(x,y,h,n,x_end)

m = m +1

'Store the value of x in x_p

x_p(m)= x

'Use for loop to store different values of y in y_p

Fori=1To n

y_p(m,i)= y(i)

Nexti

'Use condition to exit the loop

If(x >=x_f)ThenExitDo

Loop

EndSub

'Define the subfunction Integrator

SubIntegrator(x,y,h,n,x_end)

'Declare the variables

Dim j AsInteger

Dimynew(10)AsDouble

'Use conditions for calculation

Do

If(x_end- x < h)Then h =x_end- x

'Call the RK4sys function

Call RK4Sys(x,y,h,n,ynew)

For j =1To n

'Store the different values of ynew in y

y(j)=ynew(j)

Next j

'Use condition to exit the loop

If(x >=x_end)ThenExitDo

Loop

EndSub

' create a subfunction RK4sys

Sub RK4Sys(x,y,h,n,ynew)

'Declare the variables as integer

Dim j AsInteger

'Declare the variables as double

Dimy_m(10)AsDouble,y_e(10)AsDouble

Dim k_1(10)AsDouble,k_2(10)AsDouble,k_3(10)AsDouble,k_4(10)AsDouble

Dimslope(10)

'Call the Derivs function

CallDerivs(x,y,k_1)

'Use for loop to store different values of y_m

For j =1To n

'Assign the different values of y(j) + k_1(j) * h / 2 to y_m

y_m(j)= y(j)+ k_1(j)* h /2

Next j

'Call the Derivs function

CallDerivs(x + h /2,y_m,k_2)

'Use for loop to store different values of y_m

For j =1To n

'Assign the different values of y(j) + k_2(j) * h / 2 to y_m

y_m(j)= y(j)+ k_2(j)* h /2

Next j

'Call the Derivs function

CallDerivs(x + h /2,y_m,k_3)

'Use for loop to store different values of y_e

For j =1To n

'Assign the different values of y(j) + k_3(j) * h to y_e

y_e(j)= y(j)+ k_3(j)* h

Next j

'Call the Derivs function

CallDerivs(x + h,y_e,k_4)

'Use for loop to store different values of slope

For j =1To n

'Assign the different value of k_1(j) + 2 * (k_2(j) + k_3(j)) + k_4(j)) / 6 to slope(j)

slope(j)=(k_1(j)+2*(k_2(j)+ k_3(j))+ k_4(j))/6

Next j

'Use for loop to store different values of ynew

For j =1To n

'Assign the different values of y(j) + slope(j) * h to ynew(j)

ynew(j)= y(j)+ slope(j)* h

Next j

'Write the next x value

x = x + h

EndSub

' Define the subfunction Derivs

SubDerivs(x,y,dydx)

'Write the ordinary differential equations

dydx(1)=-10* y(1)+10* y(2)

dydx(2)=28* y(1)- y(2)- y(1)* y(3)

dydx(3)=-2.66* y(3)+ y(1)* y(2)

EndSub

Output:

To draw the graph of the above results, follow the steps in excel sheet as given below,

Step 1: Select the cell from A4 to A205 and cell B4 to B205. Then, go to the Insert and select the scatter with smooth lines from the chart.

Step 2: Select the cell from A4 to A205 and cell C4 to C205. Then, go to the Insert and select the scatter with smooth lines from the chart.

Step 3: Select the cell from A4 to A205 and cell D4 to D205. Then, go to the Insert and select the scatter with smooth lines from the chart.

Step 4: Select one of the graphs and paste it on another graph to merge the graphs.

The graph obtained is,

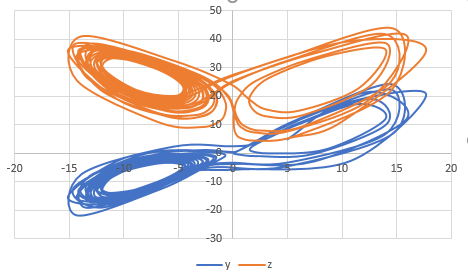
And, to draw the phase plane plot follow the steps as below,

Step 4: Select the column B, column C and column D. Then, go to the Insert and select the scatter with smooth lines from the chart.

The graph obtained is,

To determine

The solution of Lorentz equation $\frac{dx}{dt}=-10x+10y,\frac{dy}{dt}=28x-y-xz$ and $\frac{dz}{dt}=-2.666667z+xy$ by the MATLAB ode45 function with the step size of 0.1 from $t=0\text{ to }20$. Also plot the result and the phase-plane plot.

Answer to Problem 18P

Solution:

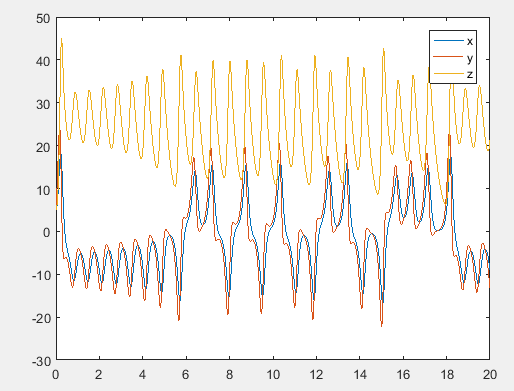
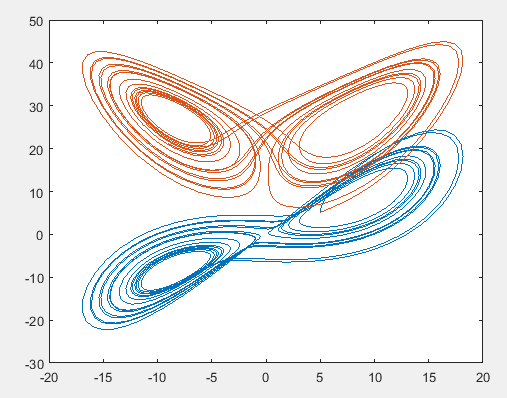
The solution graph of Lorentz equation is,

Explanation of Solution

Given Information:

Lorentz equations,

$\begin{array}{c}\frac{dx}{dt}=-10x+10y\\ \frac{dy}{dt}=28x-y-xz\\ \frac{dz}{dt}=-2.666667z+xy\end{array}$

and Initial conditions are $x=y=z=5$.

Consider the Lorentz equations,

$\begin{array}{c}\frac{dx}{dt}=-10x+10y\\ \frac{dy}{dt}=28x-y-xz\\ \frac{dz}{dt}=-2.666667z+xy\end{array}$

Use MATLAB ode45 function to solve the above differential functions as below,

Code:

%create the function lorenz

functionyp=lorenz(t, y)

%Write the equations

yp=[-10*y(1)+10*y(2);28*y(1)-y(2)-y(1)*y(3);-2.666667*y(3)+y(1)*y(2)];

Output:

The graph obtained as,

Write the command as below to plot the phase-plane,

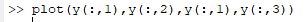
The phase plane graph obtained as,