
Sub part (a):
Diminishing marginal utility .
Sub part (a):
Explanation of Solution
The utility function is
Figure 1 illustrates the diminishing marginal utility.
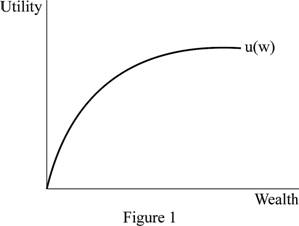
In Figure 1, the horizontal axis measures the quantity of wealth and the vertical axis measures the utility. When the quantity of wealth increases then the additional utility decreases.
Concept introduction:
Marginal utility: Marginal utility refers to the additional units of satisfaction derived from one more additional unit of goods and services.
Diminishing marginal utility: Diminishing marginal utility refers to a decrease in the additional satisfaction as a result of increasing the consumption.
Sub Part (b):
Expected value.
Sub Part (b):
Explanation of Solution
Since the value is sure, the probability is 1. Expected value of A can be calculated as follows:
Expected value of A is $4,000,000.
Expected value of B can be calculated as follows.
Expected value of B is $4,200,000. Thus, B offers higher value.
Concept introduction:
Risk is the future uncertainty about deviation from expected earnings or expected outcome. Risk measures the uncertainty situation that an investor is willing to take to realize a gain from an investment.
Risk aversion: Risk aversion can be defined as it is a dislike of an uncertainty.
Marginal utility: Marginal utility refers to the additional units of satisfaction derived from one more additional unit of goods and services.
Diminishing marginal utility: Diminishing marginal utility refers to a decrease in the additional satisfaction as a result of increasing the consumption.
Sub part (c):
Expected utility.
Sub part (c):
Explanation of Solution
Expected utility of A can be calculated as follows:
Expected utility of A is $2,000.
Expected utility of B can be calculated as follows.
Expected utility of B is $1,800.
Concept introduction:
Risk is the future uncertainty about deviation from expected earnings or expected outcome. Risk measures the uncertainty situation that an investor is willing to take to realize a gain from an investment.
Risk aversion: Risk aversion can be defined as it is a dislike of an uncertainty.
Marginal utility: Marginal utility refers to the additional units of satisfaction derived from one more additional unit of goods and services.
Diminishing marginal utility: Diminishing marginal utility refers to a decrease in the additional satisfaction as a result of increasing the consumption.
Sub part (d):
greaterExpected utility.
Sub part (d):
Explanation of Solution
Since the expected utility from B is greater than A, the person should select A.
Concept introduction:
Risk is the future uncertainty about deviation from expected earnings or expected outcome. Risk measures the uncertainty situation that an investor is willing to take to realize a gain from an investment.
Risk aversion: Risk aversion can be defined as it is a dislike of an uncertainty.
Marginal utility: Marginal utility refers to the additional units of satisfaction derived from one more additional unit of goods and services.
Diminishing marginal utility: Diminishing marginal utility refers to a decrease in the additional satisfaction as a result of increasing the consumption.
Want to see more full solutions like this?
Chapter 27 Solutions
PRINC OF ECONOMICS PKG >CUSTOM<
- You are the manager of a large automobile dealership who wants to learn more about the effective- ness of various discounts offered to customers over the past 14 months. Following are the average negotiated prices for each month and the quantities sold of a basic model (adjusted for various options) over this period of time. 1. Graph this information on a scatter plot. Estimate the demand equation. What do the regression results indicate about the desirability of discounting the price? Explain. Month Price Quantity Jan. 12,500 15 Feb. 12,200 17 Mar. 11,900 16 Apr. 12,000 18 May 11,800 20 June 12,500 18 July 11,700 22 Aug. 12,100 15 Sept. 11,400 22 Oct. 11,400 25 Nov. 11,200 24 Dec. 11,000 30 Jan. 10,800 25 Feb. 10,000 28 2. What other factors besides price might be included in this equation? Do you foresee any difficulty in obtaining these additional data or incorporating them in the regression analysis?arrow_forwardsimple steps on how it should look like on excelarrow_forwardConsider options on a stock that does not pay dividends.The stock price is $100 per share, and the risk-free interest rate is 10%.Thestock moves randomly with u=1.25and d=1/u Use Excel to calculate the premium of a10-year call with a strike of $100.arrow_forward
- Please solve this, no words or explanations.arrow_forward17. Given that C=$700+0.8Y, I=$300, G=$600, what is Y if Y=C+I+G?arrow_forwardUse the Feynman technique throughout. Assume that you’re explaining the answer to someone who doesn’t know the topic at all. Write explanation in paragraphs and if you use currency use USD currency: 10. What is the mechanism or process that allows the expenditure multiplier to “work” in theKeynesian Cross Model? Explain and show both mathematically and graphically. What isthe underpinning assumption for the process to transpire?arrow_forward
- Use the Feynman technique throughout. Assume that you’reexplaining the answer to someone who doesn’t know the topic at all. Write it all in paragraphs: 2. Give an overview of the equation of exchange (EoE) as used by Classical Theory. Now,carefully explain each variable in the EoE. What is meant by the “quantity theory of money”and how is it different from or the same as the equation of exchange?arrow_forwardZbsbwhjw8272:shbwhahwh Zbsbwhjw8272:shbwhahwh Zbsbwhjw8272:shbwhahwhZbsbwhjw8272:shbwhahwhZbsbwhjw8272:shbwhahwharrow_forwardUse the Feynman technique throughout. Assume that you’re explaining the answer to someone who doesn’t know the topic at all:arrow_forward
 Essentials of Economics (MindTap Course List)EconomicsISBN:9781337091992Author:N. Gregory MankiwPublisher:Cengage Learning
Essentials of Economics (MindTap Course List)EconomicsISBN:9781337091992Author:N. Gregory MankiwPublisher:Cengage Learning Brief Principles of Macroeconomics (MindTap Cours...EconomicsISBN:9781337091985Author:N. Gregory MankiwPublisher:Cengage Learning
Brief Principles of Macroeconomics (MindTap Cours...EconomicsISBN:9781337091985Author:N. Gregory MankiwPublisher:Cengage Learning Managerial Economics: A Problem Solving ApproachEconomicsISBN:9781337106665Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike ShorPublisher:Cengage Learning
Managerial Economics: A Problem Solving ApproachEconomicsISBN:9781337106665Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike ShorPublisher:Cengage Learning Economics (MindTap Course List)EconomicsISBN:9781337617383Author:Roger A. ArnoldPublisher:Cengage Learning
Economics (MindTap Course List)EconomicsISBN:9781337617383Author:Roger A. ArnoldPublisher:Cengage Learning





