
The following nonlinear, parasitic ODE was suggested by Hornbeck (1975):
If the initial condition is
(a) Analytically
(b) Using the fourth-order RK method with a constant step size of 0.03125.
(c) Using the MATLAB function ode45.
(d) Using the MATLAB function ode23s.
(e) Using the MATLAB function ode23tb.
Present your results in graphical form.
(a)
To calculate: The analytical solution of the nonlinear, parasitic ordinary differential equation,
Answer to Problem 27P
Solution:
The analytical solution of the differential equation is
Explanation of Solution
Given Information:
A nonlinear, parasitic ordinary differential equation,
Formula used:
The general linear differential equation is,
Calculation:
Consider the nonlinear ordinary differential equation,
Rearrange the above differential equationto get,
Now, compare the above differential equation with the general linear differential equation
Thus,
Now, find the integrating factor (I. F.) as shown below,
Therefore, the solution of the linear differential equation is given as,
Substitute the value of integrating factor (I. F.) in above equation,
Now, integrate the right-hand-side of the above equation,
Solve further, to get
Thus, the solution is
Now, to determine the constant c, use the initial condition
Substitute
Therefore,
Hence, the solution of the differential equation is
(b)
To calculate: Thesolution of the nonlinear, parasitic ordinary differential equation,
Answer to Problem 27P
Solution:
The graph of the solution of the differential equation is,
Explanation of Solution
Given Information:
A nonlinear, parasitic ordinary differential equation,
Calculation:
Consider the nonlinear ordinary differential equation,
The VBA code to solve the above differential equation with fourth-order RK method with a constant step size of 0.03125 is given below,
The output given below is obtained in the Excel after the execution of the above code:
| 4th order RK | ||
| t | y1 | |
| 0 | 0.08 | 0.08 |
| 0.03125 | 0.093476 | 0.093477 |
| 0.0625 | 0.108906 | 0.108906 |
| 0.09375 | 0.126289 | 0.126289 |
| 0.125 | 0.145625 | 0.145625 |
| 0.15625 | 0.166914 | 0.166914 |
| 0.1875 | 0.190156 | 0.190156 |
| 0.21875 | 0.215351 | 0.215352 |
| 0.25 | 0.242499 | 0.2425 |
| 0.28125 | 0.2716 | 0.271602 |
| 0.3125 | 0.302655 | 0.302656 |
| 0.34375 | 0.335662 | 0.335664 |
| 0.375 | 0.370622 | 0.370625 |
| 0.40625 | 0.407536 | 0.407539 |
| 0.4375 | 0.446403 | 0.446406 |
| 0.46875 | 0.487222 | 0.487227 |
| 0.5 | 0.529995 | 0.53 |
| 0.53125 | 0.57472 | 0.574727 |
| 0.5625 | 0.621399 | 0.621406 |
| 0.59375 | 0.670031 | 0.670039 |
| 0.625 | 0.720615 | 0.720625 |
| 0.65625 | 0.773152 | 0.773164 |
| 0.6875 | 0.827642 | 0.827656 |
| 0.71875 | 0.884085 | 0.884102 |
| 0.75 | 0.942481 | 0.9425 |
| 0.78125 | 1.002829 | 1.002852 |
| 0.8125 | 1.06513 | 1.065156 |
| 0.84375 | 1.129383 | 1.129414 |
| 0.875 | 1.195589 | 1.195625 |
| 0.90625 | 1.263747 | 1.263789 |
| 0.9375 | 1.333857 | 1.333906 |
| 0.96875 | 1.405919 | 1.405977 |
| 1 | 1.479932 | 1.48 |
| 1.03125 | 1.555897 | 1.555977 |
| 1.0625 | 1.633814 | 1.633906 |
| 1.09375 | 1.713681 | 1.713789 |
| 1.125 | 1.795498 | 1.795625 |
| 1.15625 | 1.879266 | 1.879414 |
| 1.1875 | 1.964983 | 1.965156 |
| 1.21875 | 2.052649 | 2.052852 |
| 1.25 | 2.142263 | 2.1425 |
| 1.28125 | 2.233824 | 2.234102 |
| 1.3125 | 2.327332 | 2.327656 |
| 1.34375 | 2.422785 | 2.423164 |
| 1.375 | 2.520181 | 2.520625 |
| 1.40625 | 2.61952 | 2.620039 |
| 1.4375 | 2.7208 | 2.721406 |
| 1.46875 | 2.824017 | 2.824727 |
| 1.5 | 2.929171 | 2.93 |
| 1.53125 | 3.036257 | 3.037227 |
| 1.5625 | 3.145273 | 3.146406 |
| 1.59375 | 3.256214 | 3.257539 |
| 1.625 | 3.369075 | 3.370625 |
| 1.65625 | 3.483852 | 3.485664 |
| 1.6875 | 3.600538 | 3.602656 |
| 1.71875 | 3.719125 | 3.721602 |
| 1.75 | 3.839605 | 3.8425 |
| 1.78125 | 3.961966 | 3.965352 |
| 1.8125 | 4.086198 | 4.090156 |
| 1.84375 | 4.212287 | 4.216914 |
| 1.875 | 4.340215 | 4.345625 |
| 1.90625 | 4.469964 | 4.476289 |
| 1.9375 | 4.601512 | 4.608906 |
| 1.96875 | 4.734831 | 4.743477 |
| 2 | 4.869893 | 4.88 |
| 2.03125 | 5.00666 | 5.018477 |
| 2.0625 | 5.145091 | 5.158906 |
| 2.09375 | 5.285137 | 5.301289 |
| 2.125 | 5.426742 | 5.445625 |
| 2.15625 | 5.569837 | 5.591914 |
| 2.1875 | 5.714346 | 5.740156 |
| 2.21875 | 5.860176 | 5.890352 |
| 2.25 | 6.007221 | 6.0425 |
| 2.28125 | 6.155356 | 6.196602 |
| 2.3125 | 6.304436 | 6.352656 |
| 2.34375 | 6.454288 | 6.510664 |
| 2.375 | 6.604715 | 6.670625 |
| 2.40625 | 6.755482 | 6.832539 |
| 2.4375 | 6.906318 | 6.996406 |
| 2.46875 | 7.056903 | 7.162227 |
| 2.5 | 7.206864 | 7.33 |
| 2.53125 | 7.355766 | 7.499727 |
| 2.5625 | 7.503099 | 7.671406 |
| 2.59375 | 7.648268 | 7.845039 |
| 2.625 | 7.790577 | 8.020625 |
| 2.65625 | 7.92921 | 8.198164 |
| 2.6875 | 8.063218 | 8.377656 |
| 2.71875 | 8.191486 | 8.559102 |
| 2.75 | 8.312714 | 8.7425 |
| 2.78125 | 8.425381 | 8.927852 |
| 2.8125 | 8.527709 | 9.115156 |
| 2.84375 | 8.617619 | 9.304414 |
| 2.875 | 8.69268 | 9.495625 |
| 2.90625 | 8.750052 | 9.688789 |
| 2.9375 | 8.786412 | 9.883906 |
| 2.96875 | 8.797877 | 10.08098 |
| 3 | 8.779905 | 10.28 |
| 3.03125 | 8.727189 | 10.48098 |
| 3.0625 | 8.633523 | 10.68391 |
| 3.09375 | 8.491649 | 10.88879 |
| 3.125 | 8.293087 | 11.09563 |
| 3.15625 | 8.027917 | 11.30441 |
| 3.1875 | 7.684546 | 11.51516 |
| 3.21875 | 7.249417 | 11.72785 |
| 3.25 | 6.706683 | 11.9425 |
| 3.28125 | 6.037815 | 12.1591 |
| 3.3125 | 5.221152 | 12.37766 |
| 3.34375 | 4.231369 | 12.59816 |
| 3.375 | 3.038857 | 12.82063 |
| 3.40625 | 1.609002 | 13.04504 |
| 3.4375 | -0.09867 | 13.27141 |
| 3.46875 | -2.13146 | 13.49973 |
| 3.5 | -4.5447 | 13.73 |
| 3.53125 | -7.40305 | 13.96223 |
| 3.5625 | -10.7821 | 14.19641 |
| 3.59375 | -14.7703 | 14.43254 |
| 3.625 | -19.4709 | 14.67063 |
| 3.65625 | -25.0048 | 14.91066 |
| 3.6875 | -31.5132 | 15.15266 |
| 3.71875 | -39.1613 | 15.3966 |
| 3.75 | -48.1421 | 15.6425 |
| 3.78125 | -58.6814 | 15.89035 |
| 3.8125 | -71.043 | 16.14016 |
| 3.84375 | -85.5354 | 16.39191 |
| 3.875 | -102.519 | 16.64563 |
| 3.90625 | -122.417 | 16.90129 |
| 3.9375 | -145.72 | 17.15891 |
| 3.96875 | -173.006 | 17.41848 |
| 4 | -204.949 | 17.68 |
| 4.03125 | -242.336 | 17.94348 |
| 4.0625 | -286.088 | 18.20891 |
| 4.09375 | -337.283 | 18.47629 |
| 4.125 | -397.179 | 18.74563 |
| 4.15625 | -467.248 | 19.01691 |
| 4.1875 | -549.211 | 19.29016 |
| 4.21875 | -645.079 | 19.56535 |
| 4.25 | -757.205 | 19.8425 |
| 4.28125 | -888.338 | 20.1216 |
| 4.3125 | -1041.69 | 20.40266 |
| 4.34375 | -1221.03 | 20.68566 |
| 4.375 | -1430.74 | 20.97063 |
| 4.40625 | -1675.96 | 21.25754 |
| 4.4375 | -1962.71 | 21.54641 |
| 4.46875 | -2297.99 | 21.83723 |
| 4.5 | -2690.02 | 22.13 |
| 4.53125 | -3148.39 | 22.42473 |
| 4.5625 | -3684.34 | 22.72141 |
| 4.59375 | -4310.97 | 23.02004 |
| 4.625 | -5043.62 | 23.32063 |
| 4.65625 | -5900.23 | 23.62316 |
| 4.6875 | -6901.75 | 23.92766 |
| 4.71875 | -8072.7 | 24.2341 |
| 4.75 | -9441.73 | 24.5425 |
| 4.78125 | -11042.3 | 24.85285 |
| 4.8125 | -12913.7 | 25.16516 |
| 4.84375 | -15101.5 | 25.47941 |
| 4.875 | -17659.5 | 25.79563 |
| 4.90625 | -20650.1 | 26.11379 |
| 4.9375 | -24146.4 | 26.43391 |
| 4.96875 | -28234.2 | 26.75598 |
Now, plot the following chart using the data obtained in Excel.
In the above plot, the series1 represent the numerical solution whereas the series2 represent the exact solution.
(c)
The solution of the nonlinear, parasitic ordinary differential equation,
Answer to Problem 27P
Solution:
The graph of the solution of the differential equation is,
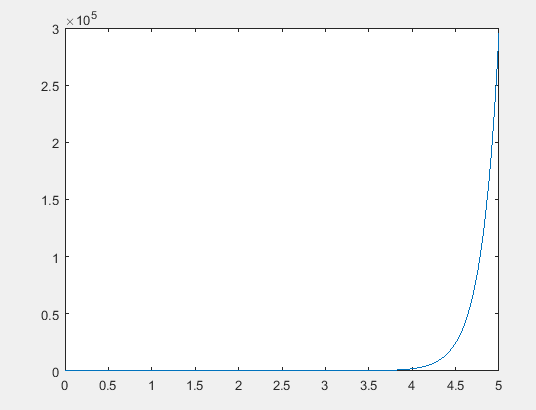
Explanation of Solution
Given Information:
A nonlinear, parasitic ordinary differential equation,
Consider the nonlinear ordinary differential equation,
Use the MATLAB function
Write the code given below in MATLAB editor window and save it.
function
Now, write the following code in MATLAB command window

Following graph is obtained after the execution of the above MATLAB code.

(d)
The solution of the nonlinear, parasitic ordinary differential equation,
Answer to Problem 27P
Solution:
The graph of the solution of the differential equation is,
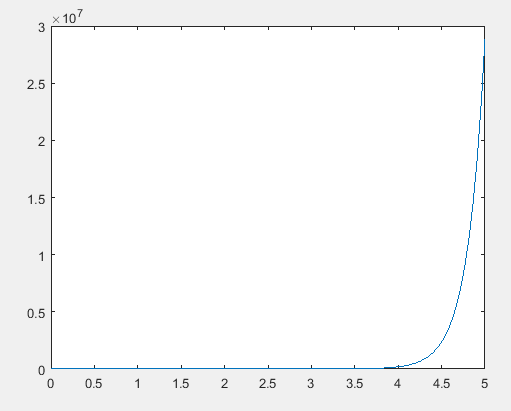
Explanation of Solution
Given Information:
A nonlinear, parasitic ordinary differential equation,
Consider the nonlinear ordinary differential equation,
Use the MATLAB function
Write the code given below in MATLAB editor window and save it.
function
Now, write the following code in MATLAB command window

Following graph is obtained after the execution of the above MATLAB code.

(e)
The solution of the nonlinear, parasitic ordinary differential equation,
Answer to Problem 27P
Solution:
The graph of the solution of the differential equation is,
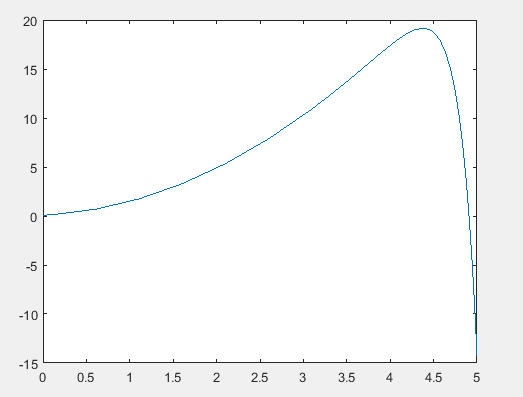
Explanation of Solution
Given Information:
A nonlinear, parasitic ordinary differential equation,
Consider the nonlinear ordinary differential equation,
Use the MATLAB function
Write the code given below in MATLAB editor window and save it.
function
Now, write the following code in MATLAB command window

Following graph is obtained after the execution of the above MATLAB code.

Want to see more full solutions like this?
Chapter 27 Solutions
Numerical Methods for Engineers
Additional Math Textbook Solutions
Introductory Statistics
Calculus: Early Transcendentals (2nd Edition)
Precalculus: A Unit Circle Approach (3rd Edition)
A First Course in Probability (10th Edition)
Precalculus: Mathematics for Calculus (Standalone Book)
Elementary Statistics ( 3rd International Edition ) Isbn:9781260092561
- 1. Evaluate the following improper integrals: (a) fe-rt dt; (b) fert dt; (c) fi da dxarrow_forward8. Given the rate of net investment I(t) = 9t¹/2, find the level of capital formation in (i) 16 years and (ii) between the 4th and the 8th years.arrow_forward9. If the marginal revenue function of a firm in the production of output is MR = 40 - 10q² where q is the level of output, and total revenue is 120 at 3 units of output, find the total revenue function. [Hints: TR = √ MRdq]arrow_forward
- 6. Solve the following first-order linear differential equations; if an initial condition is given, definitize the arbitrary constant: (a) 2 + 12y + 2et = 0, y(0) = /; (b) dy+y=tarrow_forward4. Let A = {a, b, c, d, e, f}, B = {e, f, g, h} and C = {a, e, h,i}. Let U = {a, b, c, d, e, f, g, h, i, j, k}. • Draw a Venn Diagram to describe the relationships between these sets Find (AB) NC • Find (AC) UB Find AUBUC • Find (BC) N (A - C)arrow_forward7. A consumer lives on an island where she produces two goods x and y according to the production possibility frontier x² + y² < 200 and she consumes all the goods. Her utility function is U(x, y) = x y³. She faces an environmental constraint on her total output of both goods. The environmental constraint is given by x + y ≤20. • (a) Write down the consumer's optimization problem. (b) Write out the Kuhn-Tucker first order conditions. (c) Find the consumer's optimal consumption bundle (x*, y*).arrow_forward
- 3. Answer the following questions: (a) Given the marginal propensity to import M'(Y) = 0.1 and the information that M = 20 when Y = 0, find the import function M(Y). (b) Given a continuous income stream at the constant rate of $1,000 per year, what will be the present value II if the income stream terminates after exactly 3 years and the discount rate is 0.04? (c) What is the present value of a perpetual cash flow of $2,460 per year, discounted at r = 8%?arrow_forward5. Let A and B be arbitrary sets. Prove AnB = AUB.arrow_forward2. Answer the following questions: (a) Given the marginal-revenue function R'(Q) = 28Q - €0.3Q, find the total-revenue function R(Q). What initial condition can you introduce to definitize the constant of integration? = (b) Given the marginal propensity to consume C'(Y) 0.80.1Y-1/2 and the information that C = Y when Y = 100, find the consumption function C(Y).arrow_forward
- 7. Let X, A, and B be arbitrary sets such that ACX and BC X. Prove AUB CX.arrow_forward1. Write out the following sets as a list of elements. If necessary you may use ... in your description. {x EZ: |x|< 10 A x < 0} {x ЄN: x ≤ 20 A x = 2y for some y = N} {n EN: 3 | n^ 1 < n < 20} {y Є Z: y² <0}arrow_forward3. For each statement below, write an equivalent statement using the justification given. = y Є A or yЄ B by the definition of union = y Є A or y Є B by the definition of set complement = x = C and x & D by DeMorgan's Law =Vx (x EnFxЄEUF) by definition of subset. = (X CYUZ)A (YUZ CX) by definition of set equalityarrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning


