
Concept explainers
(a)
The degree of precision.
Answer to Problem 1A
The degree of precision is
Explanation of Solution
Given information:
The number to calculate the degree of precision is
Draw the diagram to show the degree of precision.
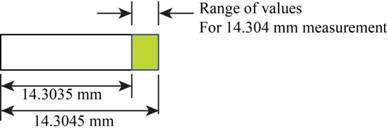
Figure-(I)
The degree of precision of a number depends upon the unit of measurement. Therefore, the degree of precision of number
Conclusion:
The degree of precision is
(b)
The value equal to or less than the range of the values.
Answer to Problem 1A
The value equal to or less than the range of the values is
Explanation of Solution
Write the expression for the value equal to less than the range of the values.
Here, the number is
Calculation:
Substitute
Conclusion:
The value equal to or less than the range of the values is
(c)
The value greater than the range of the values.
Answer to Problem 1A
The value greater than the range of the values is
Explanation of Solution
Write the expression for the value greater than the range of the values.
Here, the number is
Calculation:
Substitute
Conclusion:
The value greater than the range of the values is
Want to see more full solutions like this?
Chapter 27 Solutions
Mathematics for Machine Technology
- Convert 101101₂ to base 10arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward2) Prove that for all integers n > 1. dn 1 (2n)! 1 = dxn 1 - Ꮖ 4 n! (1-x)+/arrow_forward
- Definition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward3) Let a1, a2, and a3 be arbitrary real numbers, and define an = 3an 13an-2 + An−3 for all integers n ≥ 4. Prove that an = 1 - - - - - 1 - - (n − 1)(n − 2)a3 − (n − 1)(n − 3)a2 + = (n − 2)(n − 3)aı for all integers n > 1.arrow_forward
- Definition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL





