Pre-Algebra, Student Edition
Pre-Algebra, Student Edition
1st Edition
ISBN: 9780078885150
Author: McGraw-Hill
Publisher: Glencoe/McGraw-Hill
bartleby

Videos

Question
Book Icon
Chapter 2.6, Problem 49HP

a.

To determine

To check:whether the given statement is always, sometimes, or never true.

a.

Expert Solution
Check Mark

Answer to Problem 49HP

Never.

Explanation of Solution

Given:

The given statement is “Both x- coordinate and y- coordinate of a point in quadrant I are negative.

Calculation:

In quadrant I, all coordinates are positive. Therefore, both x- coordinate and y- coordinate of a point in quadrant I are positive.

Now, take an example, for coordinates (5,6) . Now draw the graph to check the quadrant.

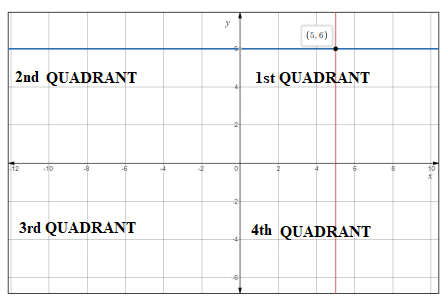
  Pre-Algebra, Student Edition, Chapter 2.6, Problem 49HP , additional homework tip 1

In labelling the quadrant,

The first quadrant is upper right section,

The second quadrant is upper left section,

The third quadrant is lower left section,

The forth quadrant islower right section.

Thus, the coordinate is located in 1st quadrant.

Hence, the statement is false.

b.

To determine

To check: whether the given statement is always, sometimes, or never true.

b.

Expert Solution
Check Mark

Answer to Problem 49HP

Sometimes.

Explanation of Solution

Given:

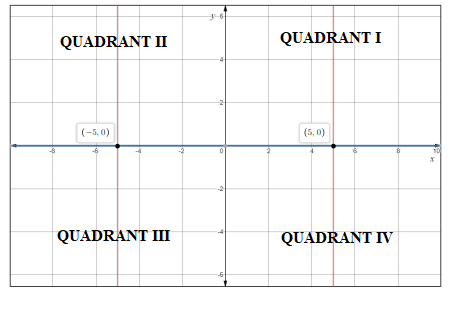
The given statement is "The x- coordinate of a point that liesx- axis is negative.

Calculation:

Both coordinate point lies on the x- axis.

The x- coordinate in quadrant I and II are positive whereas in III and IV are negative. So sometimes x- axis is positive or sometimes x- axis is negative.

Now, take an example, for coordinates (−5,0) and(5,0) .

  Pre-Algebra, Student Edition, Chapter 2.6, Problem 49HP , additional homework tip 2

Previous
Chapter 2.6, Problem 48HP
Next
Chapter 2.6, Problem 50HP

Chapter 2 Solutions

Pre-Algebra, Student Edition

Ch. 2.1 - Prob. 1ACYPCh. 2.1 - Prob. 1BCYPCh. 2.1 - Prob. 2ACYPCh. 2.1 - Prob. 2BCYPCh. 2.1 - Prob. 3CYPCh. 2.1 - Prob. 4ACYPCh. 2.1 - Prob. 4BCYPCh. 2.1 - Prob. 5CYPCh. 2.1 - Prob. 1CYUCh. 2.1 - Prob. 2CYU
Ch. 2.1 - Prob. 3CYUCh. 2.1 - Prob. 4CYUCh. 2.1 - Prob. 5CYUCh. 2.1 - Prob. 6CYUCh. 2.1 - Prob. 7CYUCh. 2.1 - Prob. 8CYUCh. 2.1 - Prob. 9CYUCh. 2.1 - Prob. 10CYUCh. 2.1 - Prob. 11CYUCh. 2.1 - Prob. 12CYUCh. 2.1 - Prob. 13CYUCh. 2.1 - Prob. 14CYUCh. 2.1 - Prob. 15CYUCh. 2.1 - Prob. 16PPSCh. 2.1 - Prob. 17PPSCh. 2.1 - Prob. 18PPSCh. 2.1 - Prob. 19PPSCh. 2.1 - Prob. 20PPSCh. 2.1 - Prob. 21PPSCh. 2.1 - Prob. 22PPSCh. 2.1 - Prob. 23PPSCh. 2.1 - Prob. 24PPSCh. 2.1 - Prob. 25PPSCh. 2.1 - Prob. 26PPSCh. 2.1 - Prob. 27PPSCh. 2.1 - Prob. 28PPSCh. 2.1 - Prob. 29PPSCh. 2.1 - Prob. 30PPSCh. 2.1 - Prob. 31PPSCh. 2.1 - Prob. 32PPSCh. 2.1 - Prob. 33PPSCh. 2.1 - Prob. 34PPSCh. 2.1 - Prob. 35PPSCh. 2.1 - Prob. 36PPSCh. 2.1 - Prob. 37PPSCh. 2.1 - Prob. 38PPSCh. 2.1 - Prob. 39PPSCh. 2.1 - Prob. 40PPSCh. 2.1 - Prob. 41PPSCh. 2.1 - Prob. 42PPSCh. 2.1 - Prob. 43PPSCh. 2.1 - Prob. 44PPSCh. 2.1 - Prob. 45PPSCh. 2.1 - Prob. 46PPSCh. 2.1 - Prob. 47PPSCh. 2.1 - Prob. 48PPSCh. 2.1 - Prob. 49PPSCh. 2.1 - Prob. 50PPSCh. 2.1 - Prob. 51PPSCh. 2.1 - Prob. 52PPSCh. 2.1 - Prob. 53PPSCh. 2.1 - Prob. 54PPSCh. 2.1 - Prob. 55PPSCh. 2.1 - Prob. 56PPSCh. 2.1 - Prob. 57PPSCh. 2.1 - Prob. 58PPSCh. 2.1 - Prob. 59PPSCh. 2.1 - Prob. 60PPSCh. 2.1 - Prob. 61PPSCh. 2.1 - Prob. 62PPSCh. 2.1 - Prob. 63PPSCh. 2.1 - Prob. 64HPCh. 2.1 - Prob. 65HPCh. 2.1 - Prob. 66HPCh. 2.1 - Prob. 67HPCh. 2.1 - Prob. 68HPCh. 2.1 - Prob. 69HPCh. 2.1 - Prob. 70HPCh. 2.1 - Prob. 71STPCh. 2.1 - Prob. 72STPCh. 2.1 - Prob. 73STPCh. 2.1 - Prob. 74STPCh. 2.1 - Prob. 75SRCh. 2.1 - Prob. 76SRCh. 2.1 - Prob. 77SRCh. 2.1 - Prob. 78SCh. 2.1 - Prob. 79SCh. 2.1 - Prob. 80SCh. 2.1 - Prob. 81SCh. 2.1 - Prob. 82SCh. 2.1 - Prob. 83SCh. 2.2 - Prob. 1ACYPCh. 2.2 - Prob. 1BCYPCh. 2.2 - Prob. 1CCYPCh. 2.2 - Prob. 2ACYPCh. 2.2 - Prob. 2BCYPCh. 2.2 - Prob. 3ACYPCh. 2.2 - Prob. 3BCYPCh. 2.2 - Prob. 4ACYPCh. 2.2 - Prob. 4BCYPCh. 2.2 - Prob. 5CYPCh. 2.2 - Prob. 6ACYPCh. 2.2 - Prob. 6BCYPCh. 2.2 - Prob. 1CYUCh. 2.2 - Prob. 2CYUCh. 2.2 - Prob. 3CYUCh. 2.2 - Prob. 4CYUCh. 2.2 - Prob. 5CYUCh. 2.2 - Prob. 6CYUCh. 2.2 - Prob. 7CYUCh. 2.2 - Prob. 8CYUCh. 2.2 - Prob. 9PPSCh. 2.2 - Prob. 10PPSCh. 2.2 - Prob. 11PPSCh. 2.2 - Prob. 12PPSCh. 2.2 - Prob. 13PPSCh. 2.2 - Prob. 14PPSCh. 2.2 - Prob. 15PPSCh. 2.2 - Prob. 16PPSCh. 2.2 - Prob. 17PPSCh. 2.2 - Prob. 18PPSCh. 2.2 - Prob. 19PPSCh. 2.2 - Prob. 20PPSCh. 2.2 - Prob. 21PPSCh. 2.2 - Prob. 22PPSCh. 2.2 - Prob. 23PPSCh. 2.2 - Prob. 24PPSCh. 2.2 - Prob. 25PPSCh. 2.2 - Prob. 26PPSCh. 2.2 - Prob. 27PPSCh. 2.2 - Prob. 28PPSCh. 2.2 - Prob. 29PPSCh. 2.2 - Prob. 30PPSCh. 2.2 - Prob. 31PPSCh. 2.2 - Prob. 32PPSCh. 2.2 - Prob. 33PPSCh. 2.2 - Prob. 34PPSCh. 2.2 - Prob. 35PPSCh. 2.2 - Prob. 36HPCh. 2.2 - Prob. 37HPCh. 2.2 - Prob. 38HPCh. 2.2 - Prob. 39HPCh. 2.2 - Prob. 40HPCh. 2.2 - Prob. 41HPCh. 2.2 - Prob. 42HPCh. 2.2 - Prob. 43HPCh. 2.2 - Prob. 44HPCh. 2.2 - Prob. 45STPCh. 2.2 - Prob. 46STPCh. 2.2 - Prob. 47STPCh. 2.2 - Prob. 48STPCh. 2.2 - Prob. 49SRCh. 2.2 - Prob. 50SRCh. 2.2 - Prob. 51SRCh. 2.2 - Prob. 52SRCh. 2.2 - Prob. 53SRCh. 2.2 - Prob. 54SRCh. 2.2 - Prob. 55SRCh. 2.2 - Prob. 56SRCh. 2.2 - Prob. 57SRCh. 2.2 - Prob. 58SRCh. 2.2 - Prob. 59SRCh. 2.2 - Prob. 60SRCh. 2.2 - Prob. 61SCh. 2.2 - Prob. 62SCh. 2.2 - Prob. 63SCh. 2.2 - Prob. 64SCh. 2.3 - Prob. 1ACYPCh. 2.3 - Prob. 1BCYPCh. 2.3 - Prob. 2ACYPCh. 2.3 - Prob. 2BCYPCh. 2.3 - Prob. 3CYPCh. 2.3 - Prob. 4ACYPCh. 2.3 - Prob. 4BCYPCh. 2.3 - Prob. 1CYUCh. 2.3 - Prob. 2CYUCh. 2.3 - Prob. 3CYUCh. 2.3 - Prob. 4CYUCh. 2.3 - Prob. 5CYUCh. 2.3 - Prob. 6CYUCh. 2.3 - Prob. 7CYUCh. 2.3 - Prob. 8CYUCh. 2.3 - Prob. 9CYUCh. 2.3 - Prob. 10CYUCh. 2.3 - Prob. 11CYUCh. 2.3 - Prob. 12CYUCh. 2.3 - Prob. 13PPSCh. 2.3 - Prob. 14PPSCh. 2.3 - Prob. 15PPSCh. 2.3 - Prob. 16PPSCh. 2.3 - Prob. 17PPSCh. 2.3 - Prob. 18PPSCh. 2.3 - Prob. 19PPSCh. 2.3 - Prob. 20PPSCh. 2.3 - Prob. 21PPSCh. 2.3 - Prob. 22PPSCh. 2.3 - Prob. 23PPSCh. 2.3 - Prob. 24PPSCh. 2.3 - Prob. 25PPSCh. 2.3 - Prob. 26PPSCh. 2.3 - Prob. 27PPSCh. 2.3 - Prob. 28PPSCh. 2.3 - Prob. 29PPSCh. 2.3 - Prob. 30PPSCh. 2.3 - Prob. 31PPSCh. 2.3 - Prob. 32PPSCh. 2.3 - Prob. 33PPSCh. 2.3 - Prob. 34PPSCh. 2.3 - Prob. 35PPSCh. 2.3 - Prob. 36PPSCh. 2.3 - Prob. 37PPSCh. 2.3 - Prob. 38PPSCh. 2.3 - Prob. 39PPSCh. 2.3 - Prob. 40PPSCh. 2.3 - Prob. 41HPCh. 2.3 - Prob. 42HPCh. 2.3 - Prob. 43HPCh. 2.3 - Prob. 44HPCh. 2.3 - Prob. 45STPCh. 2.3 - Prob. 46STPCh. 2.3 - Prob. 47STPCh. 2.3 - Prob. 48STPCh. 2.3 - Prob. 49SRCh. 2.3 - Prob. 50SRCh. 2.3 - Prob. 51SRCh. 2.3 - Prob. 52SRCh. 2.3 - Prob. 53SRCh. 2.3 - Prob. 54SRCh. 2.3 - Prob. 55SRCh. 2.3 - Prob. 56SRCh. 2.3 - Prob. 57SRCh. 2.3 - Prob. 58SCh. 2.3 - Prob. 59SCh. 2.3 - Prob. 60SCh. 2.3 - Prob. 61SCh. 2.4 - Prob. 1ACYPCh. 2.4 - Prob. 1BCYPCh. 2.4 - Prob. 2ACYPCh. 2.4 - Prob. 2BCYPCh. 2.4 - Prob. 3CYPCh. 2.4 - Prob. A4CYPCh. 2.4 - Prob. 4BCYPCh. 2.4 - Prob. 5ACYPCh. 2.4 - Prob. 5BCYPCh. 2.4 - Prob. 6ACYPCh. 2.4 - Prob. 6BCYPCh. 2.4 - Prob. 1CYUCh. 2.4 - Prob. 2CYUCh. 2.4 - Prob. 3CYUCh. 2.4 - Prob. 4CYUCh. 2.4 - Prob. 5CYUCh. 2.4 - Prob. 6CYUCh. 2.4 - Prob. 7CYUCh. 2.4 - Prob. 8CYUCh. 2.4 - Prob. 9CYUCh. 2.4 - Prob. 10CYUCh. 2.4 - Prob. 11PPSCh. 2.4 - Prob. 12PPSCh. 2.4 - Prob. 13PPSCh. 2.4 - Prob. 14PPSCh. 2.4 - Prob. 15PPSCh. 2.4 - Prob. 16PPSCh. 2.4 - Prob. 17PPSCh. 2.4 - Prob. 18PPSCh. 2.4 - Prob. 19PPSCh. 2.4 - Prob. 20PPSCh. 2.4 - Prob. 21PPSCh. 2.4 - Prob. 22PPSCh. 2.4 - Prob. 23PPSCh. 2.4 - Prob. 24PPSCh. 2.4 - Prob. 25PPSCh. 2.4 - Prob. 26PPSCh. 2.4 - Prob. 27PPSCh. 2.4 - Prob. 28PPSCh. 2.4 - Prob. 29PPSCh. 2.4 - Prob. 30PPSCh. 2.4 - Prob. 31PPSCh. 2.4 - Prob. 32PPSCh. 2.4 - Prob. 33PPSCh. 2.4 - Prob. 34PPSCh. 2.4 - Prob. 35PPSCh. 2.4 - Prob. 36PPSCh. 2.4 - Prob. 37PPSCh. 2.4 - Prob. 38PPSCh. 2.4 - Prob. 39PPSCh. 2.4 - Prob. 40PPSCh. 2.4 - Prob. 41PPSCh. 2.4 - Prob. 42PPSCh. 2.4 - Prob. 43HPCh. 2.4 - Prob. 44HPCh. 2.4 - Prob. 45HPCh. 2.4 - Prob. 46HPCh. 2.4 - Prob. 47HPCh. 2.4 - Prob. 48HPCh. 2.4 - Prob. 49HPCh. 2.4 - Prob. 50STPCh. 2.4 - Prob. 51STPCh. 2.4 - Prob. 52STPCh. 2.4 - Prob. 53STPCh. 2.4 - Prob. 54SRCh. 2.4 - Prob. 55SRCh. 2.4 - Prob. 56SRCh. 2.4 - Prob. 57SRCh. 2.4 - Prob. 58SRCh. 2.4 - Prob. 59SRCh. 2.4 - Prob. 60SCh. 2.4 - Prob. 61SCh. 2.4 - Prob. 62SCh. 2.4 - Prob. 63SCh. 2.5 - Prob. 1ACYPCh. 2.5 - Prob. 1BCYPCh. 2.5 - Prob. 2ACYPCh. 2.5 - Prob. 2BCYPCh. 2.5 - Prob. 3ACYPCh. 2.5 - Prob. 3BCYPCh. 2.5 - Prob. 4CYPCh. 2.5 - Prob. 1CYUCh. 2.5 - Prob. 2CYUCh. 2.5 - Prob. 3CYUCh. 2.5 - Prob. 4CYUCh. 2.5 - Prob. 5CYUCh. 2.5 - Prob. 6CYUCh. 2.5 - Prob. 7CYUCh. 2.5 - Prob. 8CYUCh. 2.5 - Prob. 9CYUCh. 2.5 - Prob. 10CYUCh. 2.5 - Prob. 11CYUCh. 2.5 - Prob. 12CYUCh. 2.5 - Prob. 13PPSCh. 2.5 - Prob. 14PPSCh. 2.5 - Prob. 15PPSCh. 2.5 - Prob. 16PPSCh. 2.5 - Prob. 17PPSCh. 2.5 - Prob. 18PPSCh. 2.5 - Prob. 19PPSCh. 2.5 - Prob. 20PPSCh. 2.5 - Prob. 21PPSCh. 2.5 - Prob. 22PPSCh. 2.5 - Prob. 23PPSCh. 2.5 - Prob. 24PPSCh. 2.5 - Prob. 25PPSCh. 2.5 - Prob. 26PPSCh. 2.5 - Prob. 27PPSCh. 2.5 - Prob. 28PPSCh. 2.5 - Prob. 29PPSCh. 2.5 - Prob. 30PPSCh. 2.5 - Prob. 31PPSCh. 2.5 - Prob. 32PPSCh. 2.5 - Prob. 33PPSCh. 2.5 - Prob. 34PPSCh. 2.5 - Prob. 35PPSCh. 2.5 - Prob. 36PPSCh. 2.5 - Prob. 37PPSCh. 2.5 - Prob. 38PPSCh. 2.5 - Prob. 39PPSCh. 2.5 - Prob. 40PPSCh. 2.5 - Prob. 41PPSCh. 2.5 - Prob. 42PPSCh. 2.5 - Prob. 43PPSCh. 2.5 - Prob. 44PPSCh. 2.5 - Prob. 45PPSCh. 2.5 - Prob. 46PPSCh. 2.5 - Prob. 47PPSCh. 2.5 - Prob. 48PPSCh. 2.5 - Prob. 49HPCh. 2.5 - Prob. 50HPCh. 2.5 - Prob. 51HPCh. 2.5 - Prob. 52HPCh. 2.5 - Prob. 53HPCh. 2.5 - Prob. 54STPCh. 2.5 - Prob. 55STPCh. 2.5 - Prob. 56STPCh. 2.5 - Prob. 57STPCh. 2.5 - Prob. 58SRCh. 2.5 - Prob. 59SRCh. 2.5 - Prob. 60SRCh. 2.5 - Prob. 61SRCh. 2.5 - Prob. 62SRCh. 2.5 - Prob. 63SRCh. 2.5 - Prob. 64SRCh. 2.5 - Prob. 65SRCh. 2.5 - Prob. 66SCh. 2.5 - Prob. 67SCh. 2.5 - Prob. 68SCh. 2.5 - Prob. 69SCh. 2.6 - Prob. 1ACYPCh. 2.6 - Prob. 1BCYPCh. 2.6 - Prob. 2ACYPCh. 2.6 - Prob. 2BCYPCh. 2.6 - Prob. 2CCYPCh. 2.6 - Prob. 3CYPCh. 2.6 - Prob. 1CYUCh. 2.6 - Prob. 2CYUCh. 2.6 - Prob. 3CYUCh. 2.6 - Prob. 4CYUCh. 2.6 - Prob. 5CYUCh. 2.6 - Prob. 6CYUCh. 2.6 - Prob. 7CYUCh. 2.6 - Prob. 8CYUCh. 2.6 - Prob. 9CYUCh. 2.6 - Prob. 10PPSCh. 2.6 - Prob. 11PPSCh. 2.6 - Prob. 12PPSCh. 2.6 - Prob. 13PPSCh. 2.6 - Prob. 14PPSCh. 2.6 - Prob. 15PPSCh. 2.6 - Prob. 16PPSCh. 2.6 - Prob. 17PPSCh. 2.6 - Prob. 18PPSCh. 2.6 - Prob. 19PPSCh. 2.6 - Prob. 20PPSCh. 2.6 - Prob. 21PPSCh. 2.6 - Prob. 22PPSCh. 2.6 - Prob. 23PPSCh. 2.6 - Prob. 24PPSCh. 2.6 - Prob. 25PPSCh. 2.6 - Prob. 26PPSCh. 2.6 - Prob. 27PPSCh. 2.6 - Prob. 28PPSCh. 2.6 - Prob. 29PPSCh. 2.6 - Prob. 30PPSCh. 2.6 - Prob. 31PPSCh. 2.6 - Prob. 32PPSCh. 2.6 - Prob. 33PPSCh. 2.6 - Prob. 34PPSCh. 2.6 - Prob. 35PPSCh. 2.6 - Prob. 36PPSCh. 2.6 - Prob. 37PPSCh. 2.6 - Prob. 38PPSCh. 2.6 - Prob. 39PPSCh. 2.6 - Prob. 40PPSCh. 2.6 - Prob. 41PPSCh. 2.6 - Prob. 42PPSCh. 2.6 - Prob. 43PPSCh. 2.6 - Prob. 44PPSCh. 2.6 - Prob. 45PPSCh. 2.6 - Prob. 46PPSCh. 2.6 - Prob. 47HPCh. 2.6 - Prob. 48HPCh. 2.6 - Prob. 49HPCh. 2.6 - Prob. 50HPCh. 2.6 - Prob. 51STPCh. 2.6 - Prob. 52STPCh. 2.6 - Prob. 53STPCh. 2.6 - Prob. 54STPCh. 2.6 - Prob. 55SRCh. 2.6 - Prob. 56SRCh. 2.6 - Prob. 57SRCh. 2.6 - Prob. 58SRCh. 2.6 - Prob. 59SRCh. 2.6 - Prob. 60SRCh. 2.6 - Prob. 61SRCh. 2.6 - Prob. 62SRCh. 2.6 - Prob. 63SCh. 2.6 - Prob. 64SCh. 2.6 - Prob. 65SCh. 2.6 - Prob. 66SCh. 2.6 - Prob. 67SCh. 2.6 - Prob. 68SCh. 2.7 - Prob. 1CYPCh. 2.7 - Prob. 2ACYPCh. 2.7 - Prob. 2BCYPCh. 2.7 - Prob. 1CYUCh. 2.7 - Prob. 2CYUCh. 2.7 - Prob. 3PPSCh. 2.7 - Prob. 4PPSCh. 2.7 - Prob. 5PPSCh. 2.7 - Prob. 6PPSCh. 2.7 - Prob. 7PPSCh. 2.7 - Prob. 8PPSCh. 2.7 - Prob. 9PPSCh. 2.7 - Prob. 10PPSCh. 2.7 - Prob. 11PPSCh. 2.7 - Prob. 12PPSCh. 2.7 - Prob. 13PPSCh. 2.7 - Prob. 14PPSCh. 2.7 - Prob. 15PPSCh. 2.7 - Prob. 16PPSCh. 2.7 - Prob. 17PPSCh. 2.7 - Prob. 18HPCh. 2.7 - Prob. 19HPCh. 2.7 - Prob. 20HPCh. 2.7 - Prob. 21HPCh. 2.7 - Prob. 22HPCh. 2.7 - Prob. 23STPCh. 2.7 - Prob. 24STPCh. 2.7 - Prob. 25STPCh. 2.7 - Prob. 26STPCh. 2.7 - Prob. 27SRCh. 2.7 - Prob. 28SRCh. 2.7 - Prob. 29SRCh. 2.7 - Prob. 30SRCh. 2.7 - Prob. 31SRCh. 2.7 - Prob. 32SRCh. 2.7 - Prob. 33SRCh. 2.7 - Prob. 34SCh. 2.7 - Prob. 35SCh. 2.7 - Prob. 36SCh. 2.7 - Prob. 37SCh. 2 - Prob. 1QCCh. 2 - Prob. 2QCCh. 2 - Prob. 3QCCh. 2 - Prob. 4QCCh. 2 - Prob. 5QCCh. 2 - Prob. 6QCCh. 2 - Prob. 7QCCh. 2 - Prob. 8QCCh. 2 - Prob. 9QCCh. 2 - Prob. 10QCCh. 2 - Prob. 11QCCh. 2 - Prob. 12QCCh. 2 - Prob. 13QCCh. 2 - Prob. 14QCCh. 2 - Prob. 15QCCh. 2 - Prob. 16QCCh. 2 - Prob. 1MCQCh. 2 - Prob. 2MCQCh. 2 - Prob. 3MCQCh. 2 - Prob. 4MCQCh. 2 - Prob. 5MCQCh. 2 - Prob. 6MCQCh. 2 - Prob. 7MCQCh. 2 - Prob. 8MCQCh. 2 - Prob. 9MCQCh. 2 - Prob. 10MCQCh. 2 - Prob. 11MCQCh. 2 - Prob. 12MCQCh. 2 - Prob. 13MCQCh. 2 - Prob. 14MCQCh. 2 - Prob. 15MCQCh. 2 - Prob. 16MCQCh. 2 - Prob. 17MCQCh. 2 - Prob. 18MCQCh. 2 - Prob. 19MCQCh. 2 - Prob. 20MCQCh. 2 - Prob. 21MCQCh. 2 - Prob. 22MCQCh. 2 - Prob. 23MCQCh. 2 - Prob. 24MCQCh. 2 - Prob. 25MCQCh. 2 - Prob. 1SGRCh. 2 - Prob. 2SGRCh. 2 - Prob. 3SGRCh. 2 - Prob. 4SGRCh. 2 - Prob. 5SGRCh. 2 - Prob. 6SGRCh. 2 - Prob. 7SGRCh. 2 - Prob. 8SGRCh. 2 - Prob. 9SGRCh. 2 - Prob. 10SGRCh. 2 - Prob. 11SGRCh. 2 - Prob. 12SGRCh. 2 - Prob. 13SGRCh. 2 - Prob. 14SGRCh. 2 - Prob. 15SGRCh. 2 - Prob. 16SGRCh. 2 - Prob. 17SGRCh. 2 - Prob. 18SGRCh. 2 - Prob. 19SGRCh. 2 - Prob. 20SGRCh. 2 - Prob. 21SGRCh. 2 - Prob. 22SGRCh. 2 - Prob. 23SGRCh. 2 - Prob. 24SGRCh. 2 - Prob. 25SGRCh. 2 - Prob. 26SGRCh. 2 - Prob. 27SGRCh. 2 - Prob. 28SGRCh. 2 - Prob. 29SGRCh. 2 - Prob. 30SGRCh. 2 - Prob. 31SGRCh. 2 - Prob. 32SGRCh. 2 - Prob. 33SGRCh. 2 - Prob. 34SGRCh. 2 - Prob. 35SGRCh. 2 - Prob. 36SGRCh. 2 - Prob. 37SGRCh. 2 - Prob. 38SGRCh. 2 - Prob. 39SGRCh. 2 - Prob. 40SGRCh. 2 - Prob. 41SGRCh. 2 - Prob. 42SGRCh. 2 - Prob. 43SGRCh. 2 - Prob. 44SGRCh. 2 - Prob. 45SGRCh. 2 - Prob. 46SGRCh. 2 - Prob. 47SGRCh. 2 - Prob. 48SGRCh. 2 - Prob. 49SGRCh. 2 - Prob. 50SGRCh. 2 - Prob. 51SGRCh. 2 - Prob. 52SGRCh. 2 - Prob. 53SGRCh. 2 - Prob. 54SGRCh. 2 - Prob. 55SGRCh. 2 - Prob. 56SGRCh. 2 - Prob. 57SGRCh. 2 - Prob. 58SGRCh. 2 - Prob. 59SGRCh. 2 - Prob. 60SGRCh. 2 - Prob. 61SGRCh. 2 - Prob. 1PTCh. 2 - Prob. 2PTCh. 2 - Prob. 3PTCh. 2 - Prob. 4PTCh. 2 - Prob. 5PTCh. 2 - Prob. 6PTCh. 2 - Prob. 7PTCh. 2 - Prob. 8PTCh. 2 - Prob. 9PTCh. 2 - Prob. 10PTCh. 2 - Prob. 11PTCh. 2 - Prob. 12PTCh. 2 - Prob. 13PTCh. 2 - Prob. 14PTCh. 2 - Prob. 15PTCh. 2 - Prob. 16PTCh. 2 - Prob. 17PTCh. 2 - Prob. 18PTCh. 2 - Prob. 19PTCh. 2 - Prob. 20PTCh. 2 - Prob. 21PTCh. 2 - Prob. 22PTCh. 2 - Prob. 23PTCh. 2 - Prob. 24PTCh. 2 - Prob. 25PTCh. 2 - Prob. 26PTCh. 2 - Prob. 27PTCh. 2 - Prob. 28PTCh. 2 - Prob. 29PTCh. 2 - Prob. 30PTCh. 2 - Prob. 31PTCh. 2 - Prob. 32PTCh. 2 - Prob. 33PTCh. 2 - Prob. 1ECh. 2 - Prob. 2ECh. 2 - Prob. 3ECh. 2 - Prob. 4ECh. 2 - Prob. 5ECh. 2 - Prob. 1STPCh. 2 - Prob. 2STPCh. 2 - Prob. 3STPCh. 2 - Prob. 4STPCh. 2 - Prob. 5STPCh. 2 - Prob. 6STPCh. 2 - Prob. 7STPCh. 2 - Prob. 8STPCh. 2 - Prob. 9STPCh. 2 - Prob. 10STPCh. 2 - Prob. 11STPCh. 2 - Prob. 12STPCh. 2 - Prob. 13STPCh. 2 - Prob. 14STP

Additional Math Textbook Solutions

Find more solutions based on key concepts
Fill in each blank so that the resulting statement is true. An equation that expresses a relationship between t...

Algebra and Trigonometry (6th Edition)

CHECK POINT I Let p and q represent the following statements: p : 3 + 5 = 8 q : 2 × 7 = 20. Determine the truth...

Thinking Mathematically (6th Edition)

Assessment 71A Write each of the following as a sum in expanded place value form. a. 0.023 b. 206.06 c. 312.010...

A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)

A student has to sell 2 books from a collection of 6 math, 7 science, and 4 economics books. How many choices a...

A First Course in Probability (10th Edition)

Use the shell method to find the volumes of the solids generated by revolving the regions bounded by the curves...

University Calculus: Early Transcendentals (4th Edition)

Second derivatives Find d2ydx2. 35. e2y + x = y

Calculus: Early Transcendentals (2nd Edition)

Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Text book image
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Text book image
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Text book image
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
Text book image
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
SEE MORE TEXTBOOKS
Basic Reflection Trigonometric Identity; Author: Anil kumar;https://www.youtube.com/watch?v=y-EGUD49fmw;License: Standard YouTube License, CC-BY