
(a)
A spreadsheet for
(a)
Answer to Problem 46AP
A spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.015932 | 25.1067 |
| 0.405 | 0.019602 | 20.66116 |
| 0.41 | 0.024117 | 17.00046 |
| 0.415 | 0.029673 | 13.98578 |
| 0.42 | 0.036508 | 11.50433 |
| 0.425 | 0.044918 | 9.461686 |
| 0.43 | 0.055264 | 7.780834 |
| 0.435 | 0.067995 | 6.397529 |
| 0.44 | 0.083657 | 5.259572 |
| 0.445 | 0.102927 | 4.323453 |
| 0.45 | 0.126637 | 3.553464 |
| 0.455 | 0.155807 | 2.92028 |
| 0.46 | 0.191697 | 2.39962 |
| 0.465 | 0.235855 | 1.97155 |
| 0.47 | 0.290184 | 1.619662 |
| 0.475 | 0.357027 | 1.330432 |
| 0.48 | 0.439268 | 1.092727 |
| 0.485 | 0.540454 | 0.897394 |
| 0.495 | 0.818117 | 0.605048 |
| 0.5 | 1.006569 | 0.496737 |
| 0.505 | 1.238432 | 0.407774 |
| 0.51 | 1.523704 | 0.334711 |
| 0.515 | 1.874688 | 0.274712 |
| 0.52 | 2.306521 | 0.225448 |
| 0.525 | 2.837827 | 0.185001 |
| 0.53 | 3.491518 | 0.151796 |
| 0.535 | 4.295787 | 0.124541 |
| 0.54 | 5.285319 | 0.10217 |
| 0.545 | 6.502788 | 0.08381 |
| 0.55 | 8.000701 | 0.068744 |
| 0.555 | 9.843657 | 0.056381 |
| 0.56 | 12.11114 | 0.046238 |
| 0.565 | 14.90093 | 0.037917 |
| 0.57 | 18.33335 | 0.031091 |
| 0.575 | 22.55642 | 0.025492 |
| 0.58 | 27.75228 | 0.020899 |
| 0.585 | 34.145 | 0.017133 |
| 0.59 | 42.01028 | 0.014044 |
| 0.595 | 51.68732 | 0.011512 |
| 0.6 | 63.59346 | 0.009435 |
A spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.005274 | 75.84672 |
| 0.405 | 0.0064 | 63.28565 |
| 0.41 | 0.007766 | 52.79679 |
| 0.415 | 0.009423 | 44.03979 |
| 0.42 | 0.011435 | 36.72991 |
| 0.425 | 0.013876 | 30.62901 |
| 0.43 | 0.016838 | 25.53795 |
| 0.435 | 0.020432 | 21.29022 |
| 0.44 | 0.024793 | 17.74668 |
| 0.445 | 0.030086 | 14.79101 |
| 0.45 | 0.036508 | 12.32605 |
| 0.455 | 0.044301 | 10.27061 |
| 0.46 | 0.053758 | 8.556892 |
| 0.465 | 0.065233 | 7.128278 |
| 0.47 | 0.079158 | 5.937492 |
| 0.475 | 0.096055 | 4.945067 |
| 0.48 | 0.11656 | 4.118066 |
| 0.485 | 0.141441 | 3.428998 |
| 0.495 | 0.20827 | 2.376718 |
| 0.5 | 0.252728 | 1.978408 |
| 0.505 | 0.306677 | 1.646686 |
| 0.51 | 0.372141 | 1.370449 |
| 0.515 | 0.451579 | 1.140443 |
| 0.52 | 0.547974 | 0.948949 |
| 0.525 | 0.664947 | 0.789537 |
| 0.53 | 0.806888 | 0.656844 |
| 0.535 | 0.979129 | 0.546404 |
| 0.54 | 1.188137 | 0.454493 |
| 0.545 | 1.44176 | 0.37801 |
| 0.55 | 1.749522 | 0.314372 |
| 0.555 | 2.122981 | 0.261425 |
| 0.56 | 2.576159 | 0.217378 |
| 0.565 | 3.126073 | 0.180738 |
| 0.57 | 3.793374 | 0.150262 |
| 0.575 | 4.603119 | 0.124915 |
| 0.58 | 5.585715 | 0.103836 |
| 0.585 | 6.778058 | 0.086308 |
| 0.59 | 8.224923 | 0.071733 |
| 0.595 | 9.98064 | 0.059615 |
| 0.6 | 12.11114 | 0.049541 |
A spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.002004 | 199.5582 |
| 0.405 | 0.002403 | 168.5349 |
| 0.41 | 0.002881 | 142.3127 |
| 0.415 | 0.003454 | 120.1526 |
| 0.42 | 0.004141 | 101.4283 |
| 0.425 | 0.004964 | 85.60991 |
| 0.43 | 0.005952 | 72.24847 |
| 0.435 | 0.007135 | 60.96416 |
| 0.44 | 0.008554 | 51.43551 |
| 0.445 | 0.010256 | 43.39059 |
| 0.45 | 0.012295 | 36.59933 |
| 0.455 | 0.014741 | 30.86719 |
| 0.46 | 0.017672 | 26.02967 |
| 0.465 | 0.021187 | 21.9477 |
| 0.47 | 0.0254 | 18.50372 |
| 0.475 | 0.030452 | 15.59839 |
| 0.48 | 0.036508 | 13.14778 |
| 0.485 | 0.043769 | 11.08098 |
| 0.495 | 0.062909 | 7.868498 |
| 0.5 | 0.07542 | 6.629515 |
| 0.505 | 0.09042 | 5.585066 |
| 0.51 | 0.108402 | 4.704703 |
| 0.515 | 0.129961 | 3.962729 |
| 0.52 | 0.155807 | 3.337456 |
| 0.525 | 0.186794 | 2.810585 |
| 0.53 | 0.223943 | 2.366674 |
| 0.535 | 0.26848 | 1.992698 |
| 0.54 | 0.321875 | 1.67767 |
| 0.545 | 0.385889 | 1.412324 |
| 0.55 | 0.462633 | 1.188846 |
| 0.555 | 0.554641 | 1.000647 |
| 0.56 | 0.664947 | 0.842173 |
| 0.565 | 0.79719 | 0.70874 |
| 0.57 | 0.955733 | 0.596401 |
| 0.575 | 1.145807 | 0.50183 |
| 0.58 | 1.373682 | 0.422223 |
| 0.585 | 1.646877 | 0.355218 |
| 0.59 | 1.974404 | 0.298824 |
| 0.595 | 2.367069 | 0.251366 |
| 0.6 | 2.837827 | 0.211429 |
Explanation of Solution
Given information: Th first symbol i.e. Euler’s number is
It is given that the expression for the current-voltage characteristic curve for a semiconductor diode as a function of temperature
Here,
Formula to calculate the resistance across the diode is,
Here,
The value of magnitude of electron charge is
The value of Boltzmann’s constant is
The value of voltage across the diode varies from
From equation (1), formula to calculate the current across a semiconductor diode temperature
Here,
Substitute
Thus, the current across a semiconductor diode temperature
From equation (2), formula to calculate the resistance across the diode is,
Here,
Substitute
Thus, the resistance across the diode is
As the value of voltage across the diode varies from
Thus, a spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.015932 | 25.1067 |
| 0.405 | 0.019602 | 20.66116 |
| 0.41 | 0.024117 | 17.00046 |
| 0.415 | 0.029673 | 13.98578 |
| 0.42 | 0.036508 | 11.50433 |
| 0.425 | 0.044918 | 9.461686 |
| 0.43 | 0.055264 | 7.780834 |
| 0.435 | 0.067995 | 6.397529 |
| 0.44 | 0.083657 | 5.259572 |
| 0.445 | 0.102927 | 4.323453 |
| 0.45 | 0.126637 | 3.553464 |
| 0.455 | 0.155807 | 2.92028 |
| 0.46 | 0.191697 | 2.39962 |
| 0.465 | 0.235855 | 1.97155 |
| 0.47 | 0.290184 | 1.619662 |
| 0.475 | 0.357027 | 1.330432 |
| 0.48 | 0.439268 | 1.092727 |
| 0.485 | 0.540454 | 0.897394 |
| 0.495 | 0.818117 | 0.605048 |
| 0.5 | 1.006569 | 0.496737 |
| 0.505 | 1.238432 | 0.407774 |
| 0.51 | 1.523704 | 0.334711 |
| 0.515 | 1.874688 | 0.274712 |
| 0.52 | 2.306521 | 0.225448 |
| 0.525 | 2.837827 | 0.185001 |
| 0.53 | 3.491518 | 0.151796 |
| 0.535 | 4.295787 | 0.124541 |
| 0.54 | 5.285319 | 0.10217 |
| 0.545 | 6.502788 | 0.08381 |
| 0.55 | 8.000701 | 0.068744 |
| 0.555 | 9.843657 | 0.056381 |
| 0.56 | 12.11114 | 0.046238 |
| 0.565 | 14.90093 | 0.037917 |
| 0.57 | 18.33335 | 0.031091 |
| 0.575 | 22.55642 | 0.025492 |
| 0.58 | 27.75228 | 0.020899 |
| 0.585 | 34.145 | 0.017133 |
| 0.59 | 42.01028 | 0.014044 |
| 0.595 | 51.68732 | 0.011512 |
| 0.6 | 63.59346 | 0.009435 |
From equation (1), formula to calculate the current across a semiconductor diode temperature
Here,
Substitute
Thus, the current across a semiconductor diode temperature
From equation (2), formula to calculate the resistance across the diode is,
Here,
Substitute
Thus, the resistance across the diode is
As the value of voltage across the diode varies from
Thus, a spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.005274 | 75.84672 |
| 0.405 | 0.0064 | 63.28565 |
| 0.41 | 0.007766 | 52.79679 |
| 0.415 | 0.009423 | 44.03979 |
| 0.42 | 0.011435 | 36.72991 |
| 0.425 | 0.013876 | 30.62901 |
| 0.43 | 0.016838 | 25.53795 |
| 0.435 | 0.020432 | 21.29022 |
| 0.44 | 0.024793 | 17.74668 |
| 0.445 | 0.030086 | 14.79101 |
| 0.45 | 0.036508 | 12.32605 |
| 0.455 | 0.044301 | 10.27061 |
| 0.46 | 0.053758 | 8.556892 |
| 0.465 | 0.065233 | 7.128278 |
| 0.47 | 0.079158 | 5.937492 |
| 0.475 | 0.096055 | 4.945067 |
| 0.48 | 0.11656 | 4.118066 |
| 0.485 | 0.141441 | 3.428998 |
| 0.495 | 0.20827 | 2.376718 |
| 0.5 | 0.252728 | 1.978408 |
| 0.505 | 0.306677 | 1.646686 |
| 0.51 | 0.372141 | 1.370449 |
| 0.515 | 0.451579 | 1.140443 |
| 0.52 | 0.547974 | 0.948949 |
| 0.525 | 0.664947 | 0.789537 |
| 0.53 | 0.806888 | 0.656844 |
| 0.535 | 0.979129 | 0.546404 |
| 0.54 | 1.188137 | 0.454493 |
| 0.545 | 1.44176 | 0.37801 |
| 0.55 | 1.749522 | 0.314372 |
| 0.555 | 2.122981 | 0.261425 |
| 0.56 | 2.576159 | 0.217378 |
| 0.565 | 3.126073 | 0.180738 |
| 0.57 | 3.793374 | 0.150262 |
| 0.575 | 4.603119 | 0.124915 |
| 0.58 | 5.585715 | 0.103836 |
| 0.585 | 6.778058 | 0.086308 |
| 0.59 | 8.224923 | 0.071733 |
| 0.595 | 9.98064 | 0.059615 |
| 0.6 | 12.11114 | 0.049541 |
From equation (1), formula to calculate the current across a semiconductor diode temperature
Here,
Substitute
Thus, the current across a semiconductor diode temperature
From equation (2), formula to calculate the resistance across the diode is,
Here,
Substitute
Thus, the resistance across the diode is
As the value of voltage across the diode varies from
Thus, a spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.002004 | 199.5582 |
| 0.405 | 0.002403 | 168.5349 |
| 0.41 | 0.002881 | 142.3127 |
| 0.415 | 0.003454 | 120.1526 |
| 0.42 | 0.004141 | 101.4283 |
| 0.425 | 0.004964 | 85.60991 |
| 0.43 | 0.005952 | 72.24847 |
| 0.435 | 0.007135 | 60.96416 |
| 0.44 | 0.008554 | 51.43551 |
| 0.445 | 0.010256 | 43.39059 |
| 0.45 | 0.012295 | 36.59933 |
| 0.455 | 0.014741 | 30.86719 |
| 0.46 | 0.017672 | 26.02967 |
| 0.465 | 0.021187 | 21.9477 |
| 0.47 | 0.0254 | 18.50372 |
| 0.475 | 0.030452 | 15.59839 |
| 0.48 | 0.036508 | 13.14778 |
| 0.485 | 0.043769 | 11.08098 |
| 0.495 | 0.062909 | 7.868498 |
| 0.5 | 0.07542 | 6.629515 |
| 0.505 | 0.09042 | 5.585066 |
| 0.51 | 0.108402 | 4.704703 |
| 0.515 | 0.129961 | 3.962729 |
| 0.52 | 0.155807 | 3.337456 |
| 0.525 | 0.186794 | 2.810585 |
| 0.53 | 0.223943 | 2.366674 |
| 0.535 | 0.26848 | 1.992698 |
| 0.54 | 0.321875 | 1.67767 |
| 0.545 | 0.385889 | 1.412324 |
| 0.55 | 0.462633 | 1.188846 |
| 0.555 | 0.554641 | 1.000647 |
| 0.56 | 0.664947 | 0.842173 |
| 0.565 | 0.79719 | 0.70874 |
| 0.57 | 0.955733 | 0.596401 |
| 0.575 | 1.145807 | 0.50183 |
| 0.58 | 1.373682 | 0.422223 |
| 0.585 | 1.646877 | 0.355218 |
| 0.59 | 1.974404 | 0.298824 |
| 0.595 | 2.367069 | 0.251366 |
| 0.6 | 2.837827 | 0.211429 |
Conclusion:
Therefore, a spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.015932 | 25.1067 |
| 0.405 | 0.019602 | 20.66116 |
| 0.41 | 0.024117 | 17.00046 |
| 0.415 | 0.029673 | 13.98578 |
| 0.42 | 0.036508 | 11.50433 |
| 0.425 | 0.044918 | 9.461686 |
| 0.43 | 0.055264 | 7.780834 |
| 0.435 | 0.067995 | 6.397529 |
| 0.44 | 0.083657 | 5.259572 |
| 0.445 | 0.102927 | 4.323453 |
| 0.45 | 0.126637 | 3.553464 |
| 0.455 | 0.155807 | 2.92028 |
| 0.46 | 0.191697 | 2.39962 |
| 0.465 | 0.235855 | 1.97155 |
| 0.47 | 0.290184 | 1.619662 |
| 0.475 | 0.357027 | 1.330432 |
| 0.48 | 0.439268 | 1.092727 |
| 0.485 | 0.540454 | 0.897394 |
| 0.495 | 0.818117 | 0.605048 |
| 0.5 | 1.006569 | 0.496737 |
| 0.505 | 1.238432 | 0.407774 |
| 0.51 | 1.523704 | 0.334711 |
| 0.515 | 1.874688 | 0.274712 |
| 0.52 | 2.306521 | 0.225448 |
| 0.525 | 2.837827 | 0.185001 |
| 0.53 | 3.491518 | 0.151796 |
| 0.535 | 4.295787 | 0.124541 |
| 0.54 | 5.285319 | 0.10217 |
| 0.545 | 6.502788 | 0.08381 |
| 0.55 | 8.000701 | 0.068744 |
| 0.555 | 9.843657 | 0.056381 |
| 0.56 | 12.11114 | 0.046238 |
| 0.565 | 14.90093 | 0.037917 |
| 0.57 | 18.33335 | 0.031091 |
| 0.575 | 22.55642 | 0.025492 |
| 0.58 | 27.75228 | 0.020899 |
| 0.585 | 34.145 | 0.017133 |
| 0.59 | 42.01028 | 0.014044 |
| 0.595 | 51.68732 | 0.011512 |
| 0.6 | 63.59346 | 0.009435 |
A spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.005274 | 75.84672 |
| 0.405 | 0.0064 | 63.28565 |
| 0.41 | 0.007766 | 52.79679 |
| 0.415 | 0.009423 | 44.03979 |
| 0.42 | 0.011435 | 36.72991 |
| 0.425 | 0.013876 | 30.62901 |
| 0.43 | 0.016838 | 25.53795 |
| 0.435 | 0.020432 | 21.29022 |
| 0.44 | 0.024793 | 17.74668 |
| 0.445 | 0.030086 | 14.79101 |
| 0.45 | 0.036508 | 12.32605 |
| 0.455 | 0.044301 | 10.27061 |
| 0.46 | 0.053758 | 8.556892 |
| 0.465 | 0.065233 | 7.128278 |
| 0.47 | 0.079158 | 5.937492 |
| 0.475 | 0.096055 | 4.945067 |
| 0.48 | 0.11656 | 4.118066 |
| 0.485 | 0.141441 | 3.428998 |
| 0.495 | 0.20827 | 2.376718 |
| 0.5 | 0.252728 | 1.978408 |
| 0.505 | 0.306677 | 1.646686 |
| 0.51 | 0.372141 | 1.370449 |
| 0.515 | 0.451579 | 1.140443 |
| 0.52 | 0.547974 | 0.948949 |
| 0.525 | 0.664947 | 0.789537 |
| 0.53 | 0.806888 | 0.656844 |
| 0.535 | 0.979129 | 0.546404 |
| 0.54 | 1.188137 | 0.454493 |
| 0.545 | 1.44176 | 0.37801 |
| 0.55 | 1.749522 | 0.314372 |
| 0.555 | 2.122981 | 0.261425 |
| 0.56 | 2.576159 | 0.217378 |
| 0.565 | 3.126073 | 0.180738 |
| 0.57 | 3.793374 | 0.150262 |
| 0.575 | 4.603119 | 0.124915 |
| 0.58 | 5.585715 | 0.103836 |
| 0.585 | 6.778058 | 0.086308 |
| 0.59 | 8.224923 | 0.071733 |
| 0.595 | 9.98064 | 0.059615 |
| 0.6 | 12.11114 | 0.049541 |
A spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.002004 | 199.5582 |
| 0.405 | 0.002403 | 168.5349 |
| 0.41 | 0.002881 | 142.3127 |
| 0.415 | 0.003454 | 120.1526 |
| 0.42 | 0.004141 | 101.4283 |
| 0.425 | 0.004964 | 85.60991 |
| 0.43 | 0.005952 | 72.24847 |
| 0.435 | 0.007135 | 60.96416 |
| 0.44 | 0.008554 | 51.43551 |
| 0.445 | 0.010256 | 43.39059 |
| 0.45 | 0.012295 | 36.59933 |
| 0.455 | 0.014741 | 30.86719 |
| 0.46 | 0.017672 | 26.02967 |
| 0.465 | 0.021187 | 21.9477 |
| 0.47 | 0.0254 | 18.50372 |
| 0.475 | 0.030452 | 15.59839 |
| 0.48 | 0.036508 | 13.14778 |
| 0.485 | 0.043769 | 11.08098 |
| 0.495 | 0.062909 | 7.868498 |
| 0.5 | 0.07542 | 6.629515 |
| 0.505 | 0.09042 | 5.585066 |
| 0.51 | 0.108402 | 4.704703 |
| 0.515 | 0.129961 | 3.962729 |
| 0.52 | 0.155807 | 3.337456 |
| 0.525 | 0.186794 | 2.810585 |
| 0.53 | 0.223943 | 2.366674 |
| 0.535 | 0.26848 | 1.992698 |
| 0.54 | 0.321875 | 1.67767 |
| 0.545 | 0.385889 | 1.412324 |
| 0.55 | 0.462633 | 1.188846 |
| 0.555 | 0.554641 | 1.000647 |
| 0.56 | 0.664947 | 0.842173 |
| 0.565 | 0.79719 | 0.70874 |
| 0.57 | 0.955733 | 0.596401 |
| 0.575 | 1.145807 | 0.50183 |
| 0.58 | 1.373682 | 0.422223 |
| 0.585 | 1.646877 | 0.355218 |
| 0.59 | 1.974404 | 0.298824 |
| 0.595 | 2.367069 | 0.251366 |
| 0.6 | 2.837827 | 0.211429 |
(b)
To draw: The graph for
(b)
Answer to Problem 46AP
The graph for
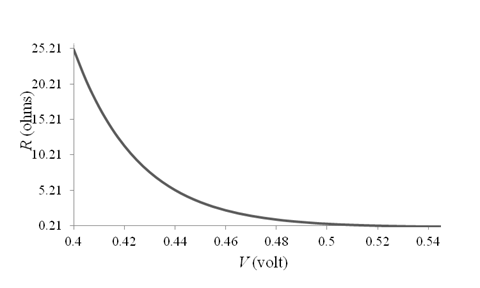
The graph for
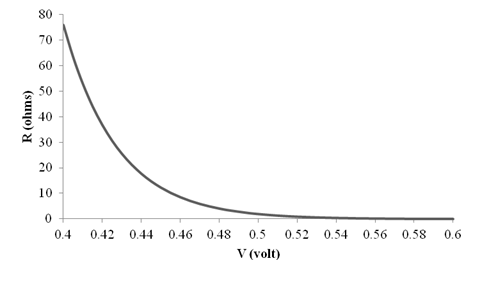
The graph for
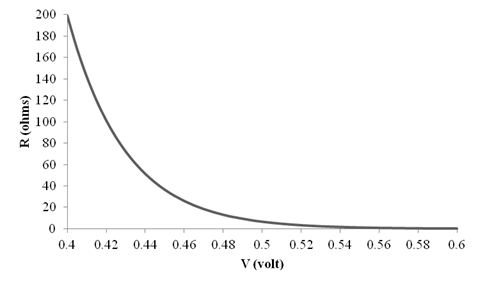
Explanation of Solution
Given information: The first symbol i.e. Euler’s number is
The different values of the
Thus, the graph for
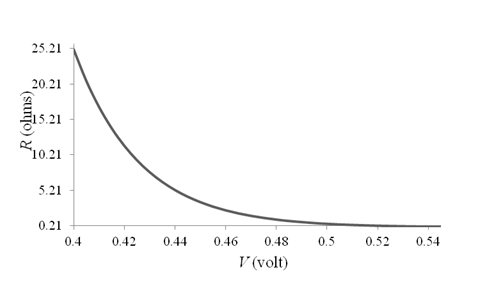
The different values of the
Thus, the graph for
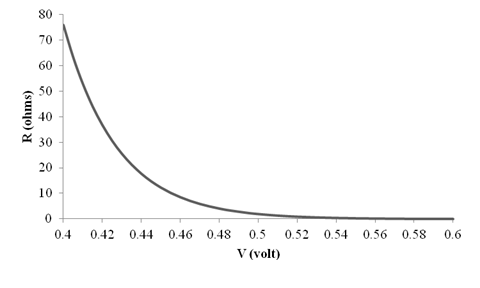
The different values of the
The graph for
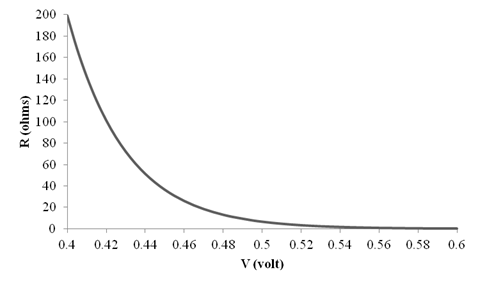
Conclusion:
Therefore, the graph for

Therefore, the graph for

Therefore, the graph for
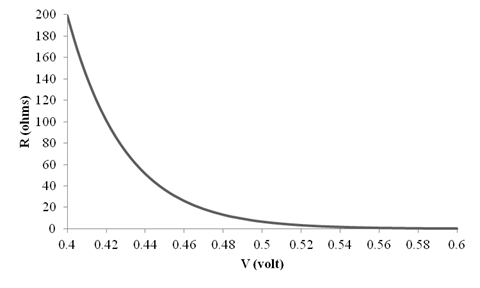
Want to see more full solutions like this?
Chapter 26 Solutions
Bundle: Physics For Scientists And Engineers With Modern Physics, Loose-leaf Version, 10th + Webassign Printed Access Card For Serway/jewett's Physics For Scientists And Engineers, 10th, Single-term
- 3.77 is not the correct answer!arrow_forwardA I squar frame has sides that measure 2.45m when it is at rest. What is the area of the frame when it moves parellel to one of its diagonal with a m² speed of 0.86.c as indicated in the figure? >V.arrow_forwardAn astronent travels to a distant star with a speed of 0.44C relative to Earth. From the austronaut's point of view, the star is 420 ly from Earth. On the return trip, the astronent travels speed of 0.76c relative to Earth. What is the distance covered on the return trip, as measured by the astronant? your answer in light-years. with a Give ly.arrow_forward
- star by spaceship Sixus is about 9.00 ly from Earth. To preach the star in 15.04 (ship time), how fast must you travel? C.arrow_forwardIf light-bulb A is unscrewed, how will the brightness of bulbs B and C change, if at all? How does the current drawn by from the battery change?arrow_forwardCan someone help mearrow_forward
- Can someone help me with this thank youarrow_forward(a) For a spherical capacitor with inner radius a and outer radius b, we have the following for the capacitance. ab C = k₂(b- a) 0.0695 m 0.145 m (8.99 × 10º N · m²/c²)( [0.145 m- 0.0695 m × 10-11 F = PF IIarrow_forwardA pendulum bob A (0.5 kg) is given an initialspeed of vA = 4 m/s when the chord ishorizontal. It then hits a stationary block B (1kg) which then slides to a maximum distanced before it stops. Determine the value of d.The coefficient of static friction between theblock and the plane is μk = 0.2. The coefficientof restitution between A and B is e = 0.8.Ans: d=1.0034 marrow_forward
- Figure 29-43 Problem 12. ••13 In Fig. 29-44, point P₁ is at distance R = 13.1 cm on the perpendicular bisector of a straight wire of length L = 18.0 cm carrying current i = 58.2 mA. (Note that the wire is not long.) What is the magnitude of the magnetic field at P₁ due to i? P2° R R Larrow_forwardCheckpoint 1 The figure shows the current i in a single-loop circuit with a battery B and a resistance R (and wires of neg- ligible resistance). (a) Should the emf arrow at B be drawn pointing leftward or rightward? At points a, B C R b, and c, rank (b) the magnitude of the current, (c) the electric potential, and (d) the electric potential energy of the charge carriers, greatest first.arrow_forwardPls help ASAParrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax





