
CALCULUS+ITS APPLICATIONS
15th Edition
ISBN: 9780137590612
Author: Goldstein
Publisher: RENT PEARS
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 2.6, Problem 2E
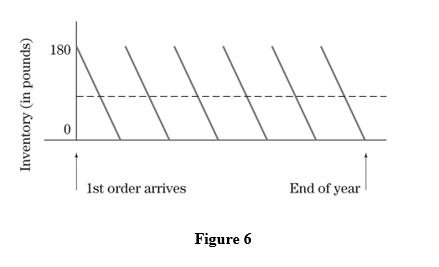
Refer to Fig. 6. Suppose that
The ordering cost for each delivery of dried cherries is
It costs
a. What is the inventory cost (carrying cost plus ordering cost) if carrying costs are computed on the average inventory during the order-reorder period?
b. What is the inventory cost if carrying costs are computed on the maximum inventory during the order-reorder period?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Can you answer this question and give step by step and why and how to get it. Can you write it (numerical method)
Can you answer this question and give step by step and why and how to get it. Can you write it (numerical method)
There are three options for investing $1150. The first earns 10% compounded annually, the second earns 10% compounded quarterly, and the third earns 10% compounded continuously. Find equations that model each investment growth and
use a graphing utility to graph each model in the same viewing window over a 20-year period. Use the graph to determine which investment yields the highest return after 20 years. What are the differences in earnings among the three
investment?
STEP 1: The formula for compound interest is
A =
nt
= P(1 + − − ) n²,
where n is the number of compoundings per year, t is the number of years, r is the interest rate, P is the principal, and A is the amount (balance) after t years. For continuous compounding, the formula reduces to
A = Pert
Find r and n for each model, and use these values to write A in terms of t for each case.
Annual Model
r=0.10
A = Y(t) = 1150 (1.10)*
n = 1
Quarterly Model
r = 0.10
n = 4
A = Q(t) = 1150(1.025) 4t
Continuous Model
r=0.10
A = C(t) =…
Chapter 2 Solutions
CALCULUS+ITS APPLICATIONS
Ch. 2.1 - Does the slope of the curve in Fig. 17 increases...Ch. 2.1 - At which labelled point on the graph in Fig. 18 is...Ch. 2.1 - Exercises 1-4 refer to graphs (a)-(f) in Fig.19...Ch. 2.1 - Exercises 1-4 refer to graphs (a)-(f) in Fig.19...Ch. 2.1 - Exercises 1-4 refer to graphs (a)-(f) in Fig.19...Ch. 2.1 - Exercises 1-4 refer to graphs (a)-(f) in Fig.19...Ch. 2.1 - Describe each of the following graphs. Your...Ch. 2.1 - Describe each of the following graphs. Your...Ch. 2.1 - Describe each of the following graphs. Your...Ch. 2.1 - Describe each of the following graphs. Your...
Ch. 2.1 - Describe each of the following graphs. Your...Ch. 2.1 - Prob. 10ECh. 2.1 - Describe each of the following graphs. Your...Ch. 2.1 - Prob. 12ECh. 2.1 - Describe the way the slope changes as you move...Ch. 2.1 - Prob. 14ECh. 2.1 - Describe the way the slope changes on the graph in...Ch. 2.1 - Prob. 16ECh. 2.1 - Exercise 17 and 18 refer to the graph in Fig 20....Ch. 2.1 - Exercise 17 and 18 refer to the graph in Fig 20....Ch. 2.1 - Prob. 19ECh. 2.1 - In Exercises 19-22, draw the graph of a function...Ch. 2.1 - In Exercises 19-22, draw the graph of a function...Ch. 2.1 - Prob. 22ECh. 2.1 - Prob. 23ECh. 2.1 - Prob. 24ECh. 2.1 - A Patients Temperature At noon, a childs...Ch. 2.1 - Prob. 26ECh. 2.1 - Blood Flow through the Brain One method of...Ch. 2.1 - Pollution Suppose that some organic waste products...Ch. 2.1 - Prob. 29ECh. 2.1 - Prob. 30ECh. 2.1 - Prob. 31ECh. 2.1 - Let P(t) be the population of a bacteria culture...Ch. 2.1 - In Exercises 3336, sketch the graph of a function...Ch. 2.1 - In Exercises 3336, sketch the graph of a function...Ch. 2.1 - In Exercises 3336, sketch the graph of a function...Ch. 2.1 - In Exercises 3336, sketch the graph of a function...Ch. 2.1 - Consider a smooth curve with no undefined points....Ch. 2.1 - If the function f(x) has a relative minimum at x=a...Ch. 2.1 - Technology Exercises Graph the function...Ch. 2.1 - Prob. 40ECh. 2.1 - Technology Exercises Simultaneously graph the...Ch. 2.2 - Make a good sketch of the function f(x) near the...Ch. 2.2 - The graph of f(x)=x3 is shown in Fig. 15. Is the...Ch. 2.2 - The graph of y=f(x) is shown in Fig. 16. Explain...Ch. 2.2 - Exercises 14 refer to the functions whose graphs...Ch. 2.2 - Exercises 14 refer to the functions whose graphs...Ch. 2.2 - Exercises 14 refer to the functions whose graphs...Ch. 2.2 - Exercises 14 refer to the functions whose graphs...Ch. 2.2 - Which one of the graph in Fig. 18 could represent...Ch. 2.2 - Which one of the graphs in Fig. 18 could represent...Ch. 2.2 - In Exercises 712, sketch the graph of a function...Ch. 2.2 - In Exercises 712, sketch the graph of a function...Ch. 2.2 - In Exercises 712, sketch the graph of a function...Ch. 2.2 - In Exercises 712, sketch the graph of a function...Ch. 2.2 - In Exercises 712, sketch the graph of a function...Ch. 2.2 - In Exercises 712, sketch the graph of a function...Ch. 2.2 - In Exercises 1318, use the given information to...Ch. 2.2 - In Exercises 1318, use the given information to...Ch. 2.2 - In Exercises 1318, use the given information to...Ch. 2.2 - In Exercises 1318, use the given information to...Ch. 2.2 - In Exercises 1318, use the given information to...Ch. 2.2 - In Exercises 1318, use the given information to...Ch. 2.2 - Refer to the graph in Fig. 19. Fill in each box of...Ch. 2.2 - The first and second derivatives of the function...Ch. 2.2 - Suppose that Fig. 20 contains the graph of y=s(t),...Ch. 2.2 - Suppose that Fig. 20 contains the graph of y=v(t),...Ch. 2.2 - 23. Refer to figure 21, Looking at the graph f(x),...Ch. 2.2 - In figure 22, the t axis represent the time in...Ch. 2.2 - 25. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - 26. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - 27. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - 28. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - 29. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - 30. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - 31. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - Prob. 32ECh. 2.2 - 33. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - 34. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - 35. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - Prob. 36ECh. 2.2 - 37. Level of Water from Melting Snow Melting snow...Ch. 2.2 - 38. Changes in Temperature T(t) is the temperature...Ch. 2.2 - Prob. 39ECh. 2.2 - Prob. 40ECh. 2.2 - Prob. 41ECh. 2.2 - 42. Match each observation (a)(e) with a...Ch. 2.2 - Prob. 43ECh. 2.2 - Drug Diffusion in the Bloodstream After a drug is...Ch. 2.2 - Prob. 45ECh. 2.2 - Prob. 46ECh. 2.3 - Which of the curves in Fig.15 could possibly be...Ch. 2.3 - Which of the curves in Fig.16 could be the graph...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Prob. 14ECh. 2.3 - Prob. 15ECh. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Prob. 24ECh. 2.3 - Sketch the following curves, indicating all...Ch. 2.3 - Sketch the following curves, indicating all...Ch. 2.3 - Sketch the following curves, indicating all...Ch. 2.3 - Sketch the following curves, indicating all...Ch. 2.3 - Sketch the following curves, indicating all...Ch. 2.3 - Sketch the following curves, indicating all...Ch. 2.3 - Prob. 31ECh. 2.3 - Prob. 32ECh. 2.3 - Prob. 33ECh. 2.3 - Let a,b,c,d be fixed numbers with a0, and let...Ch. 2.3 - The graph of each function in Exercises 35 40 has...Ch. 2.3 - Prob. 36ECh. 2.3 - The graph of each function in Exercises 35 40 has...Ch. 2.3 - The graph of each function in Exercises 35 40 has...Ch. 2.3 - The graph of each function in Exercises 35 40 has...Ch. 2.3 - The graph of each function in Exercises 35 40 has...Ch. 2.3 - In Exercises 41 and 42, determine which function...Ch. 2.3 - In Exercises 41 and 42, determine which function...Ch. 2.3 - Consider the graph of g(x) in Fig. 17. a. If g(x)...Ch. 2.3 - U. S. Population The population (in millions) of...Ch. 2.3 - Index-Fund Fees When a mutual fund company charges...Ch. 2.3 - Prob. 46ECh. 2.3 - Technology Exercises Draw the graph of...Ch. 2.3 - Technology Exercises Draw the graph of...Ch. 2.3 - Technology Exercises Draw the graph of...Ch. 2.3 - Technology Exercises Draw the graph of...Ch. 2.4 - Determine whether each of the following functions...Ch. 2.4 - Prob. 2CYUCh. 2.4 - Prob. 3CYUCh. 2.4 - Find the x intercepts of the given function....Ch. 2.4 - Prob. 2ECh. 2.4 - Find the x intercepts of the given function....Ch. 2.4 - Prob. 4ECh. 2.4 - Find the x intercepts of the given function....Ch. 2.4 - Find the x intercepts of the given function....Ch. 2.4 - Show that the function f(x)=13x32x2+5x has no...Ch. 2.4 - Prob. 8ECh. 2.4 - Sketch the graphs of the following functions....Ch. 2.4 - Sketch the graphs of the following functions....Ch. 2.4 - Sketch the graphs of the following functions....Ch. 2.4 - Sketch the graphs of the following functions....Ch. 2.4 - Sketch the graphs of the following functions....Ch. 2.4 - Prob. 14ECh. 2.4 - Sketch the graphs of the following functions....Ch. 2.4 - Prob. 16ECh. 2.4 - Sketch the graphs of the following functions....Ch. 2.4 - Prob. 18ECh. 2.4 - Sketch the graphs of the following functions....Ch. 2.4 - Sketch the graphs of the following functions....Ch. 2.4 - Prob. 21ECh. 2.4 - Prob. 22ECh. 2.4 - Sketch the graphs of the following functions for...Ch. 2.4 - Prob. 24ECh. 2.4 - Sketch the graphs of the following functions for...Ch. 2.4 - Prob. 26ECh. 2.4 - Sketch the graphs of the following functions for...Ch. 2.4 - Prob. 28ECh. 2.4 - Prob. 29ECh. 2.4 - Prob. 30ECh. 2.4 - Prob. 31ECh. 2.4 - Prob. 32ECh. 2.4 - Find the quadratic function f(x)=ax2+bx+c that...Ch. 2.4 - Prob. 34ECh. 2.4 - Prob. 35ECh. 2.4 - Prob. 36ECh. 2.4 - Prob. 37ECh. 2.4 - Technology Exercises Height of Tropical Grass The...Ch. 2.5 - Volume A canvas wind shelter for the beach has a...Ch. 2.5 - Prob. 2CYUCh. 2.5 - For what x does the function g(x)=10+40xx2 have...Ch. 2.5 - Find the maximum value of the function f(x)=12xx2,...Ch. 2.5 - Find the minimum value of f(t)=t36t2+40, t0 and...Ch. 2.5 - For what t does the function f(t)=t2-24t have its...Ch. 2.5 - Optimization with Constraint Find the maximum of...Ch. 2.5 - Optimization with Constraint Find two positive...Ch. 2.5 - Optimization with Constraint Find the minimum of...Ch. 2.5 - In Exercise 7, can there be a maximum for Q=x2+y2...Ch. 2.5 - Minimizing a Sum Find the positive values of x and...Ch. 2.5 - Maximizing a Product Find the positive values of...Ch. 2.5 - Area There are 320 available to fence in a...Ch. 2.5 - Volume Figure 12 (b) shows an open rectangular box...Ch. 2.5 - Volume Postal requirements specify that parcels...Ch. 2.5 - Perimeter Consider the problem of finding the...Ch. 2.5 - Cost A rectangular garden of area 75 square feet...Ch. 2.5 - Cost A closed rectangular box with a square base...Ch. 2.5 - Surface Area Find the dimensions of the closed...Ch. 2.5 - Volume A canvas wind shelter for the beach has a...Ch. 2.5 - Area A farmer has 1500 available to build an...Ch. 2.5 - Area Find the dimensions of the rectangular garden...Ch. 2.5 - Maximizing a Product Find two positive numbers,...Ch. 2.5 - Minimizing a Sum Find two positive numbers, xandy,...Ch. 2.5 - Area Figure 140 (a) shows a Norman window, which...Ch. 2.5 - Surface Area A large soup can is to be designed so...Ch. 2.5 - In Example 3 we can solve the constraint equation...Ch. 2.5 - Cost A ship uses 5x2 dollars of fuel per hour when...Ch. 2.5 - Cost A cable is to be installed from one corner,...Ch. 2.5 - Area A rectangular page is to contain 50 square...Ch. 2.5 - Distance Find the point on the graph of y=x that...Ch. 2.5 - Prob. 30ECh. 2.5 - Distance Find the point on the line y=2x+5 that is...Ch. 2.5 - Technology Exercise Inscribed Rectangle of Maximum...Ch. 2.6 - In the inventory problem of Example 2, suppose...Ch. 2.6 - In the inventory problem Example 2, Suppose that...Ch. 2.6 - Inventory Problem Figure 6 shows the inventory...Ch. 2.6 - Refer to Fig. 6. Suppose that The ordering cost...Ch. 2.6 - Inventory Control A pharmacist wants to establish...Ch. 2.6 - Inventory Control A furniture store expects to...Ch. 2.6 - Inventory Control A California distributor of...Ch. 2.6 - Economic Lot Size The Great American Tire Co....Ch. 2.6 - Prob. 7ECh. 2.6 - Prob. 8ECh. 2.6 - Prob. 9ECh. 2.6 - Prob. 10ECh. 2.6 - Area Starting with a 100-foot-long stone wall, a...Ch. 2.6 - Prob. 12ECh. 2.6 - Length A rectangular corral of 54 square meters is...Ch. 2.6 - Refer to Exercise 13. If the cost of the fencing...Ch. 2.6 - Revenue Shakespeares Pizza sells 1000 large vegi...Ch. 2.6 - Prob. 16ECh. 2.6 - Cost A storage shed is to be built in the shape of...Ch. 2.6 - Cost A supermarket is to be designed as a...Ch. 2.6 - Volume A certain airline requires that rectangular...Ch. 2.6 - Area An athletic field [Fig.8] consists of a...Ch. 2.6 - Volume An open rectangular box is to be...Ch. 2.6 - Volume A closed rectangular box is to be...Ch. 2.6 - Amount of Oxygen in a Lake Let f(t) be the amount...Ch. 2.6 - Prob. 24ECh. 2.6 - Area Consider a parabolic arch whose shape may be...Ch. 2.6 - Prob. 26ECh. 2.6 - Surface Area An open rectangular box of volume 400...Ch. 2.6 - If f(x) is defined on the interval 0x5 and f(x) is...Ch. 2.6 - Technology Exercises Volume A pizza box is formed...Ch. 2.6 - Technology Exercises Consumption of Coffee in the...Ch. 2.7 - Prob. 1CYUCh. 2.7 - Rework Example 4 under the condition that the...Ch. 2.7 - On a certain route, a regional airline carries...Ch. 2.7 - Minimizing Marginal Cost Given the cost function...Ch. 2.7 - Minimizing Marginal Cost If a total cost function...Ch. 2.7 - Maximizing Revenue Cost The revenue function for a...Ch. 2.7 - Maximizing Revenue The revenue function for a...Ch. 2.7 - Cost and Profit A one-product firm estimates that...Ch. 2.7 - Maximizing Profit A small tie shop sells ties for...Ch. 2.7 - Demand and Revenue The demand equation for a...Ch. 2.7 - Maximizing Revenue The demand equation for a...Ch. 2.7 - Profit Some years ago, it was estimated that the...Ch. 2.7 - Maximizing Area Consider a rectangle in the xy-...Ch. 2.7 - Demand, Revenue, and Profit Until recently...Ch. 2.7 - Demand and Revenue The average ticket price for a...Ch. 2.7 - Demand and Revenue An artist is planning to sell...Ch. 2.7 - Demand and Revenue A swimming club offers...Ch. 2.7 - Prob. 15ECh. 2.7 - Prob. 16ECh. 2.7 - Price Setting The monthly demand equation for an...Ch. 2.7 - Taxes, Profit, and Revenue The demand equation for...Ch. 2.7 - Interest Rate A savings and loan association...Ch. 2.7 - Prob. 20ECh. 2.7 - Revenue The revenue for a manufacturer is R(x)...Ch. 2.7 - Prob. 22ECh. 2 - State as many terms used to describe graphs of...Ch. 2 - What is the difference between having a relative...Ch. 2 - Give three characterizations of what it means for...Ch. 2 - What does it mean to say that the graph of f(x)...Ch. 2 - Prob. 5FCCECh. 2 - Prob. 6FCCECh. 2 - Prob. 7FCCECh. 2 - Prob. 8FCCECh. 2 - Prob. 9FCCECh. 2 - Prob. 10FCCECh. 2 - Prob. 11FCCECh. 2 - Prob. 12FCCECh. 2 - Prob. 13FCCECh. 2 - Prob. 14FCCECh. 2 - Outline the procedure for solving an optimization...Ch. 2 - Prob. 16FCCECh. 2 - Figure (1) contains the graph of f(x), the...Ch. 2 - Figure (2) shows the graph of function f(x) and...Ch. 2 - In Exercise 36, draw the graph of a function f(x)...Ch. 2 - In Exercise 36, draw the graph of a function f(x)...Ch. 2 - In Exercise 36, draw the graph of a function f(x)...Ch. 2 - In Exercise 36, draw the graph of a function f(x)...Ch. 2 - Exercise 712, refer to the graph in Fig. 3. List...Ch. 2 - Exercise 712, refer to the graph in Fig. 3. List...Ch. 2 - Exercise 712, refer to the graph in Fig. 3. List...Ch. 2 - Exercise 712, refer to the graph in Fig. 3. List...Ch. 2 - Exercise 712, refer to the graph in Fig. 3. List...Ch. 2 - Exercise 712, refer to the graph in Fig. 3. List...Ch. 2 - Properties of various functions are described...Ch. 2 - Properties of various functions are described...Ch. 2 - Properties of various functions are described...Ch. 2 - Properties of various functions are described...Ch. 2 - Properties of various functions are described...Ch. 2 - Properties of various functions are described...Ch. 2 - Properties of various functions are described...Ch. 2 - Prob. 20RECh. 2 - In Fig. 4 (a) and 4 (b), the t axis represents...Ch. 2 - U.S. Electric Energy United States electrical...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following curves. y=2x3+3x2+1Ch. 2 - Sketch the following curves. y=x332x26xCh. 2 - Sketch the following curves. y=x33x2+3x2Ch. 2 - Sketch the following curves. y=100+36x6x2x3Ch. 2 - Sketch the following curves. y=113+3xx213x3Ch. 2 - Sketch the following curves. y=x33x29x+7Ch. 2 - Sketch the following curves. y=13x32x25xCh. 2 - Sketch the following curves. y=x36x215x+50Ch. 2 - Sketch the following curves. y=x42x2Ch. 2 - Sketch the following curves. y=x44x3Ch. 2 - Sketch the following curves. y=x5+20x+3(x0)Ch. 2 - Sketch the following curves. y=12x+2x+1(x0)Ch. 2 - Let f(x)=(x2+2)3/2. Show that the graph of f(x)...Ch. 2 - Show that the function f(x)=(2x2+3)3/2 is...Ch. 2 - Let f(x) be a function whose derivative is...Ch. 2 - Let f(x) be a function whose derivative is...Ch. 2 - Position Velocity and Acceleration A car traveling...Ch. 2 - The water level in a reservoir varies during the...Ch. 2 - Population near New York City Let f(x) be the...Ch. 2 - For what x does the function f(x)=14x2x+2,0x8,...Ch. 2 - Find the maximum value of the function...Ch. 2 - Find the minimum value of the function...Ch. 2 - Surface Area An open rectangular box is to be 4...Ch. 2 - Volume A closed rectangular box with a square base...Ch. 2 - Volume A long rectangular sheet of metal 30 inches...Ch. 2 - Maximizing the Total Yield A small orchard yields...Ch. 2 - Inventory Control A publishing company sells...Ch. 2 - Profit if the demand equation for a monopolist is...Ch. 2 - Minimizing time Jane wants to drive her tractor...Ch. 2 - Maximizing Revenue A travel agency offers a boat...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Use a graphing utility to find the point of intersection, if any, of the graphs of the functions. Round your result to three decimal places. (Enter NONE in any unused answer blanks.) y = 100e0.01x (x, y) = y = 11,250 ×arrow_forward5. For the function y-x³-3x²-1, use derivatives to: (a) determine the intervals of increase and decrease. (b) determine the local (relative) maxima and minima. (e) determine the intervals of concavity. (d) determine the points of inflection. (e) sketch the graph with the above information indicated on the graph.arrow_forwardCan you solve this 2 question numerical methodarrow_forward
- 1. Estimate the area under the graph of f(x)-25-x from x=0 to x=5 using 5 approximating rectangles Using: (A) right endpoints. (B) left endpoints.arrow_forward9. Use fundamental theorem of calculus to find the derivative d a) *dt sin(x) b)(x)√1-2 dtarrow_forward3. Evaluate the definite integral: a) √66x²+8dx b) x dx c) f*(2e* - 2)dx d) √√9-x² e) (2-5x)dx f) cos(x)dx 8)²₁₂√4-x2 h) f7dx i) f² 6xdx j) ²₂(4x+3)dxarrow_forward
- 2. Consider the integral √(2x+1)dx (a) Find the Riemann sum for this integral using right endpoints and n-4. (b) Find the Riemann sum for this same integral, using left endpoints and n=4arrow_forwardProblem 11 (a) A tank is discharging water through an orifice at a depth of T meter below the surface of the water whose area is A m². The following are the values of a for the corresponding values of A: A 1.257 1.390 x 1.50 1.65 1.520 1.650 1.809 1.962 2.123 2.295 2.462|2.650 1.80 1.95 2.10 2.25 2.40 2.55 2.70 2.85 Using the formula -3.0 (0.018)T = dx. calculate T, the time in seconds for the level of the water to drop from 3.0 m to 1.5 m above the orifice. (b) The velocity of a train which starts from rest is given by the fol- lowing table, the time being reckoned in minutes from the start and the speed in km/hour: | † (minutes) |2|4 6 8 10 12 14 16 18 20 v (km/hr) 16 28.8 40 46.4 51.2 32.0 17.6 8 3.2 0 Estimate approximately the total distance ran in 20 minutes.arrow_forwardX Solve numerically: = 0,95 In xarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you


 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning



College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Use of ALGEBRA in REAL LIFE; Author: Fast and Easy Maths !;https://www.youtube.com/watch?v=9_PbWFpvkDc;License: Standard YouTube License, CC-BY
Compound Interest Formula Explained, Investment, Monthly & Continuously, Word Problems, Algebra; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=P182Abv3fOk;License: Standard YouTube License, CC-BY
Applications of Algebra (Digit, Age, Work, Clock, Mixture and Rate Problems); Author: EngineerProf PH;https://www.youtube.com/watch?v=Y8aJ_wYCS2g;License: Standard YouTube License, CC-BY