Chapter 25, Problem 25.13CRE

(a)

To determine

To plot the data and obtain the equation of the least squares regression line expressing width as a fraction of length.

Answer to Problem 25.13CRE

The regression equation is:

  $\text{<mover accent="true"><mo>W</mo><mo>^</mo></mover> idth}=-0.6487+0.1822\times \text{Length}$ .

Explanation of Solution

In the question we have given the data in a table on the size of perch in a lake in Finland. Here we have to examine the relationship between width (y) and length (x) in perch. Thus, we have selected the data of the table and using excel we have constructed a scatter plot by clicking on the insert option and then going to the chart option tab and then selecting scatter plot. Then by going to the quick layout option we selected the graph with function option and then the scatterplot is as follows:

  

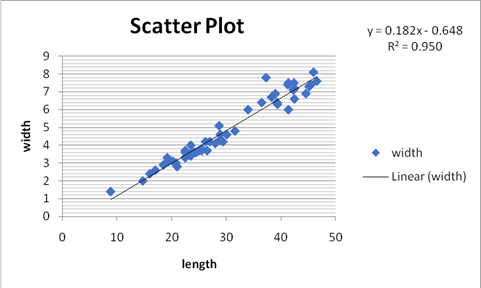
Here the length is on the horizontal line and width is on the vertical line. Thus, from this we can say that the relationship between width (y) and length (x) in perch is linear as the points are near to each other and positive in nature as they are moving in upward direction. Also, from the scatterplot, the equation of the least squares regression line expressing width as a fraction of length is as:

  $\begin{array}{l}\widehat{y}=a+bx\\ \Rightarrow \text{<mover accent="true"><mo>W</mo><mo>^</mo></mover> idth}=-0.6487+0.1822\times \text{Length}\end{array}$

(b)

To determine

To find out how well can we predict the width of a perch from its length.

Explanation of Solution

In the question we have given the data in a table on the size of perch in a lake in Finland. Here we have to examine the relationship between width (y) and length (x) in perch. And, the equation of the least squares regression line expressing width as a fraction of length is as:

  $\begin{array}{l}\widehat{y}=a+bx\\ \Rightarrow \text{<mover accent="true"><mo>W</mo><mo>^</mo></mover> idth}=-0.6487+0.1822\times \text{Length}\end{array}$

Since the $R^2=0.9508$ , which is near to one. Therefore, the coefficient of determination is near to one so it will be the good prediction of the width of a perch from its length. Since there relation is very strong and close to one.

(c)

To determine

To predict the mean width of such fish and give a $95\%$ confidence interval.

Answer to Problem 25.13CRE

The mean of the width of fish is $4.271$ and the confidence interval is $(0.1709,0.1935)$ .

Explanation of Solution

In the question we have given the data in a table on the size of perch in a lake in Finland. Here we have to examine the relationship between width (y) and length (x) in perch. And, the equation of the least squares regression line expressing width as a fraction of length is as:

  $\begin{array}{l}\widehat{y}=a+bx\\ \Rightarrow \text{<mover accent="true"><mo>W</mo><mo>^</mo></mover> idth}=-0.6487+0.1822\times \text{Length}\end{array}$

It is given that the length of a typical perch is about $x*=27$ cm. Then the width of such perch will be:

  $\begin{array}{l}\text{<mover accent="true"><mo>W</mo><mo>^</mo></mover> idth}=-0.6487+0.1822\times \text{Length}\\ =-0.6487+0.1822\times 27\\ =4.271\end{array}$

And the $95\%$ confidence interval is calculated by using excel. First go to the data tab and select the data analysis option. The dialogue box will appear and then select the regression from it click OK. Then another dialogue box will appear in which insert the data values and select the confidence interval. Then the confidence interval will appear as:

	Coefficients	Standard Error	t Stat	P-value	Lower 95%	Upper 95%
Intercept	-0.648744077	0.175139507	-3.704156116	0.000500034	-0.999877647	-0.297610506
length	0.182225914	0.005642218	32.29685578	5.40028E-37	0.170913947	0.193537881

Thus, the confidence interval is:

  $(0.1709,0.1935)$ .

(d)

To determine

To examine the residual and explain does fish number $\text{143}$ have an unusually large residual and how might this impact inference.

Answer to Problem 25.13CRE

Yes, the fish number $\text{143}$ have an unusually large residual.

Explanation of Solution

In the question we have given the data in a table on the size of perch in a lake in Finland. Here we have to examine the relationship between width (y) and length (x) in perch. And, the equation of the least squares regression line expressing width as a fraction of length is as:

  $\begin{array}{l}\widehat{y}=a+bx\\ \Rightarrow \text{<mover accent="true"><mo>W</mo><mo>^</mo></mover> idth}=-0.6487+0.1822\times \text{Length}\end{array}$

For analyzing the residual, we will use excel. First go to the data tab and select the data analysis option. The dialogue box will appear and then select the regression from it click OK. Then another dialogue box will appear in which insert the data values and then the regression plot will appear as:

  

We can see from the residual plot that the points are near to each other but at the end they are more scattered and from this we can we that the fish number $\text{143}$ is very wide for its length and therefore it appears unusually large residual than the other points and it can make inference very less accurate.