
Concept explainers
Solve the following initial value problem over the interval from
(a) Analytically.
(b) Euler's method with
(c) Midpoint method with
(d) Fourth-order RK method with
(a)
To calculate: The solution of the initial value problem
Answer to Problem 1P
Solution:
The solution to the initial value problem is
Explanation of Solution
Given Information:
The initial value problem
Formula used:
Tosolve an initial value problem of the form
Calculation:
Rewrite the provided differential equation as,
Integrate both sides to get,
Now use the initial condition
Hence, the analytical solution of the initial value problem is
(b)
To calculate: The solution of the initial value problem
Answer to Problem 1P
Solution:
For
| t | y | |
| 0 | 1 | |
| 0.5 | 0.45 | |
| 1 | 0.25875 | |
| 1.5 | 0.245813 | 0.282684 |
| 2 | 0.387155 | 1.122749 |
And, for
| t | y | |
| 0 | 1 | |
| 0.25 | 0.725 | |
| 0.5 | 0.536593 | |
| 0.75 | 0.422861 | |
| 1 | 0.36603 | |
| 1.25 | 0.356879 | 0.165057 |
| 1.5 | 0.398143 | 0.457865 |
| 1.75 | 0.51261 | 1.005997 |
| 2 | 0.764109 | 2.215916 |
Explanation of Solution
Given Information:
The initial value problem
Formula used:
Solve an initial value problem of the form
Calculation:
From the initial condition
Let
Proceed further and use the following MATLAB code to implement Euler’s method and solve the differential equation.
Execute the above code to obtain the solutions for
| t | y | |
| 0 | 1 | |
| 0.5 | 0.45 | |
| 1 | 0.25875 | |
| 1.5 | 0.245813 | 0.282684 |
| 2 | 0.387155 | 1.122749 |
Now, the similar procedure can be followedfor the step size
The results thus obtained are tabulated as,
| t | y | |
| 0 | 1 | |
| 0.25 | 0.725 | |
| 0.5 | 0.536593 | |
| 0.75 | 0.422861 | |
| 1 | 0.36603 | |
| 1.25 | 0.356879 | 0.165057 |
| 1.5 | 0.398143 | 0.457865 |
| 1.75 | 0.51261 | 1.005997 |
| 2 | 0.764109 | 2.215916 |
The results for the two-step-sizes are plotted along with the analytical solution
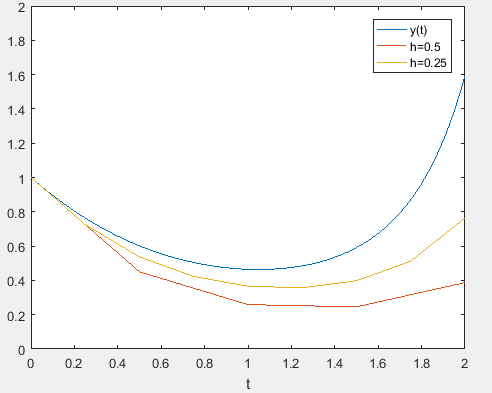
It is inferred that the smaller step-size would give a better approximation to the solution.
(c)
To calculate: The solution of the initial value problem
Answer to Problem 1P
Solution:
The solutions are tabulated as,
| t | y | |
| 0 | 1 | |
| 0.5 | 0.623906 | |
| 1 | 0.491862 | |
| 1.5 | 0.602762 | 0.693176 |
| 2 | 1.364267 | 3.956374 |
Explanation of Solution
Given Information:
The initial value problem
Formula used:
Solve an initial value problem of the form
Here,
Calculation:
From the initial condition
Let
Now,
Proceed further and use the following MATLAB code to implement mid-point iterative scheme and solve the differential equation.
Execute the above code to obtain the solutions tabulated as,
| t | Y | |
| 0 | 1 | |
| 0.5 | 0.623906 | |
| 1 | 0.491862 | |
| 1.5 | 0.602762 | 0.693176 |
| 2 | 1.364267 | 3.956374 |
The results for the are plotted along with the analytical solution
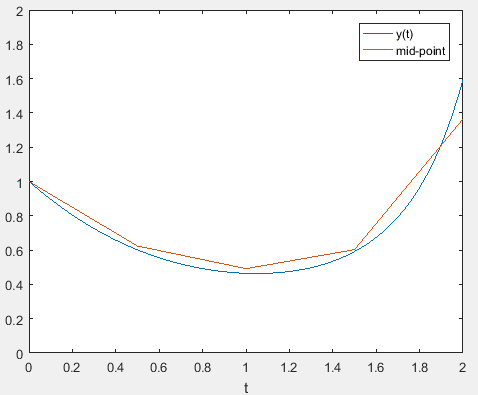
Thus, it is inferred that the mid-point method gives a good approximation to the solution.
(d)
To calculate: The solution of the initial value problem
Answer to Problem 1P
Solution:
The solutions are tabulated as,
| t | y | ||||
| 0 | 1 | ||||
| 0.5 | 0.6016 | ||||
| 1 | 0.4645 | 0.2095 | 0.2391 | 0.6717 | |
| 1.5 | 0.5914 | 0.6801 | 1.4953 | 1.8937 | 4.4609 |
| 2 | 1.5845 | 4.5949 | 10.8302 | 17.0071 | 51.9532 |
Explanation of Solution
Given Information:
The initial value problem
Formula used:
Solve an initial value problem of the form
In the above expression,
Calculation:
From the initial condition
Let
And,
And,
Therefore,
Proceed further and use the following MATLAB code to implement RK method of order four, solve the differential equation.
In an another .m file, define the equation as,
Execute the above code to obtain the solutions tabulated as,
| t | y | ||||
| 0 | 1 | ||||
| 0.5 | 0.6016 | ||||
| 1 | 0.4645 | 0.2095 | 0.2391 | 0.6717 | |
| 1.5 | 0.5914 | 0.6801 | 1.4953 | 1.8937 | 4.4609 |
| 2 | 1.5845 | 4.5949 | 10.8302 | 17.0071 | 51.9532 |
The results for the are plotted along with the analytical solution
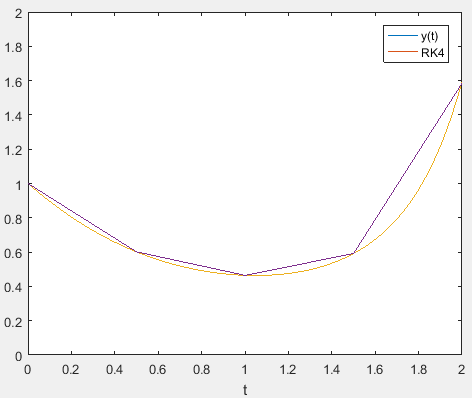
Hence, it is inferred that the RK method of order four gives the best approximation to the solution.
Want to see more full solutions like this?
Chapter 25 Solutions
Numerical Methods for Engineers
- [Q2]: The cost information supplied by the cost accountant is as follows:Sales 20,00 units, $ 10 per unitCalculate the (a/ newsale guantity and (b) new selling price to earn the sameVariable cost $ 6 per unit, Fixed Cost $ 30,000, Profit $ 50,000profit ifi) Variable cost increases by $ 2 per unitil) Fixed cost increase by $ 10,000Ili) Variable cost increase by $ 1 per unit and fixed cost reduces by $ 10,000arrow_forwardcan you please help me perform Visual Inspection and Fractography of the attatched image: Preliminary examination to identify the fracture origin, suspected fatigue striation, and corrosion evidences.arrow_forwardcan you please help[ me conduct Causal Analysis (FTA) on the scenario attatched: FTA diagram which is a fault tree analysis diagram will be used to gain an overview of the entire path of failure from root cause to the top event (i.e., the swing’s detachment) and to identify interactions between misuse, material decay and inspection errors.arrow_forward
- hi can you please help me in finding the stress intensity factor using a k-calcluator for the scenario attathced in the images.arrow_forwardHi, can you please help me .Identify and justify suitable analytical techniques of the scenario below, bearing in mind the kinds of information being handled to reach a conclusion (methodology). A child swing set was discovered to have failed at the fixing at the top of the chains connecting the seat to the top of the swing set. A 12 mm threaded steel bolt, connecting the shackle to the top beam, failed at the start of the threaded region on the linkage closest to the outside side of the swing set . The linkage and bolts were made of electro galvanised mild steel . The rigid bar chain alternatives and fixings were of the same material and appeared to be fitted in accordance with guidelines. The yield strength of the steel used is 260 MPa and the UTS is 380 MPa. The bolt that failed was threaded using a standard thread with a pitch (distance between threads) of 1.75 mm and a depth of approximately 1.1 mm. The swing set in question had been assigned to ‘toddlers’ with the application of…arrow_forwardHi, can you please define and calculate the failure mode of the linkage that failed on the swing (images added) : A child swing set was discovered to have failed at the fixing at the top of the chains connecting the seat to the top of the swing set. A 12 mm threaded steel bolt, connecting the shackle to the top beam, failed at the start of the threaded region on the linkage closest to the outside side of the swing set . The linkage and bolts were made of electro galvanised mild steel . The rigid bar chain alternatives and fixings were of the same material and appeared to be fitted in accordance with guidelines. The yield strength of the steel used is 260 MPa and the UTS is 380 MPa. The bolt that failed was threaded using a standard thread with a pitch (distance between threads) of 1.75 mm and a depth of approximately 1.1 mm. The swing set in question had been assigned to ‘toddlers’ with the application of a caged-type seat. However, the location was within the play area not…arrow_forward
- Page 11-68. The rectangular plate shown is subjected to a uniaxial stress of 2000 psi. Compute the shear stress and the tensile developed on a plane forming an angle of 30° with the longitud axis of the member. (Hint: Assume a cross-sectional area of unity) 2000 psi 2000 psi hparrow_forward11-70. A shear stress (pure shear) of 5000 psi exists on an element. (a) Determine the maximum tensile and compressive stresses caused in the element due to this shear. (b) Sketch the element showing the planes on which the maximum tensile and compressive stresses act.arrow_forward11-20. An aluminum specimen of circular cross section, 0.50 in. in diameter, ruptured under a tensile load of 12,000 lb. The plane of failure was found to be at 48° with a plane perpendicular to the longitudinal axis of the specimen. (a) Compute the shear stress on the failure plane. (b) Compute the maximum tensile stress. (c) Compute the tensile stress on the failure plane. hparrow_forward
- A long flat steel bar 13 mm thick and 120 mm wide has semicircular grooves as shown and carries a tensile load of 50 kN Determine the maximum stress if plate r= 8mm r=21mm r=38mmarrow_forwardProblem 13: F₁ = A =250 N 30% Determine the moment of each of the three forces about point B. F₂ = 300 N 60° 2 m -3 m B 4 m F3=500 Narrow_forward3 kN 3 kN 1.8 kN/m 80 mm B 300 mm D an 1.5 m-1.5 m--1.5 m- PROBLEM 5.47 Using the method of Sec. 5.2, solve Prob. 5.16 PROBLEM 5.16 For the beam and loading shown, determine the maximum normal stress due to bending on a transverse section at C.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





