
Concept explainers
a.
Identify the null hypothesis and alternative hypothesis.
a.
Answer to Problem 1E
Null hypothesis:
Alternative hypothesis:
Explanation of Solution
The given information is that, a student conducted an experiment to identify whether there is any significant difference in the four popcorn brands. The number of kernels which was left unpopped, were also recorded. The student measured pops of each brand four times. The F-ratio obtained from the test is 13.56.
Let
The null hypothesis is framed by assuming that all the four brands of popcorn results in the same mean number of unpopped kernels.
Null hypothesis:
The mean number of unpopped kernels obtained from each of the four brands of popcorn is the same.
Alternative hypothesis:
The mean number of unpopped kernels obtained at least one of the brand is different from the rest of the brands.
b.
Find the degrees of freedom for the treatment sum of squares and the error sum of squares.
b.
Answer to Problem 1E
The degrees of freedom for the treatment sum of squares is 3.
The degrees of freedom for the error sum of squares is 12.
Explanation of Solution
Calculation:
Degrees of freedom for treatment sum of squares:
If there are k treatments them the degrees of freedom for the treatment sum of squares is
Here, there are four brands (treatments), then the degrees of freedom is,
Substitute k as 4 in
Thus,
Thus, the degrees of freedom for the treatment sum of squares is 3.
Degrees of freedom for the error sum of squares:
The error sum of squares for the experiment with N observations and having k treatments is
There are four brands of treatments and each treatment is applied four times. Hence, there will be
Then the degrees of freedom is,
Substitute N as 16 and k as 4 in
Thus,
Thus, the degrees of freedom for the error sum of squares is 12.
c.
Find the P-value and give conclusion.
c.
Answer to Problem 1E
The P-value is 0.00037.
There is strong evidence to conclude that the mean number of un popped kernels is different for at least one of the four brands of popcorn.
Explanation of Solution
Calculation:
The given information is that, assume all the required conditions for ANOVA were satisfied.
The P-value is calculated as follows:
Software procedure:
Step by step procedure to find the P-value using MINITBA is given below:
- Choose Graph > Probability Distribution Plot > choose View Probability> OK.
- From Distribution, choose F.
- Enter Numerator df as 3 and Denominator df as 12.
- Under Shaded Area tab, select X Value and choose Right Tail.
- Enter the X Value as 13.56.
- Click OK.
Output obtained from MINITAB is given below:
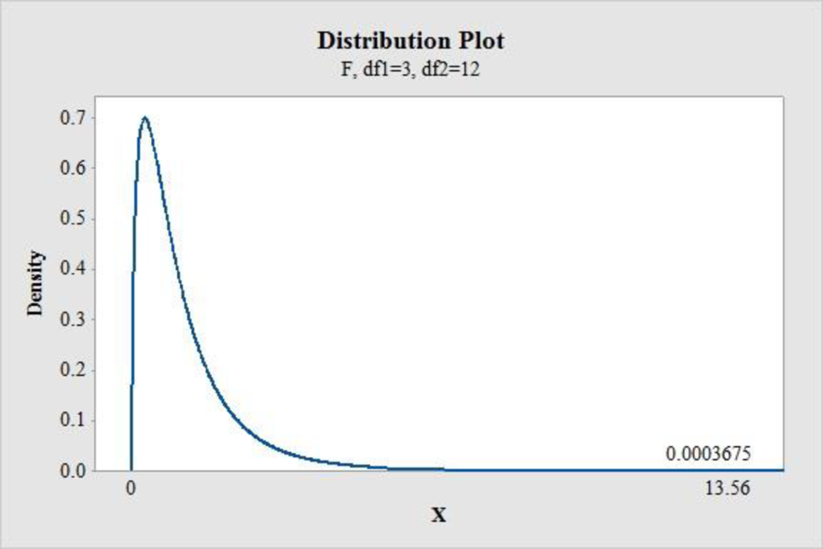
Conclusion:
The P-value for the F-statistic is 0.00037 and the level of significance is 0.01.
The P-value is less than the level of significance.
That is,
Thus, there is strong evidence to conclude that the mean number of unpopped kernels is different for at least one of the four brands of popcorn.
d.
Suggest what else about the data would be useful to check the assumptions and conditions.
d.
Explanation of Solution
The side by side boxplot of the treatments would be useful to check the similar variance conditions and also the spread of the data.
The normal probability of residuals can be used to check the normality assumption of the error term. If the points in the normal probability plot lies approximately on a straight line it assumed that the residuals are
Also, residual plot is used to identify pattern and spread of the residuals.
Want to see more full solutions like this?
Chapter 25 Solutions
Stats: Data and Models
- Harvard University California Institute of Technology Massachusetts Institute of Technology Stanford University Princeton University University of Cambridge University of Oxford University of California, Berkeley Imperial College London Yale University University of California, Los Angeles University of Chicago Johns Hopkins University Cornell University ETH Zurich University of Michigan University of Toronto Columbia University University of Pennsylvania Carnegie Mellon University University of Hong Kong University College London University of Washington Duke University Northwestern University University of Tokyo Georgia Institute of Technology Pohang University of Science and Technology University of California, Santa Barbara University of British Columbia University of North Carolina at Chapel Hill University of California, San Diego University of Illinois at Urbana-Champaign National University of Singapore McGill…arrow_forwardName Harvard University California Institute of Technology Massachusetts Institute of Technology Stanford University Princeton University University of Cambridge University of Oxford University of California, Berkeley Imperial College London Yale University University of California, Los Angeles University of Chicago Johns Hopkins University Cornell University ETH Zurich University of Michigan University of Toronto Columbia University University of Pennsylvania Carnegie Mellon University University of Hong Kong University College London University of Washington Duke University Northwestern University University of Tokyo Georgia Institute of Technology Pohang University of Science and Technology University of California, Santa Barbara University of British Columbia University of North Carolina at Chapel Hill University of California, San Diego University of Illinois at Urbana-Champaign National University of Singapore…arrow_forwardA company found that the daily sales revenue of its flagship product follows a normal distribution with a mean of $4500 and a standard deviation of $450. The company defines a "high-sales day" that is, any day with sales exceeding $4800. please provide a step by step on how to get the answers in excel Q: What percentage of days can the company expect to have "high-sales days" or sales greater than $4800? Q: What is the sales revenue threshold for the bottom 10% of days? (please note that 10% refers to the probability/area under bell curve towards the lower tail of bell curve) Provide answers in the yellow cellsarrow_forward
- Find the critical value for a left-tailed test using the F distribution with a 0.025, degrees of freedom in the numerator=12, and degrees of freedom in the denominator = 50. A portion of the table of critical values of the F-distribution is provided. Click the icon to view the partial table of critical values of the F-distribution. What is the critical value? (Round to two decimal places as needed.)arrow_forwardA retail store manager claims that the average daily sales of the store are $1,500. You aim to test whether the actual average daily sales differ significantly from this claimed value. You can provide your answer by inserting a text box and the answer must include: Null hypothesis, Alternative hypothesis, Show answer (output table/summary table), and Conclusion based on the P value. Showing the calculation is a must. If calculation is missing,so please provide a step by step on the answers Numerical answers in the yellow cellsarrow_forwardShow all workarrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





