
Concept explainers
(a)
ToFind: Expressions for the electric field and energy density as a function of the distance
(a)
Answer to Problem 44P
Explanation of Solution
Given information :
Radius of the wire =
Length of the wire =
Charge =
Inner radius of cylindrical shell =
Length of the cylindrical shell =
Charge =
Formula used :
From Gauss’s law:
Where, E electric field,
Energy density is given by:
Calculation:
Using Gauss’s law, find the electric field for cylindrical surfaces of radii
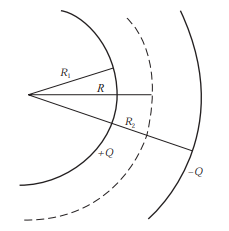
For
For
The energy density in the region
For
Because
Conclusion:
Electric field
Energy density
(b)
ToCalculate: The amount ofenergy that resides in a region between the conductors that has a radius
(b)
Answer to Problem 44P
Explanation of Solution
Given information:
Radius of the wire =
Length of the wire =
Charge =
Inner radius of cylindrical shell =
Length of the cylindrical shell =
Charge =
Formula used:
The energy residing in a cylindrical shell between the conductors of radius
Calculation:
Conclusion:
The amount ofenergy is:
(c)
To Calculate: The total energy stored in the capacitor.
(c)
Answer to Problem 44P
Explanation of Solution
Given information:
Radius of the wire =
Length of the wire =
Charge =
Inner radius of cylindrical shell =
Length of the cylindrical shell =
Charge =
Formula used:
Energy stored in the capacitor:
Where, C is the capacitance and V is the potential difference.
Calculation:
Integrate
Conclusion:
The total energy stored in the capacitor is:
Want to see more full solutions like this?
Chapter 24 Solutions
Physics for Scientists and Engineers
- Please help, everytime I try to input the data only one point shows on the graph. Graph of centripetal force, Fc, versus V E2 from Activity 1. Include a line of best fit and record the equation of the line.arrow_forwardBased on your graph, explain how centripetal force is affected when the hanging mass changes. Does your graph verify the relationship in the equation r = x^i + y^j = r cos ωt I + r sin ωt^j?arrow_forwardDid your experiment results in Data Table 3 verify, to within a reasonable experimental error, the condition of equilibrium of Equation 6: Στanti-clockwise = Στclockwise? Support your response with experimental data. My data shows that they are not equal to each other. So what does this mean? Thanks!arrow_forward
- Please help, everytime I try to input the data only one point shows on the graph. Graph of centripetal force, Fc, versus V E2 from Activity 1. Include a line of best fit and record the equation of the line.arrow_forwardExplain how your experiment met the condition for equilibrium in Equation 4: ΣFvertical = ΣFy = 0.arrow_forwardCan i get answer and solution for this question and can you teach me What we use to get the answer.arrow_forward
- Can i get answer and solution and can you teach me how to get it.arrow_forwardConsider a image that is located 30 cm in front of a lens. It forms an upright image 7.5 cm from the lens. Theillumination is so bright that that a faint inverted image, due to reflection off the front of the lens, is observedat 6.0 cm on the incident side of the lens. The lens is then turned around. Then it is observed that the faint,inverted image is now 10 cm on the incident side of the lens.What is the index of refraction of the lens?arrow_forward2. In class, we discussed several different flow scenarios for which we can make enough assumptions to simplify the Navier-Stokes equations enough to solve them and obtain an exact solution. Consulting the cylindrical form of the Navier-Stokes equations copied below, please answer the following questions. др a 1 a + +0x- + +O₂ = Pgr + μl 18²v, 2 ave ²v₁] az2 + at or r de r Əz dr ar Vodvz др [18 + + +Or + +Vz = Pgz +fl at ar r 20 ôz ôz dr ave дов V,Ve ave +Or + + = pge at dr r 80 Əz + az2 a.) In class, we discussed how the Navier-Stokes equations are an embodiment of Newton's 2nd law, F = ma (where bolded terms are vectors). Name the 3 forces that we are considering in our analysis of fluid flow for this class. др a 10 1 ve 2 av 2200] + +μ or 42 30 b.) If we make the assumption that flow is "fully developed" in the z direction, which term(s) would go to zero? Write the term below, describe what the term means in simple language (i.e. do not simply state "it is the derivative of a with…arrow_forward
- 1. Consult the form of the x-direction Navier-Stokes equation below that we discussed in class. (For this problem, only the x direction equation is shown for simplicity). Note that the equation provided is for a Cartesian coordinate system. In the spaces below, indicate which of the following assumptions would allow you to eliminate a term from the equation. If one of the assumptions provided would not allow you to eliminate a particular term, write "none" in the space provided. du ди at ( + + + 매일) du ди = - Pgx dy др dx ²u Fu u + fl + ax2 ay² az2 - дх - Əz 1 2 3 4 5 6 7 8 9 Assumption Flow is in the horizontal direction (e.g. patient lying on hospital bed) Flow is unidirectional in the x-direction Steady flow We consider the flow to be between two flat, infinitely wide plates There is no pressure gradient Flow is axisymmetric Term(s) in equationarrow_forwardDon't use ai to answer I will report you answerarrow_forwardwhy did the expert subtract the force exerted by the hand and the elbow by the force due to the weight of the hand and forearm and force exerted by the tricep. Does the order matter and how do you determine what to put first. Question 4 AP, CHAPTER 13 FROM BASIC BIOMECHANICS 8TH EDITIONarrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
 College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College





