
Concept explainers
Figure 24-24 shows eight particles that form a square, with distance d between adjacent particles. What is the net electric potential at point P at the center of the square if we take the electric potential to be zero at infinity?
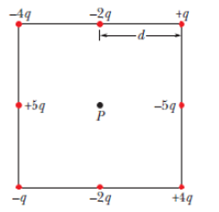
Figure 24-24 Question 1.
To find:
the net electric potential at P, the center of a square array of charged particles.
Answer to Problem 1Q
Solution:
The net electric potential at P is
Explanation of Solution
1) Concept
Electric potential obeys superposition principle. It means, the net potential at a point is the sum of potential contribution by each charge. Potential is written with the same sign as the charge contributing to it.
2) Formulae
i. Electric potential at a point due to a point charge q
Where k-
r- is the distance of the point from the charge
ii. Superposition of potential
Net electric potential= k Σ
3) Given
i. Fig. 24.24 showing 8 particles that form a square.
ii. Distance between two adjacent charges= d
iii. Charges at the top face from left to right: -4q, -2q, +q
iv. Charges at the bottom face from left to right: -q, -2q, +4q
v. Charge at the middle of left side=+5q
vi. Charge at the middle of right side=-5q
vii. Potential (V) is zero at infinity
4) Calculations
Corner particles are equidistant from the center.
Total charge of corner particles= -4q+q-q+4q=0
Therefore, the net potential at the center due to the corner particles is zero. Hence, the net potential is contributed only by the particles located in the middle of faces.
Using the formula and superposition of electric potential, the net potential
V=
=
The net electric potential at the center is
Conclusion:
Using the superposition of electric potential, net electric potential at the given point is determined.
Want to see more full solutions like this?
Chapter 24 Solutions
FUND. OF PHYSICS FOR LSU WILEY+ NEXT GEN
Additional Science Textbook Solutions
Introductory Chemistry (6th Edition)
Campbell Biology (11th Edition)
Principles of Anatomy and Physiology
College Physics: A Strategic Approach (3rd Edition)
Chemistry: The Central Science (14th Edition)
Human Physiology: An Integrated Approach (8th Edition)
- pls help on all asked questions kindlyarrow_forward19. Mount Everest, Earth's highest mountain above sea level, has a peak of 8849 m above sea level. Assume that sea level defines the height of Earth's surface. (re = 6.38 × 106 m, ME = 5.98 × 1024 kg, G = 6.67 × 10 -11 Nm²/kg²) a. Calculate the strength of Earth's gravitational field at a point at the peak of Mount Everest. b. What is the ratio of the strength of Earth's gravitational field at a point 644416m below the surface of the Earth to a point at the top of Mount Everest? C. A tourist watching the sunrise on top of Mount Everest observes a satellite orbiting Earth at an altitude 3580 km above his position. Determine the speed of the satellite.arrow_forwardpls help on allarrow_forward
- pls help on allarrow_forward6. As the distance between two charges decreases, the magnitude of the electric potential energy of the two-charge system: a) Always increases b) Always decreases c) Increases if the charges have the same sign, decreases if they have the opposite signs d) Increases if the charges have the opposite sign, decreases if they have the same sign 7. To analyze the motion of an elastic collision between two charged particles we use conservation of & a) Energy, Velocity b) Momentum, Force c) Mass, Momentum d) Energy, Momentum e) Kinetic Energy, Potential Energyarrow_forwardpls help on all asked questions kindlyarrow_forward
- pls help on all asked questions kindlyarrow_forward17. Two charges, one of charge +2.5 × 10-5 C and the other of charge +3.7 × 10-6 C, are 25.0 cm apart. The +2.5 × 10−5 C charge is to the left of the +3.7 × 10−6 C charge. a. Draw a diagram showing the point charges and label a point Y that is 20.0 cm to the left of the +3.7 × 10-6 C charge, on the line connecting the charges. (Field lines do not need to be drawn.) b. Calculate the net electric field at point Y.arrow_forward3arrow_forward
 College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
 Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





