
Concept explainers
Suppose you have the uniformly charged cube in FIGURE Q24.1. Can you use symmetry alone to deduce the shape of the cube 's electric field? If so, sketch and describe the field shape. If not, why not?

If symmetry alone can be used to deduce the shape of the cube’s electric field.
Explanation of Solution
Given:
The following figure of uniformly charged cube is given.

Using Gauss’s law, we can deduce electric fields, particularly those with a high degree of symmetry, simply from the shape of the charge distribution.
The pattern of the electric field through the surface is like that the shape of the charged body, if the Gaussian surface matches the symmetry of the charge dispersion inside. For a consistently charged dispersion, the shape of the Gaussian surface coincides with the shape of the electric field. So, the shape of the electric field is cubical in nature for a consistently charged cube shape that is the electric field at each point on the face of a solid shape is comparative and its direction is perpendicular to the face cube. The sketch of the electric field through each face of the consistently charged cube is appeared as follows.
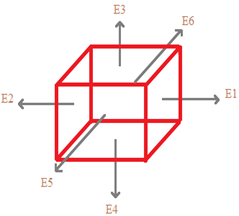
Conclusion:
We can use the symmetry alone to predict the shape of the electric field, the electric field in each face of the cube will have the same magnitude and perpendicular to that face.
Want to see more full solutions like this?
Chapter 24 Solutions
Physics for Scientists and Engineers: A Strategic Approach, Vol. 1 (Chs 1-21) (4th Edition)
Additional Science Textbook Solutions
Biology: Life on Earth (11th Edition)
Campbell Biology (11th Edition)
Chemistry: A Molecular Approach (4th Edition)
Chemistry: An Introduction to General, Organic, and Biological Chemistry (13th Edition)
Chemistry
Microbiology: An Introduction
- Solve and answer the question correctly please. Thank you!!arrow_forwardA spiral transition curve is used on railroads to connect a straight portion of the track with a curved portion. (Figure 1) Part A v = v₁ft/s 600 ft y = (106) x³ If the spiral is defined by the equation y = (106)³, where x and y are in feet, determine the magnitude of the acceleration of a train engine moving with a constant speed of v₁ = 30 ft/s when it is at point x = 600 ft. Express your answer to three significant figures and include the appropriate units. ? a = Value Unitsarrow_forwardsolve and answer the problem correctly please. Thank you!!arrow_forward
- Solve and answer the question correctly please. Thank you!!arrow_forwardSolve and answer the question correctly please. Thank you!!arrow_forwardWhen the motorcyclist is at A, he increases his speed along the vertical circular path at the rate of = (0.3t) ft/s², where t is in seconds. Take p = 360 ft. (Figure 1) Part A 60° Ρ B If he starts from rest at A, determine the magnitude of his velocity when he reaches B. Express your answer to three significant figures and include the appropriate units. v = Value Submit Request Answer ་ Part B ? Units If he starts from rest at A, determine the magnitude of his acceleration when he reaches B. Express your answer to three significant figures and include the appropriate units. 11 ? a = Value Unitsarrow_forward
- The car starts from rest at s = 0 and increases its speed at a₁ = 7 m/s². (Figure 1) Part A = 40 m Determine the time when the magnitude of acceleration becomes 20 m/s². Express your answer to three significant figures and include the appropriate units. ? t = Value Units Part B At what position s does this occur? Express your answer to three significant figures and include the appropriate units. s = Value Submit Request Answer ? Unitsarrow_forwardSolve and answer the question correctly please. Thank you!!arrow_forwardSolve and answer the question correctly please. Thank you!!arrow_forward
- Solve and answer the question correctly please. Thank you!!arrow_forwardSolve and answer the question correctly please. Thank you!!arrow_forwardr 2. Measuring Length mm 1 cm 2 3 INCH 1 16THS 5 6 7 8 9 10 11 FAIRGATE COLD SPRING, NEW YORK 2 3 12 1. Using the metric (top) scale only, what units are being used for the long lines with the numbers? Hint: Remember that 2.54 cm = 1 in. 2. What are the units of the small lines? 3. How many decimal places should be recorded using this tool? 4. What is the length of the red line? Note: Make sure to use the correct units and decimal places. 5. Now observe your ruler. What metric units are used on your ruler? 6. How many decimal places should you record when using your ruler? 7. Measure a box, book, coin and can and fill out the data table below. Make sure to use units and the correct number of decimal places for your ruler. Table 1: Measuring Length Data Table Object Length of the box Length Local PR Distribution Only $99/Release. Get Started On Our Website Now! V 2 217arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning




