Algebra and Trigonometry (6th Edition)
Algebra and Trigonometry (6th Edition)
6th Edition
ISBN: 9780134463216
Author: Robert F. Blitzer
Publisher: PEARSON
bartleby

Concept explainers

Correlation
Correlation defines a relationship between two independent variables. It tells the degree to which variables move in relation to each other. When two sets of data are related to each other, there is a correlation between them.
Linear Correlation
A correlation is used to determine the relationships between numerical and categorical variables. In other words, it is an indicator of how things are connected to one another. The correlation analysis is the study of how variables are related.
Regression Analysis
Regression analysis is a statistical method in which it estimates the relationship between a dependent variable and one or more independent variable. In simple terms dependent variable is called as outcome variable and independent variable is called as p…
bartleby

Videos

Textbook Question
Book Icon
Chapter 2.3, Problem 88E

Application Exercises

Americans are getting married later in life, or not getting married at all In 2010 more than half of Americans ages 25 through 29 were unmarried. The bar graph shows the percentage of never-married men and women in this age group for four selected years The data are displayed as two sets of four points each one scatterplot for the percentage of never-married American men and one for the percentage of never –married American women. Also shown for each scatter plot is a line that passes through of near the four points. Use these lines to solve Exercises 87-88

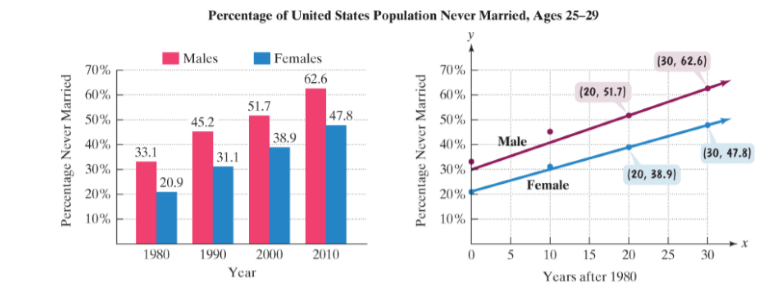
Chapter 2.3, Problem 88E, Application Exercises Americans are getting married later in life, or not getting married at all In

Source U.S. Census Bureasu

In this exercise, you win use the red line for the men shown on the scatter pw to develop a model for the percentage of never-married American males ages 25-29

a Use the two points whose coordinates are shown by the voice balloons to find the point-slope form of the equation of the line that models the percentage of never-married American males ages 25-29. y, x years after 1980.

b. Write the equation from part (a) in slope-intercept form. Use function notation

c. Use the linear function to predict the percentage of never-married American males, ages 25-29, in 2015.

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 2.3, Problem 87E
Next
Chapter 2.3, Problem 89E

Chapter 2 Solutions

Algebra and Trigonometry (6th Edition)

Ch. 2.1 - Fill in each blank so that the resulting statement...Ch. 2.1 - Fill in each blank so that the resulting statement...Ch. 2.1 - Fill in each blank so that the resulting statement...Ch. 2.1 - True or false: y=x21 1 defines y as a function of...Ch. 2.1 - Fill in each blank so that the resulting statement...Ch. 2.1 - Fill in each blank so that the resulting statement...Ch. 2.1 - Fill in each blank so that the resulting statement...Ch. 2.1 - 8. If any vertical line intersects a graph____ the...Ch. 2.1 - The shaded set of numbers shown on the x-axis can...Ch. 2.1 - Prob. 10CVC
Ch. 2.1 - Prob. 11CVCCh. 2.1 - 12. True or false: A function can have more than...Ch. 2.1 - In Exercises 1-10, determine whether each relation...Ch. 2.1 - In Exercises 1-10, determine whether each relation...Ch. 2.1 - In Exercises 1-10, determine whether each relation...Ch. 2.1 - In Exercises 1-10, determine whether each relation...Ch. 2.1 - In Exercises 1-10, determine whether each relation...Ch. 2.1 - In Exercises 1-10, determine whether each relation...Ch. 2.1 - In Exercises 1-10, determine whether each relation...Ch. 2.1 - In Exercises 1-10, determine whether each relation...Ch. 2.1 - In Exercises 1-10, determine whether each relation...Ch. 2.1 - In Exercises 1-10, determine whether each relation...Ch. 2.1 - In Exercises 11-26, determine whether each...Ch. 2.1 - In Exercises 11-26, determine whether each...Ch. 2.1 - In Exercises 11-26, determine whether each...Ch. 2.1 - In Exercises 11-26. determine whether each...Ch. 2.1 - In Exercises 11-26, determine whether each...Ch. 2.1 - In Exercises 11-26. determine whether each...Ch. 2.1 - In Exercises 11-26, determine whether each...Ch. 2.1 - In Exercises 11-26, determine whether each...Ch. 2.1 - In Exercises 11-26, determine whether each...Ch. 2.1 - In Exercises 11-26, determine whether each...Ch. 2.1 - In Exercises 11-26, determine whether each...Ch. 2.1 - In Exercises 11-26, determine whether each...Ch. 2.1 - In Exercises 11-26, determine whether each...Ch. 2.1 - In Exercises 11-26, determine whether each...Ch. 2.1 - In Exercises 11-26, determine whether each...Ch. 2.1 - In Exercises 11-26, determine whether each...Ch. 2.1 - In Exercises 27-38, evaluate each function at the...Ch. 2.1 - In Exercises 27-38, evaluate each function at the...Ch. 2.1 - In Exercises 27-38, evaluate each function at the...Ch. 2.1 - In Exercises 27-38, evaluate each function at the...Ch. 2.1 - In Exercises 27-38, evaluate each function at the...Ch. 2.1 - In Exercises 27-38, evaluate each function at the...Ch. 2.1 - In Exercises 27-38 evaluate each function at the...Ch. 2.1 - In Exercises 27-38, evaluate each function at the...Ch. 2.1 - In Exercises 27-38, evaluate each function at the...Ch. 2.1 - In Exercises 27-38, evaluate each function at the...Ch. 2.1 - In Exercises 27-38, evaluate each function at the...Ch. 2.1 - In Exercises 27-38, evaluate each function at the...Ch. 2.1 - In Exercises 39-50, graph the given functions, f...Ch. 2.1 - In Exercises 39-50, graph the given functions, f...Ch. 2.1 - In Exercises 39-50, graph the given functions, f...Ch. 2.1 - In Exercises 39-50, graph the given functions, f...Ch. 2.1 - In Exercises 39-50, graph the given functions, f...Ch. 2.1 - In Exercises 39-50, graph the given functions, f...Ch. 2.1 - In Exercises 39-50, graph the given functions, f...Ch. 2.1 - In Exercises 39-50, graph the given functions, f...Ch. 2.1 - In Exercises 39-50, graph the given functions, f...Ch. 2.1 - Prob. 48ECh. 2.1 - In Exercises 39-50, graph the given functions, f...Ch. 2.1 - In Exercises 39-50, graph the given functions, f...Ch. 2.1 - Prob. 51ECh. 2.1 - In Exercises 51-54, graph the given square root...Ch. 2.1 - In Exercises 51-54, graph the given square root...Ch. 2.1 - Prob. 54ECh. 2.1 - In Exercises 55-64, use the vertical line test to...Ch. 2.1 - In Exercises 55-64, use the vertical line test to...Ch. 2.1 - In Exercises 55-64, use the vertical line test to...Ch. 2.1 - In Exercises 55-64, use the vertical line test to...Ch. 2.1 - In Exercises 55-64, use the vertical line test to...Ch. 2.1 - In Exercises 55-64, use the vertical line test to...Ch. 2.1 - In Exercises 55-64, use the vertical line test to...Ch. 2.1 - In Exercises 55-64, use the vertical line test to...Ch. 2.1 - In Exercises 55-64, use the vertical line test to...Ch. 2.1 - In Exercises 55-64, use the vertical line test to...Ch. 2.1 - In Exercises 65-70, use the graph of f to find...Ch. 2.1 - In Exercises 65-70, use the graph of f to find...Ch. 2.1 - In Exercises 65-70, use the graph of f to find...Ch. 2.1 - In Exercises 65-70, use the graph of f to find...Ch. 2.1 - In Exercises 65-70, use the graph of f to find...Ch. 2.1 - In Exercises 65-70, use the graph of f to find...Ch. 2.1 - Use the graph of g to solve Exercises 71-76. Find...Ch. 2.1 - Use the graph of g to solve Exercises 71-76. Find...Ch. 2.1 - Use the graph of g to solve Exercises 71-76. 73....Ch. 2.1 - Use the graph of g to solve Exercises 71-76. 74....Ch. 2.1 - Use the graph of g to solve Exercises 71-76. For...Ch. 2.1 - Use the graph of g to solve Exercises 71-76. 76....Ch. 2.1 - In Exercises 77-92, use the graph to determine a....Ch. 2.1 - In Exercises 77-92, use the graph to determine a....Ch. 2.1 - In Exercises 77-92, use the graph to determine a....Ch. 2.1 - In Exercises 77-92, use the graph to determine a....Ch. 2.1 - In Exercises 77-92, use the graph to determine a....Ch. 2.1 - In Exercises 77-92, use the graph to determine a....Ch. 2.1 - In Exercises 77-92, use the graph to determine a....Ch. 2.1 - In Exercises 77-92, use the graph to determine a....Ch. 2.1 - In Exercises 77-92, use the graph to determine a....Ch. 2.1 - In Exercises 77-92, use the graph to determine a....Ch. 2.1 - In Exercises 77-92, use the graph to determine a....Ch. 2.1 - In Exercises 77-92, use the graph to determine a....Ch. 2.1 - Prob. 89ECh. 2.1 - In Exercises 77-92, use the graph to determine a....Ch. 2.1 - Prob. 91ECh. 2.1 - Prob. 92ECh. 2.1 - Prob. 93ECh. 2.1 - In Exercises 93-94,let and 94. Find and . Ch. 2.1 - Prob. 95ECh. 2.1 - Prob. 96ECh. 2.1 - Prob. 97ECh. 2.1 - Prob. 98ECh. 2.1 - Prob. 99ECh. 2.1 - Prob. 100ECh. 2.1 - The bar graph shows your chances of surviving to...Ch. 2.1 - The bar graph shows your chances of surviving to...Ch. 2.1 - Prob. 103ECh. 2.1 - The wage gap is used to compare the status of...Ch. 2.1 - In Exercises 105-108, you will be developing...Ch. 2.1 - In Exercises 105-108, you will be developing...Ch. 2.1 - In Exercises 105-108, you will be developing...Ch. 2.1 - Prob. 108ECh. 2.1 - Prob. 109ECh. 2.1 - Prob. 110ECh. 2.1 - Prob. 111ECh. 2.1 - Prob. 112ECh. 2.1 - Prob. 113ECh. 2.1 - Prob. 114ECh. 2.1 - Explain how to identify the domain and range of a...Ch. 2.1 - Prob. 116ECh. 2.1 - Prob. 117ECh. 2.1 - Make Sense? In Exercises 118-121, determine...Ch. 2.1 - Prob. 119ECh. 2.1 - Prob. 120ECh. 2.1 - Prob. 121ECh. 2.1 - Prob. 122ECh. 2.1 - Prob. 123ECh. 2.1 - Prob. 124ECh. 2.1 - Prob. 125ECh. 2.1 - 126. If find . Ch. 2.1 - Prob. 127ECh. 2.1 - If f(x+y)=f(x)+f(y) and f(1)=3, find f(2), f(3),...Ch. 2.1 - Prob. 129ECh. 2.1 - ACHIEVING SUCCESS According to the Ebbinghaus...Ch. 2.1 - ACHIEVING SUCCESS According to the Ebbinghaus...Ch. 2.1 - Prob. 132ECh. 2.1 - Prob. 133ECh. 2.1 - Exercises 132-134 will help you prepare for the...Ch. 2.2 - Assume that f is a function defined on an open...Ch. 2.2 - If f(a)f(x) in an open interval containing a, x ...Ch. 2.2 - The graph of an equation is symmetric with respect...Ch. 2.2 - 4. The graph of an equation is symmetric with...Ch. 2.2 - 5. The graph of an equation is symmetric with...Ch. 2.2 - 6. If f is an even function, then ____.The graph...Ch. 2.2 - 7. If f is an odd function, then ____. The graph...Ch. 2.2 - 8. A function defined by two or more equations...Ch. 2.2 - The greatest integer function is defined by...Ch. 2.2 - Fill in each blank so that the resulting statement...Ch. 2.2 - Fill in each blank so that the resulting statement...Ch. 2.2 - Fill in each blank so that the resulting statement...Ch. 2.2 - Practice Exercises In Exercises 1-12, use the...Ch. 2.2 - Practice Exercises In Exercises 1-12, use the...Ch. 2.2 - Practice Exercises In Exercises 1-12, use the...Ch. 2.2 - Practice Exercises In Exercises 1-12, use the...Ch. 2.2 - Practice Exercises In Exercises 1-12, use the...Ch. 2.2 - Practice Exercises In Exercises 1-12, use the...Ch. 2.2 - Practice Exercises In Exercises 1-12, use the...Ch. 2.2 - Practice Exercises In Exercises 1-12, use the...Ch. 2.2 - Practice Exercises In Exercises 1-12, use the...Ch. 2.2 - Practice Exercises In Exercises 1-12, use the...Ch. 2.2 - Practice Exercises In Exercises 1-12, use the...Ch. 2.2 - Practice Exercises In Exercises 1-12, use the...Ch. 2.2 - In Exercises 13-16, the graph of a function f is...Ch. 2.2 - In Exercises 13-16, the graph of a function f is...Ch. 2.2 - In Exercises 13-16, the graph of a function f is...Ch. 2.2 - In Exercises 23-16, the graph of a function f is...Ch. 2.2 - In Exercises 17-32, determine whether the graph of...Ch. 2.2 - In Exercises 17-32, determine whether the graph of...Ch. 2.2 - In Exercises 17-32, determine whether the graph of...Ch. 2.2 - In Exercises 17-32, determine whether the graph of...Ch. 2.2 - In Exercises 17-32, determine whether the graph of...Ch. 2.2 - In Exercises 17-32, determine whether the graph of...Ch. 2.2 - In Exercises 17 -32 , determine whether the graph...Ch. 2.2 - In Exercises 17 -32 , determine whether the graph...Ch. 2.2 - In Exercises 17-32, determine whether the graph of...Ch. 2.2 - In Exercises 17-32, determine whether the graph of...Ch. 2.2 - In Exercises 17-32, determine whether the graph of...Ch. 2.2 - In Exercises 17-32, determine whether the graph of...Ch. 2.2 - In Exercises 17-32, determine whether the graph of...Ch. 2.2 - In Exercises 17 -32 determine whether the graph...Ch. 2.2 - In Exercises 17-32, determine whether the graph of...Ch. 2.2 - In Exercises 17-32, determine whether the graph of...Ch. 2.2 - In Exercises 33-36, use possible symmetry to...Ch. 2.2 - In Exercises 33-36, use possible symmetry to...Ch. 2.2 - In Exercises 33-36, use possible symmetry to...Ch. 2.2 - In Exercises 33-36, use possible symmetry to...Ch. 2.2 - In Exercises 37-48, determine whether each...Ch. 2.2 - In Exercises 37-48, determine whether each...Ch. 2.2 - In Exercises 37-48, determine whether each...Ch. 2.2 - In Exercises 37-48, determine whether each...Ch. 2.2 - In Exercises 37-48, determine whether each...Ch. 2.2 - In Exercises 37-48, determine whether each...Ch. 2.2 - In Exercises 37-48, determine whether each...Ch. 2.2 - In Exercises 37-48, determine whether each...Ch. 2.2 - In Exercises 37-48, determine whether each...Ch. 2.2 - In Exercises 37-48, determine whether each...Ch. 2.2 - In Exercises 37-48, determine whether each...Ch. 2.2 - In Exercises 37-48, determine whether each...Ch. 2.2 - 49. Use the graph of f to determine each of the...Ch. 2.2 - 50. Use the graph of f to determine each of the...Ch. 2.2 - 51. Use the graph of f to determine each of the...Ch. 2.2 - Use the graph of f to determine each of the...Ch. 2.2 - In Exercise 53-58, evaluate each piecewise...Ch. 2.2 - In Exercise 53-58, evaluate each piecewise...Ch. 2.2 - In Exercise 53-58, evaluate each piecewise...Ch. 2.2 - In Exercise 53-58, evaluate each piecewise...Ch. 2.2 - In Exercise 53-58, evaluate each piecewise...Ch. 2.2 - In Exercise 53-58, evaluate each piecewise...Ch. 2.2 - In Exercises 59-70, the domain of each piecewise...Ch. 2.2 - In Exercises 59-70, the domain of each piecewise...Ch. 2.2 - In Exercises 59-70, the domain of each piecewise...Ch. 2.2 - In Exercises 59-70, the domain of each piecewise...Ch. 2.2 - In Exercises 59-70, the domain of each piecewise...Ch. 2.2 - In Exercises 59-70, the domain of each piecewise...Ch. 2.2 - In Exercises 59-70, the domain of each piecewise...Ch. 2.2 - In Exercises 59-70, the domain of each piecewise...Ch. 2.2 - In Exercises 59-70, the domain of each piecewise...Ch. 2.2 - In Exercises 59-70, the domain of each piecewise...Ch. 2.2 - In Exercises 59-70, the domain of each piecewise...Ch. 2.2 - In Exercises 59-70, the domain of each piecewise...Ch. 2.2 - In Exercises 71-92, find and simplify the...Ch. 2.2 - In Exercises 71-92, find and simplify the...Ch. 2.2 - In Exercises 71-92, find and simplify the...Ch. 2.2 - Prob. 74ECh. 2.2 - In Exercises 71-92, find and simplify the...Ch. 2.2 - Prob. 76ECh. 2.2 - In Exercises 71-92, find and simplify the...Ch. 2.2 - In Exercises 71-92, find and simplify the...Ch. 2.2 - Prob. 79ECh. 2.2 - Prob. 80ECh. 2.2 - In Exercises 71-92, find and simplify the...Ch. 2.2 - Prob. 82ECh. 2.2 - In Exercises 71-92, find and simplify the...Ch. 2.2 - In Exercises 71-92, find and simplify the...Ch. 2.2 - In Exercises 71-92, find and simplify the...Ch. 2.2 - Prob. 86ECh. 2.2 - Prob. 87ECh. 2.2 - Prob. 88ECh. 2.2 - In Exercises 71-92, find and simplify the...Ch. 2.2 - Prob. 90ECh. 2.2 - In Exercises 71-92, find and simplify the...Ch. 2.2 - Prob. 92ECh. 2.2 - Prob. 93ECh. 2.2 - Prob. 94ECh. 2.2 - A telephone company offers the following plans....Ch. 2.2 - Prob. 96ECh. 2.2 - Prob. 97ECh. 2.2 - In Exercises 97-98, write a piecewise function...Ch. 2.2 - Prob. 99ECh. 2.2 - Prob. 100ECh. 2.2 - Prob. 101ECh. 2.2 - Prob. 102ECh. 2.2 - With aging, body fat increases and muscle mass...Ch. 2.2 - With aging, body fat increases and muscle mass...Ch. 2.2 - With aging, body fat increases and muscle mass...Ch. 2.2 - With aging, body fat increases and muscle mass...Ch. 2.2 - Prob. 107ECh. 2.2 - Prob. 108ECh. 2.2 - Prob. 109ECh. 2.2 - Prob. 110ECh. 2.2 - Prob. 111ECh. 2.2 - Prob. 112ECh. 2.2 - Prob. 113ECh. 2.2 - Prob. 114ECh. 2.2 - 115. Furry Finances. A pet insurance policy has a...Ch. 2.2 - Prob. 116ECh. 2.2 - 117. Suppose that a function f whose graph...Ch. 2.2 - Prob. 118ECh. 2.2 - Prob. 119ECh. 2.2 - Prob. 120ECh. 2.2 - Prob. 121ECh. 2.2 - Prob. 122ECh. 2.2 - Prob. 123ECh. 2.2 - Explain how to find the difference quotient of a...Ch. 2.2 - Prob. 125ECh. 2.2 - Prob. 126ECh. 2.2 - Prob. 127ECh. 2.2 - Prob. 128ECh. 2.2 - Prob. 129ECh. 2.2 - Prob. 130ECh. 2.2 - Prob. 131ECh. 2.2 - Prob. 132ECh. 2.2 - Prob. 133ECh. 2.2 - Make Sense? In Exercises 133-136, determine...Ch. 2.2 - Prob. 135ECh. 2.2 - Prob. 136ECh. 2.2 - 137. Sketch the graph of f using the following...Ch. 2.2 - Define a piece wise function on the intervals (,...Ch. 2.2 - Prob. 139ECh. 2.2 - Prob. 140ECh. 2.2 - Prob. 141ECh. 2.2 - Prob. 142ECh. 2.2 - Prob. 143ECh. 2.2 - Prob. 144ECh. 2.2 - Prob. 145ECh. 2.3 - Data presented in a visual form as a set of points...Ch. 2.3 - 2. The slope, m, of a line through the distinct...Ch. 2.3 - If a line rises from left to right, the line has...Ch. 2.3 - 4. If a line falls from left to right, the line...Ch. 2.3 - 5. The slope of a horizontal line is ____. Ch. 2.3 - The slope of a vertical line is ____.Ch. 2.3 - The point-slope form of the equation of a...Ch. 2.3 - The slope-intercept form of the equation of a line...Ch. 2.3 - 9. In order to graph the line whose equation is ,...Ch. 2.3 - The graph of the equation y=3 is a/an ____ line.Ch. 2.3 - 11. The graph of the equation is a/an ____ line. Ch. 2.3 - Fill in each blank so that the resulting statement...Ch. 2.3 - In Exercises 1-10, find the slope of the line...Ch. 2.3 - In Exercises 1-10, find the slope of the line...Ch. 2.3 - In Exercises 1-10, find the slope of the line...Ch. 2.3 - In Exercises 1-10, find the slope of the line...Ch. 2.3 - In Exercises 1-10, find the slope of the line...Ch. 2.3 - In Exercises 1-10, find the slope of the line...Ch. 2.3 - In Exercises 1-10, find the slope of the line...Ch. 2.3 - In Exercises 1-10, find the slope of the line...Ch. 2.3 - In Exercises 1-10, find the slope of the line...Ch. 2.3 - In Exercises 1-10, find the slope of the line...Ch. 2.3 - In Exercises 11-38, use the given conditions to...Ch. 2.3 - Prob. 12ECh. 2.3 - In Exercises 11-38, use the given conditions to...Ch. 2.3 - Prob. 14ECh. 2.3 - Prob. 15ECh. 2.3 - Prob. 16ECh. 2.3 - In Exercises 11-38, use the given conditions to...Ch. 2.3 - Prob. 18ECh. 2.3 - Prob. 19ECh. 2.3 - Prob. 20ECh. 2.3 - Slope=12, passing through the originCh. 2.3 - Prob. 22ECh. 2.3 - Prob. 23ECh. 2.3 - Prob. 24ECh. 2.3 - Prob. 25ECh. 2.3 - Prob. 26ECh. 2.3 - Prob. 27ECh. 2.3 - Prob. 28ECh. 2.3 - Prob. 29ECh. 2.3 - Prob. 30ECh. 2.3 - Prob. 31ECh. 2.3 - Prob. 32ECh. 2.3 - In Exercises 11-38, use the given conditions to...Ch. 2.3 - Prob. 34ECh. 2.3 - In Exercises 11-38, use the given conditions to...Ch. 2.3 - In Exercises 11-38, use the given conditions to...Ch. 2.3 - In Exercises 11-38, use the given conditions to...Ch. 2.3 - In Exercises 11-38, use the given conditions to...Ch. 2.3 - In Exercises 39-48, give the slope and y-intercept...Ch. 2.3 - Prob. 40ECh. 2.3 - In Exercises 39-48, give the slope and y-intercept...Ch. 2.3 - Prob. 42ECh. 2.3 - Prob. 43ECh. 2.3 - Prob. 44ECh. 2.3 - In Exercises 39-48, give the slope and y-intercept...Ch. 2.3 - Prob. 46ECh. 2.3 - Prob. 47ECh. 2.3 - Prob. 48ECh. 2.3 - In Exercises 49-58, graph each equation in a...Ch. 2.3 - Prob. 50ECh. 2.3 - Prob. 51ECh. 2.3 - Prob. 52ECh. 2.3 - In Exercises 49-58, graph each equation in a...Ch. 2.3 - Prob. 54ECh. 2.3 - In Exercises 49-58, graph each equation in a...Ch. 2.3 - In Exercises 49-58, graph each equation in a...Ch. 2.3 - In Exercises 49-58, graph each equation in a...Ch. 2.3 - In Exercises 49-58, graph each equation in a...Ch. 2.3 - Prob. 59ECh. 2.3 - Prob. 60ECh. 2.3 - In Exercises 59-66, a. Rewrite the given equation...Ch. 2.3 - Prob. 62ECh. 2.3 - Prob. 63ECh. 2.3 - Prob. 64ECh. 2.3 - In Exercises 59-66, a. Rewrite the given equation...Ch. 2.3 - In Exercises 59-66, a. Rewrite the given equation...Ch. 2.3 - In Exercises 67-72, use intercepts to graph each...Ch. 2.3 - Prob. 68ECh. 2.3 - In Exercises 67-72, use intercepts to graph each...Ch. 2.3 - Prob. 70ECh. 2.3 - Prob. 71ECh. 2.3 - Prob. 72ECh. 2.3 - In Exercises 73-76, find the slope of the line...Ch. 2.3 - Prob. 74ECh. 2.3 - In Exercises 73-76, find the slope of the line...Ch. 2.3 - Prob. 76ECh. 2.3 - In Exercises 79-80, find the value of y if the...Ch. 2.3 - Prob. 78ECh. 2.3 - Prob. 79ECh. 2.3 - Prob. 80ECh. 2.3 - Prob. 81ECh. 2.3 - In Exercises 81 -82 , graph each linear...Ch. 2.3 - Prob. 83ECh. 2.3 - Prob. 84ECh. 2.3 - Prob. 85ECh. 2.3 - Prob. 86ECh. 2.3 - Application Exercises Americans are getting...Ch. 2.3 - Application Exercises Americans are getting...Ch. 2.3 - Prob. 89ECh. 2.3 - Prob. 90ECh. 2.3 - Shown, again, is the scatter plot that indicates a...Ch. 2.3 - Prob. 92ECh. 2.3 - Prob. 93ECh. 2.3 - Prob. 94ECh. 2.3 - Prob. 95ECh. 2.3 - Prob. 96ECh. 2.3 - Prob. 97ECh. 2.3 - Prob. 98ECh. 2.3 - Prob. 99ECh. 2.3 - Prob. 100ECh. 2.3 - Prob. 101ECh. 2.3 - Prob. 102ECh. 2.3 - Prob. 103ECh. 2.3 - 104. Is there a relationship between wine...Ch. 2.3 - Prob. 105ECh. 2.3 - Prob. 106ECh. 2.3 - Prob. 107ECh. 2.3 - Prob. 108ECh. 2.3 - In Exercises 109-112, determine whether each...Ch. 2.3 - Prob. 110ECh. 2.3 - Prob. 111ECh. 2.3 - Prob. 112ECh. 2.3 - Prob. 113ECh. 2.3 - In Exercises 113-114, find the coefficients that...Ch. 2.3 - 115. Prove that the equation of a line passing...Ch. 2.3 - Prob. 116ECh. 2.3 - Prob. 117ECh. 2.3 - Prob. 118ECh. 2.3 - Prob. 119ECh. 2.3 - Prob. 120ECh. 2.3 - Prob. 121ECh. 2.3 - Prob. 122ECh. 2.3 - Exercises 121-123 will help you prepare for the...Ch. 2.4 - Fill in each blank so that the resulting...Ch. 2.4 - Fill in each blank so that the resulting statement...Ch. 2.4 - Fill in each blank so that the resulting statement...Ch. 2.4 - Fill in each blank so that the resulting statement...Ch. 2.4 - Fill in each blank so that the resulting statement...Ch. 2.4 - Fill in each blank so that the resulting statement...Ch. 2.4 - In Exercises 1-4, write an equation for line L in...Ch. 2.4 - In Exercises 1-4, write an equation for line L in...Ch. 2.4 - In Exercises 1-4, write an equation for line L in...Ch. 2.4 - In Exercises 1-4, write an equation for line L in...Ch. 2.4 - In Exercises 5-8, use the given conditions to...Ch. 2.4 - In Exercises 5-8, use the given conditions to...Ch. 2.4 - In Exercises 5-8, use the given conditions to...Ch. 2.4 - In Exercises 5-8. use the given conditions to...Ch. 2.4 - In Exercises 9-12, use the given conditions to...Ch. 2.4 - In Exercises 9-12, use the given conditions to...Ch. 2.4 - In Exercises 9-12, use the given conditions to...Ch. 2.4 - In Exercises 9-12, use the given conditions to...Ch. 2.4 - In Exercises 13-18, find the average rate of...Ch. 2.4 - In Exercises 13-18, find the average rate of...Ch. 2.4 - In Exercises 13-18, find the average rate of...Ch. 2.4 - In Exercises 13-I8, find the average rate of...Ch. 2.4 - In Exercises 13-18, find the average rate of...Ch. 2.4 - Prob. 18ECh. 2.4 - In Exercises19-24, write an equation in...Ch. 2.4 - In Exercises 19-24, write an equation in...Ch. 2.4 - In Exercises 19-24, write an equation in...Ch. 2.4 - In Exercises 19-24, write an equation in...Ch. 2.4 - In Exercises 19-24, write an equation in...Ch. 2.4 - In Exercises 19-24, write an equation in...Ch. 2.4 - In Exercises 25-26, find a linear function in...Ch. 2.4 - In Exercises 25-26, find a linear function in...Ch. 2.4 - The stated intent of the 1994 "don't ask, don't...Ch. 2.4 - The stated intent of the 1994 “don't ask, don't...Ch. 2.4 - The function f(x)=1.1x335x2+264x+557 models the...Ch. 2.4 - Prob. 30ECh. 2.4 - Prob. 31ECh. 2.4 - Prob. 32ECh. 2.4 - 33. If you know a point on a line and you know the...Ch. 2.4 - Prob. 34ECh. 2.4 - Explaining the Concepts What is a secant line?Ch. 2.4 - Explaining the Concepts What is the average rate...Ch. 2.4 - Prob. 37ECh. 2.4 - Prob. 38ECh. 2.4 - Make Sense? In Exercises 38-41, determine whether...Ch. 2.4 - Prob. 40ECh. 2.4 - Make Sense? In Exercises 38-41, determine whether...Ch. 2.4 - Prob. 42ECh. 2.4 - Prob. 43ECh. 2.4 - 44. Solve and check: . (Section 1.2, Example 2) Ch. 2.4 - Prob. 45ECh. 2.4 - Prob. 46ECh. 2.4 - Exercises 47-49 will help you prepare for the...Ch. 2.4 - Prob. 48ECh. 2.4 - Prob. 49ECh. 2.5 - The graph of y=f(x)5 is obtained by a/an ____shift...Ch. 2.5 - Fill in each blank so that the resulting statement...Ch. 2.5 - Fill in each blank so that the resulting statement...Ch. 2.5 - Fill in each blank so that the resulting statement...Ch. 2.5 - The graph of y=5f(x) is obtained by a/an ____...Ch. 2.5 - Fill in each blank so that the resulting statement...Ch. 2.5 - Fill in each blank so that the resulting statement...Ch. 2.5 - In Exercises 1-16. use the graph of y=f(x) to...Ch. 2.5 - In Exercises1-16, use the graph of to graph each...Ch. 2.5 - In Exercises 1-16, use the graph of y=f(x) to...Ch. 2.5 - In Exercises 1-16, use the graph of to graph each...Ch. 2.5 - In Exercises 1-16, use the graph of to graph each...Ch. 2.5 - In Exercises 1-16, use the graph of y=f(x) to...Ch. 2.5 - In Exercises 1-16, use the graph of to graph each...Ch. 2.5 - Prob. 8ECh. 2.5 - In Exercises 1-16, use the graph of y=f(x) to...Ch. 2.5 - Prob. 10ECh. 2.5 - In Exercises 1-16. use the graph of y=f(x) to...Ch. 2.5 - In Exercises 1-16, use the graph of to graph each...Ch. 2.5 - In Exercises 1-16, use the graph of to graph each...Ch. 2.5 - In Exercises 1-16, use the graph of to graph each...Ch. 2.5 - Prob. 15ECh. 2.5 - Prob. 16ECh. 2.5 - In Exercises 17-32, use the graph of to graph...Ch. 2.5 - In Exercises 17-32, use the graph of to graph...Ch. 2.5 - In Exercises 17-32, use the graph of y=f(x) to...Ch. 2.5 - In Exercises 17-32, use the graph of to graph...Ch. 2.5 - In Exercises 17-32, use the graph of to graph...Ch. 2.5 - In Exercises 17-32, use the graph of to graph...Ch. 2.5 - In Exercises 17-32, use the graph of y=f(x) to...Ch. 2.5 - In Exercises 17-32, use the graph of to graph...Ch. 2.5 - In Exercises 17-32, use the graph of to graph...Ch. 2.5 - In Exercises 17-32, use the graph of y=f(x) to...Ch. 2.5 - In Exercises 17-32, use the graph of y=f(x) to...Ch. 2.5 - In Exercises 17-32, use the graph of y=f(x) to...Ch. 2.5 - In Exercises 17-32, use the graph of y=f(x) to...Ch. 2.5 - In Exercises 17-32, use the graph of y=f(x) to...Ch. 2.5 - In Exercises 17-32, use the graph of to graph...Ch. 2.5 - Prob. 32ECh. 2.5 - In Exercises 33-44, use the graph of to graph...Ch. 2.5 - Prob. 34ECh. 2.5 - Prob. 35ECh. 2.5 - Prob. 36ECh. 2.5 - In Exercises 33-44, use the graph of y=f(x) to...Ch. 2.5 - Prob. 38ECh. 2.5 - Prob. 39ECh. 2.5 - Prob. 40ECh. 2.5 - In Exercises 33-44, use the graph of to graph...Ch. 2.5 - Prob. 42ECh. 2.5 - Prob. 43ECh. 2.5 - Prob. 44ECh. 2.5 - In Exercises 45-52, use the graph of to graph...Ch. 2.5 - In Exercises 45-52, use the graph of y=f(x) to...Ch. 2.5 - Prob. 47ECh. 2.5 - Prob. 48ECh. 2.5 - In Exercises 45-52, use the graph of y=f(x) to...Ch. 2.5 - In Exercises 45-52, use the graph of y=f(x) to...Ch. 2.5 - In Exercises 45-52, use the graph of to graph...Ch. 2.5 - Prob. 52ECh. 2.5 - Prob. 53ECh. 2.5 - In Exercise 53-66, begin by graphing the standard...Ch. 2.5 - In Exercise 53-66, begin by graphing the standard...Ch. 2.5 - In Exercise 53-66, begin by graphing the standard...Ch. 2.5 - In Exercise 53-66, begin by graphing the standard...Ch. 2.5 - In Exercise 53-66, begin by graphing the standard...Ch. 2.5 - In Exercise 53-66, begin by graphing the standard...Ch. 2.5 - In Exercise 53-66, begin by graphing the standard...Ch. 2.5 - In Exercise 53-66, begin by graphing the standard...Ch. 2.5 - In Exercise 53-66, begin by graphing the standard...Ch. 2.5 - In Exercise 53-66, begin by graphing the standard...Ch. 2.5 - In Exercise 53-66, begin by graphing the standard...Ch. 2.5 - In Exercise 53-66, begin by graphing the standard...Ch. 2.5 - In Exercise 53-66, begin by graphing the standard...Ch. 2.5 - In Exercises 67-80, begin by graphing the square...Ch. 2.5 - In Exercises 67-80, begin by graphing the square...Ch. 2.5 - In Exercises 67-80, begin by graphing the square...Ch. 2.5 - In Exercises 67-80, begin by graphing the square...Ch. 2.5 - In Exercises 67-80, begin by graphing the square...Ch. 2.5 - In Exercises 67-80, begin by graphing the square...Ch. 2.5 - In Exercises 67-80, begin by graphing the square...Ch. 2.5 - In Exercises 67-80, begin by graphing the square...Ch. 2.5 - In Exercises 67-80, begin by graphing the square...Ch. 2.5 - In Exercises 67-80, begin by graphing the square...Ch. 2.5 - In Exercises 67-80, begin by graphing the square...Ch. 2.5 - In Exercises 67-80, begin by graphing the square...Ch. 2.5 - In Exercises 67-80, begin by graphing the square...Ch. 2.5 - In Exercises 67-80, begin by graphing the square...Ch. 2.5 - Prob. 81ECh. 2.5 - In Exercises 81-94, begin by graphing the absolute...Ch. 2.5 - In Exercises 81-94, begin by graphing the absolute...Ch. 2.5 - In Exercises 81-94, begin by graphing the absolute...Ch. 2.5 - In Exercises 81-94, begin by graphing the absolute...Ch. 2.5 - In Exercises 81-94, begin by graphing the absolute...Ch. 2.5 - In Exercises 81-94, begin by graphing the absolute...Ch. 2.5 - In Exercises 81-94, begin by graphing the absolute...Ch. 2.5 - In Exercises 81-94, begin by graphing the absolute...Ch. 2.5 - In Exercises 81-94, begin by graphing the absolute...Ch. 2.5 - In Exercises 81-94, begin by graphing the absolute...Ch. 2.5 - In Exercises 81-94, begin by graphing the absolute...Ch. 2.5 - In Exercises 81-94, begin by graphing the absolute...Ch. 2.5 - In Exercises 81-94, begin by graphing the absolute...Ch. 2.5 - In Exercises 95-106, begin by graphing the...Ch. 2.5 - In Exercises 95-106, begin by graphing the...Ch. 2.5 - In Exercises 95-106, begin by graphing the...Ch. 2.5 - In Exercises 95-106, begin by graphing the...Ch. 2.5 - In Exercises 95-106, begin by graphing the...Ch. 2.5 - In Exercises 95-106, begin by graphing the...Ch. 2.5 - In Exercises 95-106, begin by graphing the...Ch. 2.5 - In Exercises 95-106, begin by graphing the...Ch. 2.5 - In Exercises 95-106, begin by graphing the...Ch. 2.5 - In Exercises 95-106, begin by graphing the...Ch. 2.5 - In Exercises 95-106, begin by graphing the...Ch. 2.5 - In Exercises 95-106, begin by graphing the...Ch. 2.5 - In Exercises 107-118, begin by graphing the cube...Ch. 2.5 - In Exercises 107-118, begin by graphing the cube...Ch. 2.5 - In Exercises 107-118, begin by graphing the cube...Ch. 2.5 - Prob. 110ECh. 2.5 - Prob. 111ECh. 2.5 - Prob. 112ECh. 2.5 - In Exercises 107-118, begin by graphing the cube...Ch. 2.5 - Prob. 114ECh. 2.5 - Prob. 115ECh. 2.5 - Prob. 116ECh. 2.5 - Prob. 117ECh. 2.5 - Prob. 118ECh. 2.5 - Prob. 119ECh. 2.5 - Prob. 120ECh. 2.5 - Prob. 121ECh. 2.5 - Prob. 122ECh. 2.5 - Prob. 123ECh. 2.5 - Prob. 124ECh. 2.5 - Prob. 125ECh. 2.5 - Prob. 126ECh. 2.5 - 127. The function models the median height, f(x),...Ch. 2.5 - Prob. 128ECh. 2.5 - Explaining the Concepts What must be done to a...Ch. 2.5 - Explaining the Concepts What must be done to a...Ch. 2.5 - Prob. 131ECh. 2.5 - Prob. 132ECh. 2.5 - Prob. 133ECh. 2.5 - Prob. 134ECh. 2.5 - Prob. 135ECh. 2.5 - 136. a. Use a graphing utility to graph . b. Graph...Ch. 2.5 - Make Sense? During the winter, you program your...Ch. 2.5 - Make Sense? During the winter, you program your...Ch. 2.5 - Make Sense? During the winter, you program your...Ch. 2.5 - Make Sense? During the winter, you program your...Ch. 2.5 - In Exercises 141-144, determine whether each...Ch. 2.5 - In Exercises 141-144, determine whether each...Ch. 2.5 - In Exercises 141-144, determine whether each...Ch. 2.5 - In Exercises 141-144, determine whether each...Ch. 2.5 - In Exercises 145-148, functions f and g are...Ch. 2.5 - Prob. 146ECh. 2.5 - Prob. 147ECh. 2.5 - Prob. 148ECh. 2.5 - Prob. 149ECh. 2.5 - Prob. 150ECh. 2.5 - Prob. 151ECh. 2.5 - For Exercises 149-152, assume that (a, b) is a...Ch. 2.5 - Prob. 153ECh. 2.5 - Prob. 154ECh. 2.5 - Multiply and write the product in standard form:...Ch. 2.5 - In Exercises 156-157, perform the indicated...Ch. 2.5 - Prob. 157ECh. 2.5 - Prob. 158ECh. 2.6 - 1. We exclude from a function's domain real...Ch. 2.6 - 2. We exclude from a function's domain real...Ch. 2.6 - Fill in each blank so that the resulting statement...Ch. 2.6 - Fill in each blank so that the resulting statement...Ch. 2.6 - Fill in each blank so that the resulting statement...Ch. 2.6 - Fill in each blank so that the resulting statement...Ch. 2.6 - Fill in each blank so that the resulting statement...Ch. 2.6 - Prob. 8CVCCh. 2.6 - Prob. 9CVCCh. 2.6 - The notation fg, called the _________ of the...Ch. 2.6 - Prob. 11CVCCh. 2.6 - Prob. 12CVCCh. 2.6 - Prob. 13CVCCh. 2.6 - Prob. 14CVCCh. 2.6 - Prob. 15CVCCh. 2.6 - Fill in each blank so that the resulting statement...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - Prob. 8ECh. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 1-30, find the domain of each...Ch. 2.6 - In Exercises 31-50, find , and . Determine the...Ch. 2.6 - In Exercises 31-50, find , and . Determine the...Ch. 2.6 - In Exercises 31-50, find f+g,fg,fg , and 1g ....Ch. 2.6 - In Exercises 31-50, find , and . Determine the...Ch. 2.6 - In Exercises 31-50, find f+g,fg,fg , and 1g ....Ch. 2.6 - In Exercises 31-50, find , and . Determine the...Ch. 2.6 - In Exercises 31-50, find , and . Determine the...Ch. 2.6 - In Exercises 31-50, find , and . Determine the...Ch. 2.6 - In Exercises 31-50, find f+g,fg,fg , and 1g ....Ch. 2.6 - In Exercises 31-50, find , and . Determine the...Ch. 2.6 - In Exercises 31-50, find , and. Determine the...Ch. 2.6 - In Exercises 31-50, find , and . Determine the...Ch. 2.6 - In Exercises 31-50, find f+g,fg,fg , and 1g ....Ch. 2.6 - In Exercises 31-50, find f+g,fg,fg , and 1g ....Ch. 2.6 - In Exercises 31-50, find f+g,fg,fg , and 1g ....Ch. 2.6 - In Exercises 31-50, find , and . Determine the...Ch. 2.6 - In Exercises 31-50, find f+g,fg,fg , and 1g ....Ch. 2.6 - In Exercises 31-50, find , and . Determine the...Ch. 2.6 - In Exercises 31-50, find , and . Determine the...Ch. 2.6 - In Exercises 31-50, find f+g,fg,fg , and 1g ....Ch. 2.6 - In Exercises 51-66, find a. (fg)(x) b. (gf)(x) c....Ch. 2.6 - In Exercises 51-66, find a. (fg)(x) b. (gf)(x) c....Ch. 2.6 - In Exercises 51-66, find a. b. c. d. 53. Ch. 2.6 - In Exercises 51-66, find a. (fg)(x) b. (gf)(x) c....Ch. 2.6 - In Exercises 51-66, find a. b. c. d. . 55. Ch. 2.6 - In Exercises 51-66, find a. (fg)(x) b. (gf)(x) c....Ch. 2.6 - In Exercises 51-66, find a. (fg)(x) b. (gf)(x) c....Ch. 2.6 - In Exercises 51-66, find a. (fg)(x) b. (gf)(x) c....Ch. 2.6 - In Exercises 51-66, find a. (fg)(x) b. (gf)(x) c....Ch. 2.6 - In Exercises 51-66, find a. (fg)(x) b. (gf)(x) c....Ch. 2.6 - Prob. 61ECh. 2.6 - In Exercises 51-66, find a. (fg)(x) b. (gf)(x) c....Ch. 2.6 - In Exercises 51-66, find a. b. c. d. . 63. Ch. 2.6 - In Exercises 51-66, find a. (fg)(x) b. (gf)(x) c....Ch. 2.6 - In Exercises 51-66, find a. b. c. d. . 65. Ch. 2.6 - In Exercises 51-66, find a. (fg)(x) b. (gf)(x) c....Ch. 2.6 - In Exercises 67-74, find a. b. the domain of...Ch. 2.6 - In Exercises 67-74, find a. (fg)(x) b. the domain...Ch. 2.6 - In Exercises 67-74, find a. (fg)(x) b. the domain...Ch. 2.6 - In Exercises 67-74, find a. (fg)(x) b. the domain...Ch. 2.6 - In Exercises 67-74, find a. b. the domain of...Ch. 2.6 - In Exercises 67-74, find a. (fg)(x) b. the domain...Ch. 2.6 - In Exercises 67-74, find a. (fg)(x) b. the domain...Ch. 2.6 - In Exercises 67-74, find a. (fg)(x) b. the domain...Ch. 2.6 - In Exercises 75-82, express the given function h...Ch. 2.6 - Prob. 76ECh. 2.6 - In Exercises 75-82, express the given function h...Ch. 2.6 - Prob. 78ECh. 2.6 - In Exercises 75-82, express the given function h...Ch. 2.6 - Prob. 80ECh. 2.6 - In Exercises 75-82, express the given function h...Ch. 2.6 - Prob. 82ECh. 2.6 - Practice Plus Use the graphs of f and g to solve...Ch. 2.6 - Practice Plus Use the graphs of f and g to solve...Ch. 2.6 - Practice Plus Use the graphs of f and g to solve...Ch. 2.6 - Practice Plus Use the graphs of f and g to solve...Ch. 2.6 - Practice Plus Use the graphs of f and g to solve...Ch. 2.6 - Practice Plus Use the graphs of f and g to solve...Ch. 2.6 - Prob. 89ECh. 2.6 - Prob. 90ECh. 2.6 - In Exercises 91-94, use the graphs of f and g to...Ch. 2.6 - In Exercises 91-94, use the graphs of f and g to...Ch. 2.6 - In Exercises 91-94, use the graphs of f and g to...Ch. 2.6 - In Exercises 91-94, use the graphs of f and g to...Ch. 2.6 - In Exercises 95-96, find all values of x...Ch. 2.6 - Prob. 96ECh. 2.6 - The bar graph shows the population of the United...Ch. 2.6 - The bar graph shows the population of the United...Ch. 2.6 - Prob. 99ECh. 2.6 - Prob. 100ECh. 2.6 - Prob. 101ECh. 2.6 - The regular price of a pair of jeans is x dollars....Ch. 2.6 - Prob. 103ECh. 2.6 - Prob. 104ECh. 2.6 - Prob. 105ECh. 2.6 - Prob. 106ECh. 2.6 - Prob. 107ECh. 2.6 - Prob. 108ECh. 2.6 - Prob. 109ECh. 2.6 - Prob. 110ECh. 2.6 - Prob. 111ECh. 2.6 - Prob. 112ECh. 2.6 - Prob. 113ECh. 2.6 - Prob. 114ECh. 2.6 - Prob. 115ECh. 2.6 - In Exercises 114-117, determine whether each...Ch. 2.6 - Prob. 117ECh. 2.6 - Prove than if f and g are even functions, then fg...Ch. 2.6 - Prob. 119ECh. 2.6 - Prob. 120ECh. 2.6 - Prob. 121ECh. 2.6 - Prob. 122ECh. 2.6 - Prob. 123ECh. 2.6 - Prob. 124ECh. 2.6 - Prob. 125ECh. 2.7 - 1. The notation means the ____ of the function...Ch. 2.7 - 2. If the function g is the inverse of the...Ch. 2.7 - 3. A function f has an inverse that is a function...Ch. 2.7 - The graph of f1 is a reflection of the graph of f...Ch. 2.7 - In Exercises 1-10, find f(g(x)) and g(f(x)) and...Ch. 2.7 - In Exercises 1-10, find f(g(x)) and g(f(x)) and...Ch. 2.7 - In Exercises 1-10, find f(g(x)) and g(f(x)) and...Ch. 2.7 - In Exercises 1-10, find f(g(x)) and g(f(x)) and...Ch. 2.7 - In Exercises 1-10, find f(g(x)) and g(f(x)) and...Ch. 2.7 - In Exercises 1-10, find f(g(x)) and g(f(x)) and...Ch. 2.7 - In Exercises 1-10, find f(g(x)) and g(f(x)) and...Ch. 2.7 - In Exercises 1-10, find f(g(x)) and g(f(x)) and...Ch. 2.7 - In Exercises 1-10, find f(g(x)) and g(f(x)) and...Ch. 2.7 - In Exercises 1-10, find f(g(x)) and g(f(x)) and...Ch. 2.7 - The functions in Exercises 11-28 are all...Ch. 2.7 - The functions in Exercises 11-28 are all...Ch. 2.7 - The functions in Exercises 11-28 are all...Ch. 2.7 - Prob. 14ECh. 2.7 - Prob. 15ECh. 2.7 - Prob. 16ECh. 2.7 - The functions in Exercises 11-28 are all...Ch. 2.7 - Prob. 18ECh. 2.7 - Prob. 19ECh. 2.7 - Prob. 20ECh. 2.7 - The functions in Exercises 11-28 are all...Ch. 2.7 - Prob. 22ECh. 2.7 - The functions in Exercises 11-28 are all...Ch. 2.7 - Prob. 24ECh. 2.7 - The functions in Exercises 11-28 are all...Ch. 2.7 - Prob. 26ECh. 2.7 - Prob. 27ECh. 2.7 - Prob. 28ECh. 2.7 - Which graphs in Exercises 29-34 represent...Ch. 2.7 - Which graphs in Exercises 29-34 represent...Ch. 2.7 - Which graphs in Exercises 29-34 represent...Ch. 2.7 - Which graphs in Exercises 29-34 represent...Ch. 2.7 - Prob. 33ECh. 2.7 - Which graphs in Exercises 29-34 represent...Ch. 2.7 - In Exercises 35-38, use the graph of f to draw the...Ch. 2.7 - In Exercises 35-38, use the graph of f to draw the...Ch. 2.7 - In Exercises 35-38, use the graph of f to draw the...Ch. 2.7 - Prob. 38ECh. 2.7 - In Exercises 39-52, a. Find an equation for f1(x)....Ch. 2.7 - In Exercises 39-52, a. Find an equation for . b....Ch. 2.7 - In Exercises 39-52, a. Find an equation for f1(x)....Ch. 2.7 - In Exercises 39-52, a. Find an equation for . b....Ch. 2.7 - In Exercises 39-52, a. Find an equation for f1(x)....Ch. 2.7 - Prob. 44ECh. 2.7 - Prob. 45ECh. 2.7 - Prob. 46ECh. 2.7 - Prob. 47ECh. 2.7 - Prob. 48ECh. 2.7 - Prob. 49ECh. 2.7 - Prob. 50ECh. 2.7 - In Exercises 39-52, a. Find an equation for . b....Ch. 2.7 - In Exercises 39-52, a. Find an equation for . b....Ch. 2.7 - In Exercises 53-58, f and g are defined by the...Ch. 2.7 - Prob. 54ECh. 2.7 - In Exercises 53-58, f and g are defined by the...Ch. 2.7 - In Exercises 53-58, f and g are defined by the...Ch. 2.7 - In Exercises 53-58, f and g are defined by the...Ch. 2.7 - Prob. 58ECh. 2.7 - In Exercises 59-64, let Evaluate the indicated...Ch. 2.7 - Prob. 60ECh. 2.7 - Prob. 61ECh. 2.7 - Prob. 62ECh. 2.7 - In Exercises 59-64, let Evaluate the indicated...Ch. 2.7 - f(g[h(1)])Ch. 2.7 - Prob. 65ECh. 2.7 - Prob. 66ECh. 2.7 - Prob. 67ECh. 2.7 - Prob. 68ECh. 2.7 - Prob. 69ECh. 2.7 - Prob. 70ECh. 2.7 - Prob. 71ECh. 2.7 - Prob. 72ECh. 2.7 - Prob. 73ECh. 2.7 - Prob. 74ECh. 2.7 - Prob. 75ECh. 2.7 - Prob. 76ECh. 2.7 - Prob. 77ECh. 2.7 - Prob. 78ECh. 2.7 - Prob. 79ECh. 2.7 - Prob. 80ECh. 2.7 - In Exercises 76-83, use a graphing utility to...Ch. 2.7 - Prob. 82ECh. 2.7 - Prob. 83ECh. 2.7 - Prob. 84ECh. 2.7 - Prob. 85ECh. 2.7 - Prob. 86ECh. 2.7 - Prob. 87ECh. 2.7 - Prob. 88ECh. 2.7 - Prob. 89ECh. 2.7 - Make Sense? In Exercises 87-90 , determine whether...Ch. 2.7 - Prob. 91ECh. 2.7 - Prob. 92ECh. 2.7 - In Exercises 91-94, determine whether each...Ch. 2.7 - Prob. 94ECh. 2.7 - Prob. 95ECh. 2.7 - Prob. 96ECh. 2.7 - Prob. 97ECh. 2.7 - Prob. 98ECh. 2.7 - Prob. 99ECh. 2.7 - Prob. 100ECh. 2.7 - Prob. 101ECh. 2.7 - Prob. 102ECh. 2.7 - Prob. 103ECh. 2.7 - Prob. 104ECh. 2.7 - Exercises 103-105 will help you prepare for the...Ch. 2.8 - Fill in each blank so that the resulting statement...Ch. 2.8 - Fill in each blank so that the resulting statement...Ch. 2.8 - Fill in each blank so that the resulting statement...Ch. 2.8 - Fill in each blank so that the resulting statement...Ch. 2.8 - Prob. 5CVCCh. 2.8 - Prob. 6CVCCh. 2.8 - In Exercises 1-18, find the distance between each...Ch. 2.8 - In Exercises 1-18, find the distance between each...Ch. 2.8 - In Exercises 1-18, find the distance between each...Ch. 2.8 - Prob. 4ECh. 2.8 - In Exercises 1-18, find the distance between each...Ch. 2.8 - Prob. 6ECh. 2.8 - In Exercises 1-18, find the distance between each...Ch. 2.8 - Prob. 8ECh. 2.8 - In Exercises 1-18, find the distance between each...Ch. 2.8 - In Exercises 1-18, find the distance between each...Ch. 2.8 - In Exercises 1-18, find the distance between each...Ch. 2.8 - In Exercises 1-18, find the distance between each...Ch. 2.8 - In Exercises 1-18, find the distance between each...Ch. 2.8 - In Exercises 1-18, find the distance between each...Ch. 2.8 - In Exercises 1-18, find the distance between each...Ch. 2.8 - In Exercises 1-18, find the distance between each...Ch. 2.8 - In Exercises 1-18, find the distance between each...Ch. 2.8 - In Exercises 1-18, find the distance between each...Ch. 2.8 - In Exercises 19-30, find1 the midpoint of each...Ch. 2.8 - Prob. 20ECh. 2.8 - In Exercises i9-30, find die midpoint of each line...Ch. 2.8 - Prob. 22ECh. 2.8 - In Exercises 19-30, find die midpoint of each line...Ch. 2.8 - In Exercises 19-30, find die midpoint of each line...Ch. 2.8 - Prob. 25ECh. 2.8 - In Exercises 19-30, find the midpoint of each Hue...Ch. 2.8 - In Exercises 19-30, find the midpoint of each line...Ch. 2.8 - Prob. 28ECh. 2.8 - In Exercises 19-30, find the midpoint of each line...Ch. 2.8 - In Exercises 19-30, find die midpoint of each line...Ch. 2.8 - Prob. 31ECh. 2.8 - Prob. 32ECh. 2.8 - Prob. 33ECh. 2.8 - Prob. 34ECh. 2.8 - Prob. 35ECh. 2.8 - Prob. 36ECh. 2.8 - Prob. 37ECh. 2.8 - Prob. 38ECh. 2.8 - Prob. 39ECh. 2.8 - Prob. 40ECh. 2.8 - In Exercises 11-52, give the center and radius of...Ch. 2.8 - Prob. 42ECh. 2.8 - In Exercises 11-52, given the center and radius of...Ch. 2.8 - In Exercises 11-52, given the center and radius of...Ch. 2.8 - In Exercises 11-52, given the center and radius of...Ch. 2.8 - In Exercises 11-52, give the center and radius of...Ch. 2.8 - In Exercises 11-52, give the center and radius of...Ch. 2.8 - In Exercises 11-52, give the center and radius of...Ch. 2.8 - In Exercises 11-52, given the center and radium of...Ch. 2.8 - In Exercises 11-52, given the center and radius of...Ch. 2.8 - Prob. 51ECh. 2.8 - In Exercises 11-52, give the center and radius of...Ch. 2.8 - In Exercises 53-64, complete the square and write...Ch. 2.8 - In Exercises 53-64, complete the square and write...Ch. 2.8 - In Exercises 53-64, complete the square and write...Ch. 2.8 - In Exercises 53-64, complete the square and write...Ch. 2.8 - In Exercises 53-64, complete the square and write...Ch. 2.8 - In Exercises 53-64, complete the square and write...Ch. 2.8 - In Exercises 53-64, complete the square and write...Ch. 2.8 - In Exercises 53-64, complete the square and write...Ch. 2.8 - In Exercises 53-64, complete the square and write...Ch. 2.8 - In Exercises 53-64, complete the square and write...Ch. 2.8 - In Exercises 53-64, complete the square and write...Ch. 2.8 - In Exercises 53-64, complete the square and write...Ch. 2.8 - In Exercises 65-66, a line segment through the...Ch. 2.8 - Prob. 66ECh. 2.8 - Prob. 67ECh. 2.8 - Prob. 68ECh. 2.8 - Prob. 69ECh. 2.8 - Prob. 70ECh. 2.8 - Prob. 71ECh. 2.8 - Prob. 72ECh. 2.8 - A rectangular coordinate system with coordinate in...Ch. 2.8 - Prob. 74ECh. 2.8 - Prob. 75ECh. 2.8 - Prob. 76ECh. 2.8 - Prob. 77ECh. 2.8 - Prob. 78ECh. 2.8 - Prob. 79ECh. 2.8 - Prob. 80ECh. 2.8 - Prob. 81ECh. 2.8 - Prob. 82ECh. 2.8 - Prob. 83ECh. 2.8 - Prob. 84ECh. 2.8 - Prob. 85ECh. 2.8 - Make Sense? In Exercises 86-89, determine whether...Ch. 2.8 - Prob. 87ECh. 2.8 - Prob. 88ECh. 2.8 - Prob. 89ECh. 2.8 - Prob. 90ECh. 2.8 - Prob. 91ECh. 2.8 - In Exercises 90-9, determine whether each...Ch. 2.8 - In Exercises 90-93, determine whether each...Ch. 2.8 - Prob. 94ECh. 2.8 - Prob. 95ECh. 2.8 - Prob. 96ECh. 2.8 - Prob. 97ECh. 2.8 - Prob. 98ECh. 2.8 - Prob. 99ECh. 2.8 - Prob. 100ECh. 2.8 - Prob. 101ECh. 2.8 - Prob. 102ECh. 2.8 - Exercises 101-103 will help yon prepare for the...Ch. 2 - In Exercises 1-6, determine whether each relation...Ch. 2 - In Exercises 1-6, determine whether each relation...Ch. 2 - In Exercises 1-6, determine whether each relation...Ch. 2 - In Exercises 1-6, determine whether each relation...Ch. 2 - In Exercises 1-6, determine whether each relation...Ch. 2 - In Exercises 1-6, determine whether each relation...Ch. 2 - In Exercises IS, determine whether each equation...Ch. 2 - In Exercises 7-8, determine whether each equation...Ch. 2 - In Exercises 1-6, determine whether each relation...Ch. 2 - Use the graph of f to solve Exercises 9-24. Where...Ch. 2 - Use the graph of f to solve Exercises 9-24, Where...Ch. 2 - Use the graph of f solve Exercises 9-24, Where...Ch. 2 - Use the graph of f to solve Exercises 9-24 Where...Ch. 2 - Use the graph of f to solve Exercises 9-24. Where...Ch. 2 - Use the graph of f to solve Exercises 9-24. Where...Ch. 2 - Use the graph of f to solve Exercises 9-24. Where...Ch. 2 - Use the graph of f to solve Exercises 9-24. Where...Ch. 2 - Use the graph of f to solve Exercises 9-24. Where...Ch. 2 - Use the graph of f to solve Exercises 9-24. Where...Ch. 2 - Use the graph of f to solve Exercises 9-24. Where...Ch. 2 - Use the graph of f to solve Exercises 9-24. Where...Ch. 2 - Use the graph of f to solve Exercises 9-24. Where...Ch. 2 - Use the graph of f to solve Exercises 9-24. Where...Ch. 2 - Use the graph of f solve Exercises 9-24. Where...Ch. 2 - In Exercises 25-26, determine whether the graph of...Ch. 2 - In Exercises 25-26, determine whether the graph of...Ch. 2 - In Exercises 27-38, graph each equation in a...Ch. 2 - In Exercises 27-38, graph each equation in a...Ch. 2 - In Exercises 27-38, graph each equation in a...Ch. 2 - In Exercises 27-38, graph each equation in a...Ch. 2 - In Exercises 27-38, graph each equation in a...Ch. 2 - In Exercises 27-38, graph each equation in a...Ch. 2 - In Exercises 27-38, graph each equation in a...Ch. 2 - In Exercises 27-38, graph each equation in a...Ch. 2 - In Exercises 27-38, graph each equation in a...Ch. 2 - In Exercises 27-38, graph each equation in a...Ch. 2 - In Exercises 27-38, graph each equation in a...Ch. 2 - In Exercises 27-38, graph each equation in a...Ch. 2 - 39. Let a. Find . Is f even, odd, or...Ch. 2 - 40. Let a. Find C (150). b. Find C (250). Ch. 2 - In Exercises 41-44, write a function in...Ch. 2 - In Exercises 41-44, write a function in...Ch. 2 - In Exercises 41-44, write a function in...Ch. 2 - In Exercises 41-44, write a function in...Ch. 2 - 45. Determine whether the line through and (7, 0)...Ch. 2 - Exercise is useful not only in preventing...Ch. 2 - 47. Find the average raw of change of from to . Ch. 2 - In Exercises 1-3, determine whether each relation...Ch. 2 - In Exercises 1-3, determine whether each relation...Ch. 2 - In Exercises 1-3, determine whether each relation...Ch. 2 - In Exercises 4-6, determine whether each equation...Ch. 2 - In Exercise 4-6, determine whether each equation...Ch. 2 - In Exercises 4-6, determine whether each equation...Ch. 2 - In Exercises 7-10, evaluate each function at the...Ch. 2 - In Exercises 7-10, evaluate each function at the...Ch. 2 - In Exercises 7-10, evaluate each function at the...Ch. 2 - In Exercises 7-10, evaluate each function at the...Ch. 2 - Prob. 11RECh. 2 - In Exercises 11-16, use the vertical line test to...Ch. 2 - In Exercise 11-16, use (he vertical line test to...Ch. 2 - In Exercises 11-I6, use the vertical line test to...Ch. 2 - In Exercises 11-16, use Hue vertical line ten to...Ch. 2 - In Exercises 11-16, use the vertical line test to...Ch. 2 - Prob. 17RECh. 2 - Prob. 18RECh. 2 - Prob. 19RECh. 2 - Prob. 20RECh. 2 - Prob. 21RECh. 2 - In Exercises 22 -24 , determine whether the graph...Ch. 2 - In Exercises 22 -24 , determine whether the graph...Ch. 2 - In Exercises 22-24, determine whether the graph of...Ch. 2 - In Exercises 25 27, determine whether each graph u...Ch. 2 - In Exercises 25-27, determine whether each graph...Ch. 2 - In Exercises 25 27, determine whether each graph...Ch. 2 - In Exercises 28-30, determine whether each...Ch. 2 - In Exercises 28-30, determine whether each...Ch. 2 - In Exercises 28 -30 . determine whether each...Ch. 2 - In Exercises 31-32, the domain of each pieceivise...Ch. 2 - In Exercises 31-32, the domain of each piecewise...Ch. 2 - In Exercises 33-34, find and simplify the...Ch. 2 - Prob. 34RECh. 2 - The graph shows the height, in meters, of an eagle...Ch. 2 - Prob. 36RECh. 2 - Prob. 37RECh. 2 - Prob. 38RECh. 2 - Prob. 39RECh. 2 - Prob. 40RECh. 2 - Prob. 41RECh. 2 - Prob. 42RECh. 2 - In Exercises 41-44, use the given conditions to...Ch. 2 - Prob. 44RECh. 2 - Prob. 45RECh. 2 - Prob. 46RECh. 2 - Prob. 47RECh. 2 - Prob. 48RECh. 2 - Prob. 49RECh. 2 - Prob. 50RECh. 2 - Prob. 51RECh. 2 - 52. The bar graph shows the average age at which...Ch. 2 - Prob. 53RECh. 2 - Prob. 54RECh. 2 - Prob. 55RECh. 2 - In Exercises 55-59, use the graph of y=f(x) to...Ch. 2 - In Exercises 55-59, use the graph of y=f(x) to...Ch. 2 - Prob. 58RECh. 2 - In Exercises 55-59, use the graph of y=f(x) to...Ch. 2 - Prob. 60RECh. 2 - In Exercises 60-63, begin by graphing the standard...Ch. 2 - In Exercises 60-63, begin by graphing the standard...Ch. 2 - In Exercises 60-63, begin by graphing the standard...Ch. 2 - In Exercises 64-66, begin by graphing the square...Ch. 2 - In Exercises 60-63, begin by graphing the standard...Ch. 2 - In Exercises 60-63, begin by graphing the standard...Ch. 2 - In Exercises 67-69, begin by graphing the absolute...Ch. 2 - In Exercises 67-69, begin by graphing the absolute...Ch. 2 - In Exercises 67-69, begin by graphing the absolute...Ch. 2 - In Exercises 70-72, begin by graphing the standard...Ch. 2 - In Exercises 70-72, begin by graphing the standard...Ch. 2 - In Exercises 70-72, begin by graphing the standard...Ch. 2 - In Exercises 73-75, begin by graphing the cube...Ch. 2 - In Exercises 73-75, begin by graphing the cube...Ch. 2 - In Exercises 73-75, begin by graphing the cube...Ch. 2 - In Exercises 76-81, find the domain of each...Ch. 2 - In Exercises 76-81, find /he domain of each...Ch. 2 - In Exercises 76-81, find the domain of each...Ch. 2 - In Exercises 76-81, find the domain of each...Ch. 2 - In Exercises 76-81, find the domain of each...Ch. 2 - In Exercises 76-81, find the domain of each...Ch. 2 - In Exercises 82-84, find , and Determine the...Ch. 2 - In Exercises 82-84, find f+g,fg,fg , and 1g...Ch. 2 - In Exercises 82-84, find f+g,fg,fg , and 1g...Ch. 2 - In Exercises 05-86, find a. b. c. 85. Ch. 2 - In Exercises 05-86, find a. (fg)(x); b. (gf)(x);...Ch. 2 - In Exercises 87-88, find a. (fg)(x); b, the domain...Ch. 2 - In Exercises 87-88, find a. (fg)(x); b. the domain...Ch. 2 - In Exercises 89-90, express the given function h...Ch. 2 - In Exercises 89-90, express the given function h...Ch. 2 - In Exercises 91-9Z find f(g (x)) and g(f(x)) and...Ch. 2 - In Exercises 91-93 find f(g (x)) and g(f(x)) and...Ch. 2 - The functions in Exercises 93-95 tire tilt...Ch. 2 - The functions in Exercises 93-95 tire tilt...Ch. 2 - The functions in Exercises 93-95 tire tilt...Ch. 2 - Which graphs in Exercises 96-99 represent function...Ch. 2 - Which graphs in Exercises 96-99, represent...Ch. 2 - Which graphs in Exercises 96-99, represent...Ch. 2 - Which graphs in Exercises 96-99 represent function...Ch. 2 - 100. Use the graph of f in the figure shown to...Ch. 2 - Prob. 101RECh. 2 - Prob. 102RECh. 2 - Prob. 103RECh. 2 - Prob. 104RECh. 2 - Prob. 105RECh. 2 - Prob. 106RECh. 2 - Prob. 107RECh. 2 - Prob. 108RECh. 2 - Prob. 109RECh. 2 - Prob. 110RECh. 2 - Prob. 111RECh. 2 - Prob. 1TCh. 2 - Prob. 2TCh. 2 - Prob. 3TCh. 2 - In Exercises 4-15, graph each Equation m a...Ch. 2 - In Exercises 4-15, graph each equation in a...Ch. 2 - Prob. 6TCh. 2 - Prob. 7TCh. 2 - Prob. 8TCh. 2 - Prob. 9TCh. 2 - Prob. 10TCh. 2 - Prob. 11TCh. 2 - Prob. 12TCh. 2 - Prob. 13TCh. 2 - Prob. 14TCh. 2 - Prob. 15TCh. 2 - Prob. 16TCh. 2 - Prob. 17TCh. 2 - Prob. 18TCh. 2 - Prob. 19TCh. 2 - Prob. 20TCh. 2 - Prob. 21TCh. 2 - Prob. 22TCh. 2 - Prob. 23TCh. 2 - Prob. 24TCh. 2 - Prob. 25TCh. 2 - Prob. 26TCh. 2 - Prob. 27TCh. 2 - Prob. 28TCh. 2 - Prob. 29TCh. 2 - Prob. 30TCh. 2 - Prob. 31TCh. 2 - Prob. 32TCh. 2 - Prob. 33TCh. 2 - Prob. 34TCh. 2 - Prob. 35TCh. 2 - Prob. 1CRECh. 2 - Prob. 2CRECh. 2 - Prob. 3CRECh. 2 - Prob. 4CRECh. 2 - Prob. 5CRECh. 2 - Prob. 6CRECh. 2 - In Exercises 6-1, solve each equation or...Ch. 2 - In Exercises 6-10, solve each equation or...Ch. 2 - In Exercises 6-10, solve each equation or...Ch. 2 - In Exercise 6-10, solve each equation or...Ch. 2 - In Exercises I1-14, graph each equation in u...Ch. 2 - In Exercises I l-N, graph each equation in u...Ch. 2 - In Exercises I1-14, graph each equation in u...Ch. 2 - In Exercises 11-94, graph each equation in u...Ch. 2 - In Exercises 15-16, let and 15. Find and...Ch. 2 - In Exercises 15-16, let f(x) and 16. Find all...Ch. 2 - 17. Write equations in point-slope form,...Ch. 2 - You invested $6000 in two accounts paying 7% and...Ch. 2 - Fur a summer sales job, you are choosing between...Ch. 2 - 20. The length of a rectangular garden is 2 feel...
Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Recommended textbooks for you
Text book image
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Text book image
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Text book image
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Text book image
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Correlation Vs Regression: Difference Between them with definition & Comparison Chart; Author: Key Differences;https://www.youtube.com/watch?v=Ou2QGSJVd0U;License: Standard YouTube License, CC-BY
Correlation and Regression: Concepts with Illustrative examples; Author: LEARN & APPLY : Lean and Six Sigma;https://www.youtube.com/watch?v=xTpHD5WLuoA;License: Standard YouTube License, CC-BY