University Calculus, Early Transcendentals, Single Variable Plus MyLab Math -- Access Card Package (3rd Edition)
3rd Edition
ISBN: 9780321999597
Author: Joel R. Hass, Maurice D. Weir
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 2.3, Problem 57E
To determine
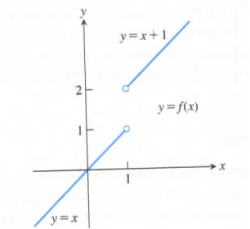
To Prove: Refer to the given figure, show that
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Under certain conditions, the number of diseased cells N(t) at time t increases at a rate N'(t) = Aekt, where A is the rate of increase at time 0 (in cells per day) and k is a constant.
(a) Suppose A = 60, and at 3 days, the cells are growing at a rate of 180 per day. Find a formula for the number of cells after t days, given that 200 cells are present at t = 0.
(b) Use your answer from part (a) to find the number of cells present after 8 days.
(a) Find a formula for the number of cells, N(t), after t days.
N(t) =
(Round any numbers in exponents to five decimal places. Round all other numbers to the nearest tenth.)
The marginal revenue (in thousands of dollars) from the sale of x handheld gaming devices is given by the following function.
R'(x) = 4x (x² +26,000)
2
3
(a) Find the total revenue function if the revenue from 125 devices is $17,939.
(b) How many devices must be sold for a revenue of at least $50,000?
(a) The total revenue function is R(x) =
(Round to the nearest integer as needed.)
given that the revenue from 125 devices is $17,939.
Use substitution to find the indefinite integral.
S
2u
√u-4
-du
Describe the most appropriate substitution case and the values of u and du. Select the correct choice below and fill in the answer boxes within your choice.
A. Substitute u for the quantity in the numerator. Let v =
, so that dv = ( ) du.
B. Substitute u for the quantity under the root. Let v = u-4, so that dv = (1) du.
C. Substitute u for the quantity in the denominator. Let v =
Use the substitution to evaluate the integral.
so that dv=
'
(
du.
2u
-du=
√√u-4
Chapter 2 Solutions
University Calculus, Early Transcendentals, Single Variable Plus MyLab Math -- Access Card Package (3rd Edition)
Ch. 2.1 - In Exercises 1-6, find the average rate of change...Ch. 2.1 - Prob. 2ECh. 2.1 - In Exercises 1-6, find the average rate of change...Ch. 2.1 - Prob. 4ECh. 2.1 - Prob. 5ECh. 2.1 - Prob. 6ECh. 2.1 - Prob. 7ECh. 2.1 - Prob. 8ECh. 2.1 - Prob. 9ECh. 2.1 - Prob. 10E
Ch. 2.1 - Prob. 11ECh. 2.1 - In Exercises 7-18, use the method in Example 3 to...Ch. 2.1 - Prob. 13ECh. 2.1 - Prob. 14ECh. 2.1 - Prob. 15ECh. 2.1 - Prob. 16ECh. 2.1 - The profits of a small company for each of the...Ch. 2.1 - Make a table of values for the function...Ch. 2.1 - 25. The accompanying graph shows the total...Ch. 2.1 - The accompanying graph shows the total amount of...Ch. 2.2 - For the function graphed here, find the following...Ch. 2.2 - Prob. 2ECh. 2.2 - Prob. 5ECh. 2.2 - Prob. 6ECh. 2.2 - Prob. 7ECh. 2.2 - 8. Suppose that a function is defined for all...Ch. 2.2 - Prob. 9ECh. 2.2 - Prob. 10ECh. 2.2 - Prob. 11ECh. 2.2 - Prob. 12ECh. 2.2 - Prob. 13ECh. 2.2 - Prob. 14ECh. 2.2 - Prob. 15ECh. 2.2 - Prob. 16ECh. 2.2 - Prob. 17ECh. 2.2 - Prob. 18ECh. 2.2 - Prob. 19ECh. 2.2 - Prob. 20ECh. 2.2 - Prob. 21ECh. 2.2 - Find the limits in Exercises 11-22.
22.
Ch. 2.2 - Prob. 23ECh. 2.2 - Prob. 24ECh. 2.2 - Prob. 25ECh. 2.2 - Prob. 26ECh. 2.2 - Prob. 27ECh. 2.2 - Prob. 28ECh. 2.2 - Prob. 29ECh. 2.2 - Prob. 30ECh. 2.2 - Prob. 31ECh. 2.2 - Prob. 32ECh. 2.2 - Prob. 33ECh. 2.2 - Prob. 34ECh. 2.2 - Prob. 35ECh. 2.2 - Prob. 36ECh. 2.2 - Prob. 37ECh. 2.2 - Prob. 38ECh. 2.2 - Prob. 39ECh. 2.2 - Prob. 40ECh. 2.2 - Prob. 41ECh. 2.2 - Prob. 42ECh. 2.2 - Prob. 43ECh. 2.2 - Prob. 45ECh. 2.2 - Prob. 47ECh. 2.2 - Prob. 48ECh. 2.2 - Prob. 49ECh. 2.2 - Prob. 50ECh. 2.2 - Prob. 52ECh. 2.2 - Prob. 53ECh. 2.2 - Prob. 54ECh. 2.2 - Prob. 55ECh. 2.2 - Prob. 56ECh. 2.2 - Prob. 57ECh. 2.2 - Prob. 58ECh. 2.2 - Prob. 59ECh. 2.2 - Prob. 60ECh. 2.2 - Prob. 61ECh. 2.2 - Prob. 62ECh. 2.2 - 63. If for , find .
Ch. 2.2 - Prob. 64ECh. 2.2 - It can be shown that the inequalities...Ch. 2.2 - Prob. 67ECh. 2.2 - Prob. 68ECh. 2.2 - Prob. 69ECh. 2.2 - Prob. 70ECh. 2.2 - You will find a graphing calculator useful for...Ch. 2.2 - Prob. 72ECh. 2.2 - Prob. 73ECh. 2.2 - Prob. 74ECh. 2.2 - Prob. 75ECh. 2.2 - Prob. 76ECh. 2.2 - Prob. 77ECh. 2.2 - Prob. 78ECh. 2.2 - Prob. 79ECh. 2.2 - Prob. 80ECh. 2.2 - Prob. 81ECh. 2.2 - Prob. 82ECh. 2.2 - Prob. 83ECh. 2.2 - Prob. 84ECh. 2.2 - Prob. 85ECh. 2.2 - Prob. 86ECh. 2.2 - COMPUTER EXPLORATIONS Graphical Estimates of...Ch. 2.2 - Prob. 88ECh. 2.2 - Prob. 89ECh. 2.2 - Prob. 90ECh. 2.3 - Prob. 1ECh. 2.3 - Prob. 2ECh. 2.3 - Prob. 3ECh. 2.3 - Prob. 4ECh. 2.3 - Prob. 5ECh. 2.3 - Prob. 6ECh. 2.3 - Prob. 7ECh. 2.3 - Prob. 8ECh. 2.3 - Prob. 9ECh. 2.3 - Prob. 10ECh. 2.3 - Prob. 11ECh. 2.3 - Prob. 12ECh. 2.3 - Prob. 13ECh. 2.3 - Prob. 14ECh. 2.3 - Prob. 15ECh. 2.3 - Prob. 16ECh. 2.3 - Prob. 17ECh. 2.3 - Prob. 18ECh. 2.3 - Prob. 19ECh. 2.3 - Prob. 20ECh. 2.3 - Prob. 21ECh. 2.3 - Finding Deltas Algebraically
Each of Exercises...Ch. 2.3 - Prob. 23ECh. 2.3 - Prob. 24ECh. 2.3 - Prob. 25ECh. 2.3 - Prob. 26ECh. 2.3 - Prob. 27ECh. 2.3 - Prob. 28ECh. 2.3 - Prob. 29ECh. 2.3 - Prob. 30ECh. 2.3 - Prob. 31ECh. 2.3 - Prob. 32ECh. 2.3 - Prob. 33ECh. 2.3 - Prob. 34ECh. 2.3 - Prob. 35ECh. 2.3 - Prob. 36ECh. 2.3 - Prob. 37ECh. 2.3 - Prob. 38ECh. 2.3 - Prob. 39ECh. 2.3 - Prob. 40ECh. 2.3 - Prob. 41ECh. 2.3 - Prob. 42ECh. 2.3 - Prob. 43ECh. 2.3 - Prob. 45ECh. 2.3 - Prob. 46ECh. 2.3 - Prob. 47ECh. 2.3 - Prove the limit statements in exercises 37-50....Ch. 2.3 - Prob. 49ECh. 2.3 - Prob. 50ECh. 2.3 - Prob. 51ECh. 2.3 - Prob. 52ECh. 2.3 - Prob. 53ECh. 2.3 - Theory and Examples Another wrong statement about...Ch. 2.3 - Prob. 55ECh. 2.3 - Prob. 56ECh. 2.3 - Prob. 57ECh. 2.3 - Prob. 58ECh. 2.3 - Prob. 59ECh. 2.3 - Prob. 60ECh. 2.3 - Prob. 61ECh. 2.3 - COMPUTER EXPLORATIONS
In Exercises 61-66, you will...Ch. 2.3 - Prob. 63ECh. 2.3 - Prob. 64ECh. 2.3 - COMPUTER EXPLORATIONS In Exercises 61-66, you will...Ch. 2.3 - Prob. 66ECh. 2.4 - Finding Limits Graphically Which of the following...Ch. 2.4 - Finding Limits Graphically Which of the following...Ch. 2.4 - 3. Let
a. Find and .
b. Does exist? If so,...Ch. 2.4 - Let f(x)={x2,x2.3x,x22,x=2 Find limx2+f(x),...Ch. 2.4 - 5. Let
a. Does exist? If so, what is it? If...Ch. 2.4 - 6. Let
a. Does exist? If so, what is it? If...Ch. 2.4 - Graph f(x)={0,x=1.x3,x1 Find limx1f(x) and...Ch. 2.4 - Graph f(x)={2,x=1.1x2,x1 Find limx1+f(x) and...Ch. 2.4 - Graph the functions In Exercises 9 and 10. Then...Ch. 2.4 - Graph the functions In Exercises 9 and 10. Then...Ch. 2.4 - Finding One-Sided Limits Algebraically Find the...Ch. 2.4 - Finding One-Sided Limits Algebraically Find the...Ch. 2.4 - Finding One-Sided Limits Algebraically Find the...Ch. 2.4 - Finding One-Sided Limits Algebraically Find the...Ch. 2.4 - Finding One-Sided Limits Algebraically
Find the...Ch. 2.4 - Finding One-Sided Limits Algebraically
Find the...Ch. 2.4 - Prob. 17ECh. 2.4 - Finding One-Sided Limits Algebraically Find the...Ch. 2.4 - Use the graph of the greatest integer function ,...Ch. 2.4 - Use the graph of the greatest integer function ,...Ch. 2.4 - Using
Find the limits in Exercises 23-46.
23.
Ch. 2.4 - Using
Find the limits in Exercises 23-46.
24.
Ch. 2.4 - Prob. 23ECh. 2.4 - Using
Find the limits in Exercises 23-46.
26.
Ch. 2.4 - Using limx0sin=1 Find the limits in Exercises...Ch. 2.4 - Using
Find the limits in Exercises 23-46.
28.
Ch. 2.4 - Using
Find the limits in Exercises 23-46.
29.
Ch. 2.4 - Using limx0sin=1 Find the limits in Exercises...Ch. 2.4 - Prob. 29ECh. 2.4 - Using
Find the limits in Exercises 23-46.
32.
Ch. 2.4 - Using
Find the limits in Exercises 23-46.
33.
Ch. 2.4 - Using lim0sin=1 Find the limits in Exercises...Ch. 2.4 - Using
Find the limits in Exercises 23-46.
35.
Ch. 2.4 - Using lim0sin=1 Find the limits in Exercises...Ch. 2.4 - Using lim0sin=1 Find the limits in Exercises...Ch. 2.4 - Using lim0sin=1 Find the limits in Exercises...Ch. 2.4 - Using lim0sin=1 Find the limits in Exercises...Ch. 2.4 - Using
Find the limits in Exercises 23-46.
40.
Ch. 2.4 - Using lim0sin=1 Find the limits in Exercises...Ch. 2.4 - Using
Find the limits in Exercises 23-46.
42.
Ch. 2.4 - Using lim0sin=1 Find the limits in Exercises...Ch. 2.4 - Using
Find the limits in Exercises 23-46.
44.
Ch. 2.4 - Theory and Examples
47. Once you know and at an...Ch. 2.4 - Theory and Examples If you know that limxcf(x)...Ch. 2.4 - Theory and Examples Suppose that f is an odd...Ch. 2.4 - Theory and Examples Suppose that f is an even...Ch. 2.4 - Prob. 47ECh. 2.4 - Prob. 48ECh. 2.4 - Use the definitions of right-hand and left-hand...Ch. 2.4 - Use the definitions of right-hand and left-hand...Ch. 2.4 - 55. Greatest integer function Find (a) and (b) ;...Ch. 2.4 - Prob. 52ECh. 2.5 - Prob. 1ECh. 2.5 - Prob. 2ECh. 2.5 - Prob. 3ECh. 2.5 - Prob. 4ECh. 2.5 - Prob. 5ECh. 2.5 - Prob. 6ECh. 2.5 - Prob. 7ECh. 2.5 - Prob. 8ECh. 2.5 - Prob. 9ECh. 2.5 - Prob. 10ECh. 2.5 - At which points do the functions in Exercises 11...Ch. 2.5 - Prob. 12ECh. 2.5 - Prob. 13ECh. 2.5 - Prob. 14ECh. 2.5 - Prob. 15ECh. 2.5 - Prob. 16ECh. 2.5 - Prob. 17ECh. 2.5 - Prob. 18ECh. 2.5 - Prob. 19ECh. 2.5 - Prob. 20ECh. 2.5 - Prob. 21ECh. 2.5 - Prob. 22ECh. 2.5 - Prob. 23ECh. 2.5 - Prob. 24ECh. 2.5 - Prob. 25ECh. 2.5 - Prob. 26ECh. 2.5 - Prob. 27ECh. 2.5 - Prob. 28ECh. 2.5 - Prob. 29ECh. 2.5 - Prob. 30ECh. 2.5 - Prob. 31ECh. 2.5 - Prob. 32ECh. 2.5 - Prob. 33ECh. 2.5 - Prob. 34ECh. 2.5 - Prob. 35ECh. 2.5 - Prob. 36ECh. 2.5 - Find the limits in Exercises 33-40. Are the...Ch. 2.5 - Find the limits in Exercises 33-40. Are the...Ch. 2.5 - Prob. 39ECh. 2.5 - Prob. 40ECh. 2.5 - Prob. 41ECh. 2.5 - Prob. 42ECh. 2.5 - Prob. 43ECh. 2.5 - Prob. 44ECh. 2.5 - Prob. 45ECh. 2.5 - Prob. 47ECh. 2.5 - Prob. 48ECh. 2.5 - Prob. 49ECh. 2.5 - Prob. 50ECh. 2.5 - Prob. 51ECh. 2.5 - Prob. 52ECh. 2.5 - Prob. 53ECh. 2.5 - Prob. 54ECh. 2.5 - Prob. 55ECh. 2.5 - Prob. 56ECh. 2.5 - Prob. 57ECh. 2.5 - Prob. 58ECh. 2.5 - Prob. 59ECh. 2.5 - Prob. 60ECh. 2.5 - Prob. 61ECh. 2.5 - Prob. 62ECh. 2.5 - Prob. 63ECh. 2.5 - Prob. 64ECh. 2.5 - Prob. 65ECh. 2.5 - Stretching a rubber band Is it true that if you...Ch. 2.5 - Prob. 67ECh. 2.5 - Prob. 68ECh. 2.5 - Prove that f is continuous at c if and only if...Ch. 2.5 - Prob. 70ECh. 2.5 - Prob. 71ECh. 2.5 - Prob. 72ECh. 2.5 - Prob. 73ECh. 2.5 - Prob. 74ECh. 2.5 - Prob. 75ECh. 2.5 - Prob. 76ECh. 2.5 - Prob. 77ECh. 2.5 - T Use the Intermediate Value Theorem in Exercises...Ch. 2.6 - For the function f whose graph is given, determine...Ch. 2.6 - For the function whose graph is given, determine...Ch. 2.6 - Prob. 3ECh. 2.6 - Prob. 4ECh. 2.6 - Prob. 5ECh. 2.6 - Prob. 6ECh. 2.6 - Prob. 7ECh. 2.6 - Prob. 8ECh. 2.6 - Prob. 9ECh. 2.6 - Find the limits in Exercises 9-12
10.
Ch. 2.6 - Prob. 11ECh. 2.6 - Prob. 12ECh. 2.6 - Prob. 13ECh. 2.6 - Prob. 14ECh. 2.6 - Prob. 15ECh. 2.6 - Prob. 16ECh. 2.6 - Prob. 17ECh. 2.6 - Prob. 18ECh. 2.6 - Prob. 19ECh. 2.6 - Prob. 20ECh. 2.6 - Prob. 21ECh. 2.6 - Prob. 22ECh. 2.6 - Prob. 23ECh. 2.6 - Prob. 24ECh. 2.6 - Prob. 25ECh. 2.6 - Prob. 26ECh. 2.6 - Prob. 27ECh. 2.6 - Prob. 28ECh. 2.6 - The process by which we determine limits of...Ch. 2.6 - Prob. 30ECh. 2.6 - Prob. 31ECh. 2.6 - Prob. 32ECh. 2.6 - Prob. 33ECh. 2.6 - Prob. 34ECh. 2.6 - Prob. 35ECh. 2.6 - Prob. 36ECh. 2.6 - Prob. 37ECh. 2.6 - Prob. 38ECh. 2.6 - Prob. 39ECh. 2.6 - Prob. 40ECh. 2.6 - Prob. 41ECh. 2.6 - Prob. 42ECh. 2.6 - Prob. 43ECh. 2.6 - Prob. 44ECh. 2.6 - Prob. 45ECh. 2.6 - Prob. 46ECh. 2.6 - Prob. 47ECh. 2.6 - Prob. 48ECh. 2.6 - Prob. 49ECh. 2.6 - Prob. 50ECh. 2.6 - Prob. 51ECh. 2.6 - Prob. 52ECh. 2.6 - Prob. 53ECh. 2.6 - Prob. 54ECh. 2.6 - Prob. 55ECh. 2.6 - Prob. 56ECh. 2.6 - Prob. 57ECh. 2.6 - Prob. 58ECh. 2.6 - Prob. 59ECh. 2.6 - Prob. 60ECh. 2.6 - Prob. 61ECh. 2.6 - Prob. 62ECh. 2.6 - Prob. 63ECh. 2.6 - Prob. 64ECh. 2.6 - Graph the rational functions is Exercises 63-68....Ch. 2.6 - Graph the rational functions is Exercises 63-68....Ch. 2.6 - Graph the rational functions is Exercises 63-68....Ch. 2.6 - Graph the rational functions is Exercises 63-68....Ch. 2.6 - In Exercises 75-78, sketch the graph of a function...Ch. 2.6 - In Exercises 75-78, sketch the graph of a function...Ch. 2.6 - In Exercises 75-78, sketch the graph of a function...Ch. 2.6 - In Exercises 75-78, sketch the graph of a function...Ch. 2.6 - In Exercises 79-82, find a function that satisfies...Ch. 2.6 - In Exercises 79-82, find a function that satisfies...Ch. 2.6 - In Exercises 79-82, find a function that satisfies...Ch. 2.6 - In Exercises 79-82, find a function that satisfies...Ch. 2.6 - 83. Suppose that and are polynomials in and...Ch. 2.6 - Suppose that f(x) and g(x) are polynomials in x....Ch. 2.6 - 85. How many horizontal asymptotes can the graph...Ch. 2.6 - Find the limits in Exercises 86-92. (Hint: Try...Ch. 2.6 - Find the limits in Exercises 86-92. (Hint: Try...Ch. 2.6 - Find the limits in Exercises 86-92. (Hint: Try...Ch. 2.6 - Find the limits in Exercises 86-92. (Hint: Try...Ch. 2.6 - Find the limits in Exercises 86-92. (Hint: Try...Ch. 2.6 - Find the limits in Exercises 86-92. (Hint: Try...Ch. 2.6 - Find the limits in Exercises 86-92. (Hint: Try...Ch. 2.6 - Use the formal definitions of limits as to...Ch. 2.6 - Use the formal definitions of limits as x to...Ch. 2.6 - Use formal definitions to prove the limit...Ch. 2.6 - Use formal definitions to prove the limit...Ch. 2.6 - Use formal definitions to prove the limit...Ch. 2.6 - Use formal definitions to prove the limit...Ch. 2.6 - Here is the definition of infinite right-hand...Ch. 2.6 - Use the formal definitions from Exercise 99 to...Ch. 2.6 - Use the formal definitions from Exercise 99 to...Ch. 2.6 - Use the formal definitions from Exercise 99 to...Ch. 2.6 - Use the formal definitions from Exercise 99 to...Ch. 2.6 - Use the formal definitions from Exercise 99 to...Ch. 2.6 - Graph the rational functions in Exercises 105-110....Ch. 2.6 - Graph the rational functions in Exercises 105-110....Ch. 2.6 - Graph the rational functions in Exercises 105-110....Ch. 2.6 - Graph the rational functions in Exercises 105-110....Ch. 2.6 - Graph the rational functions in Exercises 105-110....Ch. 2.6 - Graph the rational functions in Exercises 105-110....Ch. 2.6 - T Graph the curves in Exercises 111-114. Explain...Ch. 2.6 - T Graph the curves in Exercises 111-114. Explain...Ch. 2.6 - T Graph the curves in Exercises 111-114. Explain...Ch. 2.6 - T Graph the curves in Exercises 111-114. Explain...Ch. 2.6 - Prob. 109ECh. 2.6 - Prob. 110ECh. 2 - Prob. 1GYRCh. 2 - Prob. 2GYRCh. 2 - Prob. 3GYRCh. 2 - Question to guide your review Does the existence...Ch. 2 - Prob. 5GYRCh. 2 - Prob. 6GYRCh. 2 - Prob. 7GYRCh. 2 - Prob. 8GYRCh. 2 - Question to guide your review. what exactly does...Ch. 2 - Prob. 10GYRCh. 2 - Prob. 11GYRCh. 2 - Prob. 12GYRCh. 2 - Prob. 13GYRCh. 2 - Questions to guide your review What does it mean...Ch. 2 - 15. What are the basic types of discontinuity?...Ch. 2 - Question to guide your review What does it mean...Ch. 2 - Prob. 17GYRCh. 2 - Prob. 18GYRCh. 2 - Prob. 19GYRCh. 2 - Prob. 20GYRCh. 2 - Question to guide your review What are horizontal...Ch. 2 - Prob. 1PECh. 2 - Prob. 2PECh. 2 - Prob. 3PECh. 2 - Prob. 4PECh. 2 - Prob. 5PECh. 2 - Prob. 6PECh. 2 - Prob. 7PECh. 2 - Prob. 8PECh. 2 - Finding Limits
In exercises 9-28, find the limit...Ch. 2 - Prob. 10PECh. 2 - Prob. 11PECh. 2 - Prob. 12PECh. 2 - Prob. 13PECh. 2 - Prob. 14PECh. 2 - Prob. 15PECh. 2 - Prob. 16PECh. 2 - Prob. 17PECh. 2 - Prob. 18PECh. 2 - Prob. 19PECh. 2 - Prob. 20PECh. 2 - Prob. 21PECh. 2 - Prob. 22PECh. 2 - Prob. 23PECh. 2 - Prob. 24PECh. 2 - Prob. 25PECh. 2 - Prob. 26PECh. 2 - Prob. 27PECh. 2 - Prob. 28PECh. 2 - Prob. 29PECh. 2 - Prob. 30PECh. 2 - Prob. 31PECh. 2 - Prob. 32PECh. 2 - Prob. 33PECh. 2 - T Let f()=32+2. Use the Intermediate Value Theorem...Ch. 2 - Prob. 35PECh. 2 - Prob. 36PECh. 2 - Prob. 37PECh. 2 - Prob. 38PECh. 2 - Prob. 39PECh. 2 - Prob. 40PECh. 2 - Prob. 41PECh. 2 - Prob. 42PECh. 2 - Prob. 43PECh. 2 - Prob. 44PECh. 2 - Prob. 45PECh. 2 - Prob. 46PECh. 2 - Prob. 47PECh. 2 - Prob. 48PECh. 2 - Prob. 49PECh. 2 - Prob. 50PECh. 2 - Prob. 51PECh. 2 - Prob. 52PECh. 2 - Prob. 53PECh. 2 - Prob. 54PECh. 2 - Prob. 55PECh. 2 - Horizontal and vertical asymptotes.
56. Use limits...Ch. 2 - Prob. 1AAECh. 2 - Prob. 2AAECh. 2 - Prob. 3AAECh. 2 - Prob. 4AAECh. 2 - Prob. 5AAECh. 2 - 6. Strips on a measuring cup The interior of a...Ch. 2 - Prob. 7AAECh. 2 - Prob. 8AAECh. 2 - Prob. 9AAECh. 2 - Prob. 10AAECh. 2 - Prob. 11AAECh. 2 - Prob. 12AAECh. 2 - Prob. 13AAECh. 2 - Prob. 14AAECh. 2 - In Exercises 15 and 16, use the formal definition...Ch. 2 - In Exercises 15 and 16, use the formal definition...Ch. 2 - 17. A function continuous at only one point Let
...Ch. 2 - The Dirichlet ruler function If x is a rational...Ch. 2 - 19. Antipodal points Is there any reason to...Ch. 2 - Prob. 20AAECh. 2 - Prob. 21AAECh. 2 - Prob. 22AAECh. 2 - Prob. 23AAECh. 2 - Prob. 25AAECh. 2 - Prob. 26AAECh. 2 - Prob. 27AAECh. 2 - Prob. 28AAECh. 2 - Prob. 29AAECh. 2 - Prob. 30AAECh. 2 - Prob. 31AAECh. 2 - Prob. 32AAECh. 2 - Prob. 33AAECh. 2 - Prob. 34AAE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Use substitution to find the indefinite integral. Зи u-8 du Describe the most appropriate substitution case and the values of u and du. Select the correct choice below and fill in the answer boxes within your choice. A. Substitute u for the quantity in the numerator. Let v = , so that dv = ( ( ) du. B. Substitute u for the quantity under the root. Let v = u-8, so that dv = (1) du. C. Substitute u for the quantity in the denominator. Let v = so that dv= ( ) du. Use the substitution to evaluate the integral. S Зи -du= u-8arrow_forwardFind the derivative of the function. 5 1 6 p(x) = -24x 5 +15xarrow_forward∞ 2n (4n)! Let R be the radius of convergence of the series -x2n. Then the value of (3" (2n)!)² n=1 sin(2R+4/R) is -0.892 0.075 0.732 -0.812 -0.519 -0.107 -0.564 0.588arrow_forward
- Find the cost function if the marginal cost function is given by C'(x) = x C(x) = 2/5 + 5 and 32 units cost $261.arrow_forwardFind the cost function if the marginal cost function is C'(x) = 3x-4 and the fixed cost is $9. C(x) = ☐arrow_forwardFor the power series ∞ (−1)" (2n+1)(x+4)” calculate Z, defined as follows: n=0 (5 - 1)√n if the interval of convergence is (a, b), then Z = sin a + sin b if the interval of convergence is (a, b), then Z = cos asin b if the interval of convergence is (a, b], then Z = sin a + cos b if the interval of convergence is [a, b], then Z = cos a + cos b Then the value of Z is -0.502 0.117 -0.144 -0.405 0.604 0.721 -0.950 -0.588arrow_forward
- H-/ test the Series 1.12 7√2 by ratio best 2n 2-12- nz by vitio test enarrow_forwardHale / test the Series 1.12 7√2 2n by ratio best 2-12- nz by vico tio test en - プ n2 rook 31() by mood fest 4- E (^)" by root test Inn 5-E 3' b. E n n³ 2n by ratio test ٤ by Comera beon Test (n+2)!arrow_forwardEvaluate the double integral ' √ √ (−2xy² + 3ry) dA R where R = {(x,y)| 1 ≤ x ≤ 3, 2 ≤ y ≤ 4} Double Integral Plot of integrand and Region R N 120 100 80- 60- 40 20 -20 -40 2 T 3 4 5123456 This plot is an example of the function over region R. The region and function identified in your problem will be slightly different. Answer = Round your answer to four decimal places.arrow_forward
- Find Te²+ dydz 0 Write your answer in exact form.arrow_forwardxy² Find -dA, R = [0,3] × [−4,4] x²+1 Round your answer to four decimal places.arrow_forwardFind the values of p for which the series is convergent. P-?- ✓ 00 Σ nº (1 + n10)p n = 1 Need Help? Read It Watch It SUBMIT ANSWER [-/4 Points] DETAILS MY NOTES SESSCALCET2 8.3.513.XP. Consider the following series. 00 Σ n = 1 1 6 n° (a) Use the sum of the first 10 terms to estimate the sum of the given series. (Round the answer to six decimal places.) $10 = (b) Improve this estimate using the following inequalities with n = 10. (Round your answers to six decimal places.) Sn + + Los f(x) dx ≤s ≤ S₁ + Jn + 1 + Lo f(x) dx ≤s ≤ (c) Using the Remainder Estimate for the Integral Test, find a value of n that will ensure that the error in the approximation s≈s is less than 0.0000001. On > 11 n> -18 On > 18 On > 0 On > 6 Need Help? Read It Watch Itarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Limits and Continuity; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=9brk313DjV8;License: Standard YouTube License, CC-BY