MATH IN OUR WORLD (VALUE EDITION)
4th Edition
ISBN: 9781266216855
Author: sobecki
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 2.3, Problem 50E
For Exercises 39–50, use the following Venn diagram to find the cardinality of each set.
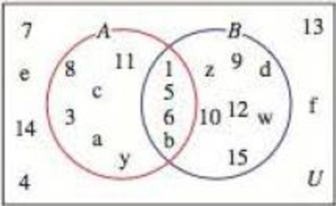
50. n(B′ ∪ (B − A))
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The function f(x) is represented by the equation, f(x) = x³ + 8x² + x − 42.
Part A: Does f(x) have zeros located at -7, 2, -3? Explain without using technology and show all work.
Part B: Describe the end behavior of f(x) without using technology.
How does the graph of f(x) = (x − 9)4 – 3 compare to the parent function g(x) = x²?
Find the x-intercepts and the y-intercept of the graph of f(x) = (x − 5)(x − 2)(x − 1) without using technology. Show all work.
Chapter 2 Solutions
MATH IN OUR WORLD (VALUE EDITION)
Ch. 2.1 - Write the set of months that end with the letter...Ch. 2.1 - Write each set, using the roster method. (a) The...Ch. 2.1 - Decide whether each statement is true or false....Ch. 2.1 - Prob. 4TTOCh. 2.1 - Use set-builder notation to designate each set,...Ch. 2.1 - Prob. 6TTOCh. 2.1 - Using the roster method, write the set of odd...Ch. 2.1 - Prob. 8TTOCh. 2.1 - Find the cardinal number of each set. (a) A = {z,...Ch. 2.1 - Prob. 10TTO
Ch. 2.1 - Prob. 11TTOCh. 2.1 - Show that the sets {North, South, East, West} and...Ch. 2.1 - Prob. 1ECh. 2.1 - Prob. 2ECh. 2.1 - Prob. 3ECh. 2.1 - List and describe three ways to write sets.Ch. 2.1 - Prob. 5ECh. 2.1 - Prob. 6ECh. 2.1 - Prob. 7ECh. 2.1 - Define the empty set and give two examples of an...Ch. 2.1 - Prob. 9ECh. 2.1 - For Exercises 922. write each set using the roster...Ch. 2.1 - For Exercises 922. write each set using the roster...Ch. 2.1 - For Exercises 922, write each set using the roster...Ch. 2.1 - For Exercises 922. write each set using the roster...Ch. 2.1 - Prob. 14ECh. 2.1 - Prob. 15ECh. 2.1 - For Exercises 922. write each set using the roster...Ch. 2.1 - Prob. 17ECh. 2.1 - For Exercises 922. write each set using the roster...Ch. 2.1 - Prob. 19ECh. 2.1 - Prob. 20ECh. 2.1 - Prob. 21ECh. 2.1 - Prob. 22ECh. 2.1 - For Exercises 2328, decide if the statement is...Ch. 2.1 - Prob. 24ECh. 2.1 - For Exercises 2328, decide if the statement is...Ch. 2.1 - Prob. 26ECh. 2.1 - Prob. 27ECh. 2.1 - Prob. 28ECh. 2.1 - For Exercises 2936, write each set, using the...Ch. 2.1 - For Exercises 2936, write each set, using the...Ch. 2.1 - For Exercises 2936, write each set, using the...Ch. 2.1 - For Exercises 2936, write each set, using the...Ch. 2.1 - Prob. 33ECh. 2.1 - Prob. 34ECh. 2.1 - Prob. 35ECh. 2.1 - Prob. 36ECh. 2.1 - Prob. 37ECh. 2.1 - Prob. 38ECh. 2.1 - Prob. 39ECh. 2.1 - Prob. 40ECh. 2.1 - Prob. 41ECh. 2.1 - Prob. 42ECh. 2.1 - For Exercises 4348, list the elements in each set....Ch. 2.1 - For Exercises 4348, list the elements in each set....Ch. 2.1 - For Exercises 4348, list the elements in each set....Ch. 2.1 - For Exercises 4348, list the elements in each set....Ch. 2.1 - Prob. 47ECh. 2.1 - Prob. 48ECh. 2.1 - Prob. 49ECh. 2.1 - For Exercises 4954, state whether each collection...Ch. 2.1 - Prob. 51ECh. 2.1 - Prob. 52ECh. 2.1 - Prob. 53ECh. 2.1 - Prob. 54ECh. 2.1 - Prob. 55ECh. 2.1 - Prob. 56ECh. 2.1 - Prob. 57ECh. 2.1 - Prob. 58ECh. 2.1 - Prob. 59ECh. 2.1 - Prob. 60ECh. 2.1 - Prob. 61ECh. 2.1 - Prob. 62ECh. 2.1 - For Exercises 6168, state whether each set is...Ch. 2.1 - For Exercises 6168, state whether each set is...Ch. 2.1 - Prob. 65ECh. 2.1 - Prob. 66ECh. 2.1 - Prob. 67ECh. 2.1 - For Exercises 6168, state whether each set is...Ch. 2.1 - For Exercises 6974, state whether each pair of...Ch. 2.1 - For Exercises 6974, state whether each pair of...Ch. 2.1 - Prob. 71ECh. 2.1 - For Exercises 6974, state whether each pair of...Ch. 2.1 - Prob. 73ECh. 2.1 - For Exercises 6974, state whether each pair of...Ch. 2.1 - For Exercises 7578, show that each pair of sets is...Ch. 2.1 - Prob. 76ECh. 2.1 - Prob. 77ECh. 2.1 - Prob. 78ECh. 2.1 - For Exercises 7986, find the cardinal number for...Ch. 2.1 - Prob. 80ECh. 2.1 - Prob. 81ECh. 2.1 - Prob. 82ECh. 2.1 - Prob. 83ECh. 2.1 - For Exercises 7986, find the cardinal number for...Ch. 2.1 - For Exercises 7986, find the cardinal number for...Ch. 2.1 - Prob. 86ECh. 2.1 - For Exercises 8792, determine whether each...Ch. 2.1 - For Exercises 8792, determine whether each...Ch. 2.1 - Prob. 89ECh. 2.1 - Prob. 90ECh. 2.1 - Prob. 91ECh. 2.1 - Prob. 92ECh. 2.1 - Prob. 93ECh. 2.1 - Prob. 94ECh. 2.1 - Excessive alcohol consumption by those aged 1824...Ch. 2.1 - Prob. 96ECh. 2.1 - Prob. 97ECh. 2.1 - 98. The rise of digital distribution for music has...Ch. 2.1 - Prob. 99ECh. 2.1 - Prob. 100ECh. 2.1 - Is {0} equivalent to ? Explain your answer.Ch. 2.1 - Write two sets that are equivalent but not equal....Ch. 2.1 - Prob. 103ECh. 2.1 - (a) List all of the different sets you can form...Ch. 2.1 - Prob. 105ECh. 2.1 - Prob. 106ECh. 2.2 - Try This One 1
Let U = {10, 20, 30, 40, 50, 60,...Ch. 2.2 - Find all subsets of B = {Verizon, T-Mobile, ATT}.Ch. 2.2 - Prob. 3TTOCh. 2.2 - Decide if each statement is true or false. (a) {8}...Ch. 2.2 - Prob. 5TTOCh. 2.2 - If A = {Cleveland, Indianapolis, Chicago, Des...Ch. 2.2 - Prob. 7TTOCh. 2.2 - Prob. 8TTOCh. 2.2 - Prob. 9TTOCh. 2.2 - Prob. 10TTOCh. 2.2 - What is a subset?Ch. 2.2 - Explain the difference between a subset and a...Ch. 2.2 - Prob. 3ECh. 2.2 - Prob. 4ECh. 2.2 - Prob. 5ECh. 2.2 - Prob. 6ECh. 2.2 - Prob. 7ECh. 2.2 - Prob. 8ECh. 2.2 - Write an example from real life that represents...Ch. 2.2 - Write an example from real life that represents...Ch. 2.2 - For Exercises 1114, let U = {2, 3, 5, 7, 11, 13,...Ch. 2.2 - For Exercises 1114, let U = {2, 3, 5, 7, 11, 13,...Ch. 2.2 - Prob. 13ECh. 2.2 - Prob. 14ECh. 2.2 - If U = the set of natural numbers and A = {4, 6,...Ch. 2.2 - Prob. 16ECh. 2.2 - Prob. 17ECh. 2.2 - Prob. 18ECh. 2.2 - Prob. 19ECh. 2.2 - Prob. 20ECh. 2.2 - Prob. 21ECh. 2.2 - Prob. 22ECh. 2.2 - Prob. 23ECh. 2.2 - Prob. 24ECh. 2.2 - For Exercises 2534, state whether each is true or...Ch. 2.2 - Prob. 26ECh. 2.2 - For Exercises 2534, state whether each is true or...Ch. 2.2 - Prob. 28ECh. 2.2 - Prob. 29ECh. 2.2 - For Exercises 2534, state whether each is true or...Ch. 2.2 - Prob. 31ECh. 2.2 - Prob. 32ECh. 2.2 - Prob. 33ECh. 2.2 - For Exercises 2534, state whether each is true or...Ch. 2.2 - Prob. 35ECh. 2.2 - Prob. 36ECh. 2.2 - Prob. 37ECh. 2.2 - Prob. 38ECh. 2.2 - Prob. 39ECh. 2.2 - Prob. 40ECh. 2.2 - Prob. 41ECh. 2.2 - Prob. 42ECh. 2.2 - Prob. 43ECh. 2.2 - Prob. 44ECh. 2.2 - Prob. 45ECh. 2.2 - Prob. 46ECh. 2.2 - Prob. 47ECh. 2.2 - Prob. 48ECh. 2.2 - Prob. 49ECh. 2.2 - Prob. 50ECh. 2.2 - Prob. 51ECh. 2.2 - Prob. 52ECh. 2.2 - Prob. 53ECh. 2.2 - For Exercises 5160, let U = {11, 12, 13, 14, 15,...Ch. 2.2 - Prob. 55ECh. 2.2 - Prob. 56ECh. 2.2 - Prob. 57ECh. 2.2 - Prob. 58ECh. 2.2 - Prob. 59ECh. 2.2 - For Exercises 5160, let U = {11, 12, 13, 14, 15,...Ch. 2.2 - Prob. 61ECh. 2.2 - Prob. 62ECh. 2.2 - Prob. 63ECh. 2.2 - For Exercises 6170, let U = {x | x N and x 25} W...Ch. 2.2 - Prob. 65ECh. 2.2 - Prob. 66ECh. 2.2 - Prob. 67ECh. 2.2 - Prob. 68ECh. 2.2 - For Exercises 6170, let U = {x | x N and x 25} W...Ch. 2.2 - Prob. 70ECh. 2.2 - Prob. 71ECh. 2.2 - Prob. 72ECh. 2.2 - Prob. 73ECh. 2.2 - Prob. 74ECh. 2.2 - Prob. 75ECh. 2.2 - Prob. 76ECh. 2.2 - Prob. 77ECh. 2.2 - Prob. 78ECh. 2.2 - Prob. 79ECh. 2.2 - Prob. 80ECh. 2.2 - Prob. 81ECh. 2.2 - Prob. 82ECh. 2.2 - For Exercises 8184, let D = {11, 12, 13, 14, 15,}...Ch. 2.2 - For Exercises 8184, let D = {11, 12, 13, 14, 15,}...Ch. 2.2 - Prob. 85ECh. 2.2 - Prob. 86ECh. 2.2 - Prob. 87ECh. 2.2 - Prob. 88ECh. 2.2 - Prob. 89ECh. 2.2 - Prob. 90ECh. 2.2 - Prob. 91ECh. 2.2 - Prob. 92ECh. 2.2 - Prob. 93ECh. 2.2 - To integrate aerobics into her exercise program,...Ch. 2.2 - Prob. 95ECh. 2.2 - Prob. 96ECh. 2.2 - Prob. 97ECh. 2.2 - Prob. 98ECh. 2.2 - Prob. 99ECh. 2.2 - Prob. 100ECh. 2.2 - Prob. 101ECh. 2.2 - Prob. 102ECh. 2.2 - Prob. 103ECh. 2.2 - Prob. 104ECh. 2.2 - Prob. 105ECh. 2.2 - Prob. 106ECh. 2.2 - Prob. 107ECh. 2.2 - Prob. 108ECh. 2.2 - Prob. 109ECh. 2.2 - Prob. 110ECh. 2.2 - Prob. 111ECh. 2.3 - Prob. 1TTOCh. 2.3 - Prob. 2TTOCh. 2.3 - Prob. 3TTOCh. 2.3 - Prob. 4TTOCh. 2.3 - Prob. 5TTOCh. 2.3 - Prob. 6TTOCh. 2.3 - Use Venn diagrams to show that (A B) = A B.Ch. 2.3 - Prob. 8TTOCh. 2.3 - Prob. 9TTOCh. 2.3 - Prob. 10TTOCh. 2.3 - Prob. 2ECh. 2.3 - Prob. 3ECh. 2.3 - Prob. 4ECh. 2.3 - Describe in your own words what De Morgans laws...Ch. 2.3 - Prob. 6ECh. 2.3 - For Exercises 730, draw a Venn diagram and shade...Ch. 2.3 - For Exercises 730, draw a Venn diagram and shade...Ch. 2.3 - Prob. 9ECh. 2.3 - Prob. 10ECh. 2.3 - Prob. 11ECh. 2.3 - Prob. 12ECh. 2.3 - For Exercises 730, draw a Venn diagram and shade...Ch. 2.3 - Prob. 14ECh. 2.3 - For Exercises 730, draw a Venn diagram and shade...Ch. 2.3 - Prob. 16ECh. 2.3 - For Exercises 730, draw a Venn diagram and shade...Ch. 2.3 - For Exercises 730, draw a Venn diagram and shade...Ch. 2.3 - For Exercises 730, draw a Venn diagram and shade...Ch. 2.3 - For Exercises 730, draw a Venn diagram and shade...Ch. 2.3 - Prob. 21ECh. 2.3 - For Exercises 730, draw a Venn diagram and shade...Ch. 2.3 - For Exercises 730, draw a Venn diagram and shade...Ch. 2.3 - Prob. 24ECh. 2.3 - For Exercises 730, draw a Venn diagram and shade...Ch. 2.3 - For Exercises 730, draw a Venn diagram and shade...Ch. 2.3 - For Exercises 730, draw a Venn diagram and shade...Ch. 2.3 - For Exercises 730, draw a Venn diagram and shade...Ch. 2.3 - For Exercises 730, draw a Venn diagram and shade...Ch. 2.3 - For Exercises 730, draw a Venn diagram and shade...Ch. 2.3 - Prob. 31ECh. 2.3 - Prob. 32ECh. 2.3 - Prob. 33ECh. 2.3 - Prob. 34ECh. 2.3 - Prob. 35ECh. 2.3 - Prob. 36ECh. 2.3 - Prob. 37ECh. 2.3 - Prob. 38ECh. 2.3 - For Exercises 3950, use the following Venn diagram...Ch. 2.3 - For Exercises 3950, use the following Venn diagram...Ch. 2.3 - Prob. 41ECh. 2.3 - For Exercises 3950, use the following Venn diagram...Ch. 2.3 - For Exercises 3950, use the following Venn diagram...Ch. 2.3 - For Exercises 3950, use the following Venn diagram...Ch. 2.3 - Prob. 45ECh. 2.3 - For Exercises 3950, use the following Venn diagram...Ch. 2.3 - For Exercises 3950, use the following Venn diagram...Ch. 2.3 - For Exercises 3950, use the following Venn diagram...Ch. 2.3 - For Exercises 3950, use the following Venn diagram...Ch. 2.3 - For Exercises 3950, use the following Venn diagram...Ch. 2.3 - For Exercises 5160, use the following information:...Ch. 2.3 - For Exercises 5160, use the following information:...Ch. 2.3 - For Exercises 5160, use the following information:...Ch. 2.3 - For Exercises 5160, use the following information:...Ch. 2.3 - For Exercises 5160, use the following information:...Ch. 2.3 - For Exercises 5160, use the following information:...Ch. 2.3 - Prob. 57ECh. 2.3 - Prob. 58ECh. 2.3 - For Exercises 5160, use the following information:...Ch. 2.3 - For Exercises 5160, use the following information:...Ch. 2.3 - Prob. 61ECh. 2.3 - Prob. 62ECh. 2.3 - Prob. 63ECh. 2.3 - Prob. 64ECh. 2.3 - Prob. 65ECh. 2.3 - Prob. 66ECh. 2.3 - Prob. 67ECh. 2.3 - Prob. 68ECh. 2.3 - Prob. 69ECh. 2.3 - Prob. 70ECh. 2.3 - Prob. 71ECh. 2.3 - Prob. 72ECh. 2.3 - Prob. 73ECh. 2.3 - In Exercises 7376, G = {people who regularly use...Ch. 2.3 - Prob. 75ECh. 2.3 - Prob. 76ECh. 2.3 - Prob. 77ECh. 2.3 - Prob. 78ECh. 2.3 - Prob. 79ECh. 2.3 - Prob. 80ECh. 2.3 - Prob. 81ECh. 2.3 - Prob. 82ECh. 2.3 - Prob. 83ECh. 2.3 - Prob. 84ECh. 2.3 - Prob. 85ECh. 2.3 - Prob. 86ECh. 2.3 - Prob. 87ECh. 2.3 - In Exercises 8792. (a) use a Venn diagram to show...Ch. 2.3 - Prob. 89ECh. 2.3 - In Exercises 8792. (a) use a Venn diagram to show...Ch. 2.3 - In Exercises 8792. (a) use a Venn diagram to show...Ch. 2.3 - In Exercises 8792. (a) use a Venn diagram to show...Ch. 2.4 - In an average year, Columbus, Ohio, has 163 days...Ch. 2.4 - According to an online survey on...Ch. 2.4 - An online music service surveyed 500 customers and...Ch. 2.4 - Three other risk factors are obesity, family...Ch. 2.4 - Prob. 1ECh. 2.4 - In a class of 25 students, 18 were math majors, 12...Ch. 2.4 - A court record search of 250 incoming freshmen at...Ch. 2.4 - Twenty-five mice were involved in a biology...Ch. 2.4 - Out of 20 students taking a midterm psychology...Ch. 2.4 - In a study of 400 entres served at 75 campus...Ch. 2.4 - The financial aid department at a college surveyed...Ch. 2.4 - The manager of a campus gym is planning the...Ch. 2.4 - One semester in a chemistry class, 14 students...Ch. 2.4 - According to a survey conducted by the National...Ch. 2.4 - Two hundred patients suffering from depression...Ch. 2.4 - A survey of 96 students on campus showed that 29...Ch. 2.4 - Of the 50 largest cities in the United States, 11...Ch. 2.4 - One hundred new books are released nationally over...Ch. 2.4 - A marketing firm is hired to conduct research into...Ch. 2.4 - The arts communities in 230 cities across the...Ch. 2.4 - A researcher was hired to examine the drinking...Ch. 2.4 - The marketing research firm of OUWant12 designed...Ch. 2.4 - Prob. 19ECh. 2.4 - Prob. 20ECh. 2.5 - Show that the set {1, 2, 3, 4, 5, } is an infinite...Ch. 2.5 - Prob. 2TTOCh. 2.5 - Prob. 3TTOCh. 2.5 - Prob. 1ECh. 2.5 - Prob. 2ECh. 2.5 - Prob. 3ECh. 2.5 - Prob. 4ECh. 2.5 - Prob. 5ECh. 2.5 - Prob. 6ECh. 2.5 - Prob. 7ECh. 2.5 - Prob. 8ECh. 2.5 - Prob. 9ECh. 2.5 - For Exercises 520, find a general term for the...Ch. 2.5 - Prob. 11ECh. 2.5 - Prob. 12ECh. 2.5 - Prob. 13ECh. 2.5 - Prob. 14ECh. 2.5 - For Exercises 520, find a general term for the...Ch. 2.5 - Prob. 16ECh. 2.5 - Prob. 17ECh. 2.5 - Prob. 18ECh. 2.5 - Prob. 19ECh. 2.5 - Prob. 20ECh. 2.5 - Prob. 21ECh. 2.5 - Prob. 22ECh. 2.5 - Prob. 23ECh. 2.5 - Prob. 24ECh. 2.5 - Prob. 25ECh. 2.5 - Prob. 26ECh. 2.5 - Prob. 27ECh. 2.5 - Prob. 28ECh. 2.5 - Prob. 29ECh. 2.5 - Prob. 30ECh. 2.5 - Prob. 31ECh. 2.5 - Prob. 32ECh. 2.5 - For Exercises 3134, show that the given set is...Ch. 2.5 - Prob. 34ECh. 2.5 - Prob. 35ECh. 2.5 - Prob. 36ECh. 2.5 - Prob. 37ECh. 2.5 - Prob. 38ECh. 2.5 - Prob. 39ECh. 2.5 - (a) Define a one-to-one correspondence between the...Ch. 2.5 - Prob. 41ECh. 2.5 - Prob. 42ECh. 2.5 - In Exercises 4146, find the cardinality of the...Ch. 2.5 - In Exercises 4146, find the cardinality of the...Ch. 2.5 - Prob. 45ECh. 2.5 - In Exercises 4146, find the cardinality of the...Ch. 2 - Prob. 1RECh. 2 - Prob. 2RECh. 2 - Prob. 3RECh. 2 - Prob. 4RECh. 2 - Prob. 5RECh. 2 - Prob. 6RECh. 2 - Prob. 7RECh. 2 - Prob. 8RECh. 2 - Prob. 9RECh. 2 - Prob. 10RECh. 2 - For Exercises 912, write each set using...Ch. 2 - Prob. 12RECh. 2 - For Exercises 1320, state whether the set is...Ch. 2 - Prob. 14RECh. 2 - Prob. 15RECh. 2 - Prob. 16RECh. 2 - Prob. 17RECh. 2 - Prob. 18RECh. 2 - Prob. 19RECh. 2 - Prob. 20RECh. 2 - For Exercises 2124, decide if the statement is...Ch. 2 - Prob. 22RECh. 2 - For Exercises 2124, decide if the statement is...Ch. 2 - For Exercises 2124, decide if the statement is...Ch. 2 - For Exercises 2124, decide if the statement is...Ch. 2 - Prob. 26RECh. 2 - Prob. 27RECh. 2 - Prob. 28RECh. 2 - Prob. 29RECh. 2 - Prob. 30RECh. 2 - Prob. 31RECh. 2 - Prob. 32RECh. 2 - Prob. 33RECh. 2 - Prob. 34RECh. 2 - Prob. 35RECh. 2 - Prob. 36RECh. 2 - Prob. 37RECh. 2 - Prob. 38RECh. 2 - Prob. 39RECh. 2 - Prob. 40RECh. 2 - Prob. 41RECh. 2 - Prob. 42RECh. 2 - Prob. 43RECh. 2 - Prob. 44RECh. 2 - Prob. 45RECh. 2 - Prob. 46RECh. 2 - Prob. 47RECh. 2 - For Exercises 4750, draw a Venn diagram and shade...Ch. 2 - Prob. 49RECh. 2 - Prob. 50RECh. 2 - If n(A) = 15, n(B) = 9, and n(A B) = 4, find n(A ...Ch. 2 - Prob. 52RECh. 2 - Prob. 53RECh. 2 - Prob. 54RECh. 2 - Prob. 55RECh. 2 - Prob. 56RECh. 2 - Prob. 57RECh. 2 - A hearing specialist conducts a study on hearing...Ch. 2 - 59. Fifty-three callers to a campus radio station...Ch. 2 - Prob. 60RECh. 2 - Prob. 61RECh. 2 - Prob. 62RECh. 2 - Prob. 63RECh. 2 - Prob. 1CTCh. 2 - Prob. 2CTCh. 2 - Prob. 3CTCh. 2 - Prob. 4CTCh. 2 - Prob. 5CTCh. 2 - Prob. 6CTCh. 2 - Prob. 7CTCh. 2 - Prob. 8CTCh. 2 - Prob. 9CTCh. 2 - Prob. 11CTCh. 2 - Prob. 12CTCh. 2 - Prob. 13CTCh. 2 - Prob. 14CTCh. 2 - Prob. 15CTCh. 2 - Prob. 16CTCh. 2 - Prob. 17CTCh. 2 - Prob. 18CTCh. 2 - Prob. 19CTCh. 2 - Prob. 20CTCh. 2 - Prob. 21CTCh. 2 - A student studying for a masters degree in sports...Ch. 2 - Prob. 23CTCh. 2 - Prob. 24CTCh. 2 - Prob. 25CTCh. 2 - Prob. 26CTCh. 2 - Prob. 27CTCh. 2 - Prob. 28CTCh. 2 - Prob. 29CTCh. 2 - For Exercises 2530, state whether each is true or...
Additional Math Textbook Solutions
Find more solutions based on key concepts
1. How much money is Joe earning when he’s 30?
Pathways To Math Literacy (looseleaf)
Is there a relationship between wine consumption and deaths from heart disease? The table gives data from 19 de...
College Algebra Essentials (5th Edition)
NOTE: Write your answers using interval notation when appropriate.
CHECKING ANALYTIC SKILLS Fill in each blank ...
Graphical Approach To College Algebra
(a) Make a stem-and-leaf plot for these 24 observations on the number of customers who used a down-town CitiBan...
APPLIED STAT.IN BUS.+ECONOMICS
Teacher Salaries
The following data from several years ago represent salaries (in dollars) from a school distri...
Elementary Statistics: A Step By Step Approach
Testing Hypotheses. In Exercises 13-24, assume that a simple random sample has been selected and test the given...
Elementary Statistics Using The Ti-83/84 Plus Calculator, Books A La Carte Edition (5th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- In a volatile housing market, the overall value of a home can be modeled by V(x) = 415x² - 4600x + 200000, where V represents the value of the home and x represents each year after 2020. Part A: Find the vertex of V(x). Show all work. Part B: Interpret what the vertex means in terms of the value of the home.arrow_forwardShow all work to solve 3x² + 5x - 2 = 0.arrow_forwardTwo functions are given below: f(x) and h(x). State the axis of symmetry for each function and explain how to find it. f(x) h(x) 21 5 4+ 3 f(x) = −2(x − 4)² +2 + -5 -4-3-2-1 1 2 3 4 5 -1 -2 -3 5arrow_forward
- The functions f(x) = (x + 1)² - 2 and g(x) = (x-2)² + 1 have been rewritten using the completing-the-square method. Apply your knowledge of functions in vertex form to determine if the vertex for each function is a minimum or a maximum and explain your reasoning.arrow_forwardTotal marks 15 3. (i) Let FRN Rm be a mapping and x = RN is a given point. Which of the following statements are true? Construct counterex- amples for any that are false. (a) If F is continuous at x then F is differentiable at x. (b) If F is differentiable at x then F is continuous at x. If F is differentiable at x then F has all 1st order partial (c) derivatives at x. (d) If all 1st order partial derivatives of F exist and are con- tinuous on RN then F is differentiable at x. [5 Marks] (ii) Let mappings F= (F1, F2) R³ → R² and G=(G1, G2) R² → R² : be defined by F₁ (x1, x2, x3) = x1 + x², G1(1, 2) = 31, F2(x1, x2, x3) = x² + x3, G2(1, 2)=sin(1+ y2). By using the chain rule, calculate the Jacobian matrix of the mapping GoF R3 R², i.e., JGoF(x1, x2, x3). What is JGOF(0, 0, 0)? (iii) [7 Marks] Give reasons why the mapping Go F is differentiable at (0, 0, 0) R³ and determine the derivative matrix D(GF)(0, 0, 0). [3 Marks]arrow_forward5. (i) Let f R2 R be defined by f(x1, x2) = x² - 4x1x2 + 2x3. Find all local minima of f on R². (ii) [10 Marks] Give an example of a function f: R2 R which is not bounded above and has exactly one critical point, which is a minimum. Justify briefly Total marks 15 your answer. [5 Marks]arrow_forward
- Total marks 15 4. : Let f R2 R be defined by f(x1, x2) = 2x²- 8x1x2+4x+2. Find all local minima of f on R². [10 Marks] (ii) Give an example of a function f R2 R which is neither bounded below nor bounded above, and has no critical point. Justify briefly your answer. [5 Marks]arrow_forward4. Let F RNR be a mapping. (i) x ЄRN ? (ii) : What does it mean to say that F is differentiable at a point [1 Mark] In Theorem 5.4 in the Lecture Notes we proved that if F is differentiable at a point x E RN then F is continuous at x. Proof. Let (n) CRN be a sequence such that xn → x ЄERN as n → ∞. We want to show that F(xn) F(x), which means F is continuous at x. Denote hnxn - x, so that ||hn|| 0. Thus we find ||F(xn) − F(x)|| = ||F(x + hn) − F(x)|| * ||DF (x)hn + R(hn) || (**) ||DF(x)hn||+||R(hn)||| → 0, because the linear mapping DF(x) is continuous and for all large nЄ N, (***) ||R(hn) || ||R(hn) || ≤ → 0. ||hn|| (a) Explain in details why ||hn|| → 0. [3 Marks] (b) Explain the steps labelled (*), (**), (***). [6 Marks]arrow_forward4. In Theorem 5.4 in the Lecture Notes we proved that if F: RN → Rm is differentiable at x = RN then F is continuous at x. Proof. Let (xn) CRN be a sequence such that x → x Є RN as n → ∞. We want F(x), which means F is continuous at x. to show that F(xn) Denote hn xnx, so that ||hn||| 0. Thus we find ||F (xn) − F(x) || (*) ||F(x + hn) − F(x)|| = ||DF(x)hn + R(hn)|| (**) ||DF(x)hn|| + ||R(hn) || → 0, because the linear mapping DF(x) is continuous and for all large n = N, |||R(hn) || ≤ (***) ||R(hn)|| ||hn|| → 0. Explain the steps labelled (*), (**), (***) [6 Marks] (ii) Give an example of a function F: RR such that F is contin- Total marks 10 uous at x=0 but F is not differentiable at at x = 0. [4 Marks]arrow_forward
- 3. Let f R2 R be a function. (i) Explain in your own words the relationship between the existence of all partial derivatives of f and differentiability of f at a point x = R². (ii) Consider R2 → R defined by : [5 Marks] f(x1, x2) = |2x1x2|1/2 Show that af af -(0,0) = 0 and -(0, 0) = 0, Jx1 მx2 but f is not differentiable at (0,0). [10 Marks]arrow_forward13) Consider the checkerboard arrangement shown below. Assume that the red checker can move diagonally upward, one square at a time, on the white squares. It may not enter a square if occupied by another checker, but may jump over it. How many routes are there for the red checker to the top of the board?arrow_forwardFill in the blanks to describe squares. The square of a number is that number Question Blank 1 of 4 . The square of negative 12 is written as Question Blank 2 of 4 , but the opposite of the square of 12 is written as Question Blank 3 of 4 . 2 • 2 = 4. Another number that can be multiplied by itself to equal 4 is Question Blank 4 of 4 .arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
What is a Linear Equation in One Variable?; Author: Don't Memorise;https://www.youtube.com/watch?v=lDOYdBgtnjY;License: Standard YouTube License, CC-BY
Linear Equation | Solving Linear Equations | What is Linear Equation in one variable ?; Author: Najam Academy;https://www.youtube.com/watch?v=tHm3X_Ta_iE;License: Standard YouTube License, CC-BY