Chapter 22, Problem 86P

a.

To determine

To Show:The net electric flux of the electric field out of the Gaussian surface is given by ${\varphi }_{net}\approx \frac{\delta E_x}{\delta x}\Delta V$

The net electric flux of the electric field out of the Gaussian surface is given by ${\varphi }_{net}\approx \frac{\delta E_x}{\delta x}\Delta V$

Given:

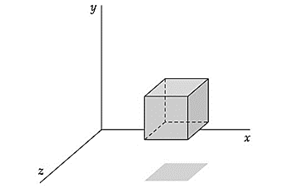
A small gaussian surface as shown

  

Formula Used:

The net flux is given by

  ${\varphi }_{net}=\varphi (x+\Delta x)-\varphi (x)$

Calculations:

The net flux is given by

  ${\varphi }_{net}=\varphi (x+\Delta x)-\varphi (x)$

Using Taylor series expansion

  ${\varphi }_{net}=\varphi (x)+(\Delta x)\varphi \text{'}(x)+1/2\varphi \text{'}\text{'}(x)+\mathrm{...}-\varphi (x)=(\Delta x)\varphi \text{'}(x)+1/2{(\Delta x)}^2\varphi \text{'}\text{'}(x)+\mathrm{..}$

Neglecting the higher than first order

  ${\varphi }_{net}\approx$

  $(\Delta x)\varphi \text{'}(x)$ (1)

As the electric field is in the x direction

  $\varphi (x)=E_x\Delta y\Delta z$

  $\varphi \text{'}(x)=\frac{\delta E_x}{\delta x}\Delta y\Delta z$

Substituting in equation 1

  ${\varphi }_{net}\approx \Delta x\frac{\delta E_x}{\delta x}\Delta y\Delta z=\frac{\delta E_x}{\delta x}\Delta x\Delta y\Delta z$

  ${\varphi }_{net}\approx \frac{\delta E_x}{\delta x}\Delta V$

Conclusion:

The net electric flux of the electric field out of the Gaussian surface is given by ${\varphi }_{net}\approx \frac{\delta E_x}{\delta x}\Delta V$

b.

Show that $\frac{\delta E_x}{\delta x}=\frac{\rho }{{\epsilon }_o}$ , where $\rho$ is the volume charge density inside the cube.

  $\frac{\delta E_x}{\delta x}=\frac{\rho }{{\epsilon }_o}$

Given:

A small gaussian surface as shown

  

  $\rho$ is the volume charge density inside the cube.

Formula Used:

Gauss’s law:

  ${\varphi }_{net}=\frac{q}{{\epsilon }_o}$

Where, q is the charge enclosed

  ${\epsilon }_o$ is the permittivity of free space.

Calculations:

  ${\varphi }_{net}=\frac{q}{{\epsilon }_o}$

  ${\varphi }_{net}=\frac{q}{{\epsilon }_o}=\frac{\rho }{{\epsilon }_o}\Delta V$

From part (a)

  ${\varphi }_{net}\approx \frac{\delta E_x}{\delta x}\Delta V$

Equating the two equations

  $\frac{\delta E_x}{\delta x}\Delta V=\frac{\rho }{{\epsilon }_o}\Delta V$

  $\frac{\delta E_x}{\delta x}=\frac{\rho }{{\epsilon }_o}$

Conclusion:

  $\frac{\delta E_x}{\delta x}=\frac{\rho }{{\epsilon }_o}$

b.

To determine

Show that $\frac{\delta E_x}{\delta x}=\frac{\rho }{{\epsilon }_o}$ , where $\rho$ is the volume charge density inside the cube.

  $\frac{\delta E_x}{\delta x}=\frac{\rho }{{\epsilon }_o}$

Given:

A small gaussian surface as shown

  

  $\rho$ is the volume charge density inside the cube.

Formula Used:

Gauss’s law:

  ${\varphi }_{net}=\frac{q}{{\epsilon }_o}$

Where, q is the charge enclosed

  ${\epsilon }_o$ is the permittivity of free space.

Calculations:

  ${\varphi }_{net}=\frac{q}{{\epsilon }_o}$

  ${\varphi }_{net}=\frac{q}{{\epsilon }_o}=\frac{\rho }{{\epsilon }_o}\Delta V$

From part (a)

  ${\varphi }_{net}\approx \frac{\delta E_x}{\delta x}\Delta V$

Equating the two equations

  $\frac{\delta E_x}{\delta x}\Delta V=\frac{\rho }{{\epsilon }_o}\Delta V$

  $\frac{\delta E_x}{\delta x}=\frac{\rho }{{\epsilon }_o}$

Conclusion:

  $\frac{\delta E_x}{\delta x}=\frac{\rho }{{\epsilon }_o}$