University Physics with Modern Physics (14th Edition)
14th Edition
ISBN: 9780321973610
Author: Hugh D. Young, Roger A. Freedman
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 22, Problem 22.35P
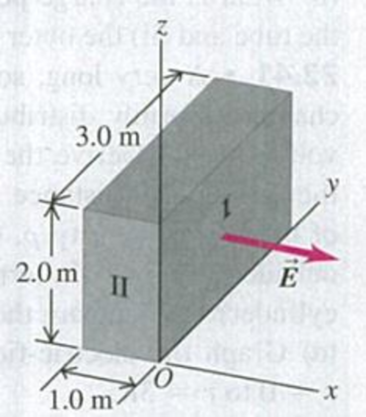
The electric field E in Fig. P22.35 is everywhere parallel to the x-axis, so the components Ey and Ez are zero. The x-component of the field Ex depends on x but not on y or z. At points in the yz-plane (where x = 0), Ex = 125 N/C. (a) What is the electric flux through surface I in Fig. P22.35? (b) What is the electric flux through surface II? (c) The volume shown is a small section of a very large insulating slab 1.0 m thick. If there is a total charge of −24.0 nC within the volume shown, what are the magnitude and direction of
Figure P22.35
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A uniform electric field of magnitude E = 435 N/C makes an angle of O = 65.0° with a plane surface of area A = 3.50 m2 as in Figure P15.40. Find the electric flux through this surface.
An infinitely long, solid cylindrical insulator has radius R1 = 14 cm and volume charge density p. The electric field at the curved surface of the cylinder is measured to have magnitude E1 = 9.4 x 103 N/C. A solid sphere with radius R1 = 30 cm has the same charge density p. Determine the electric field E2 at the sphere's surface in terms of E1, R1, and R2.
A circular loop of wire with a diameter of 0.626 m is rotated in a uniform electric field to a position where the electric flux through the
loop is a maximum. At this position, the electric flux is 7.50 x 105 N-m²/C. Determine the magnitude of the electric field.
O 2.44 × 106 N/C
O 4.24 × 106 N/C
O 1.07 x 106 N/C
O 8.88 x 105 N/C
O.6.00 x 106 N/C
eTextbook and Media
Chapter 22 Solutions
University Physics with Modern Physics (14th Edition)
Ch. 22.1 - If all of the dimensions of the box in Fig. 22.2a...Ch. 22.2 - Rank the following surfaces in order from most...Ch. 22.3 - Figure 22.16 shows six point charges that all lie...Ch. 22.4 - You place a known amount of charge Q on the...Ch. 22.5 - A hollow conducting sphere has no net charge....Ch. 22 - A rubber balloon has a single point charge in its...Ch. 22 - Suppose that in Fig. 22.15 both charges were...Ch. 22 - In Fig. 22.15, suppose a third point charge were...Ch. 22 - A certain region of space bounded by an imaginary...Ch. 22 - A spherical Gaussian surface encloses a point...
Ch. 22 - You find a sealed box on your doorstep. You...Ch. 22 - A solid copper sphere has a net positive charge....Ch. 22 - A spherical Gaussian surface encloses a point...Ch. 22 - In a conductor, one or more electrons from each...Ch. 22 - You charge up the Van de Graaff generator shown in...Ch. 22 - Lightning is a flow of electrons. The lightning...Ch. 22 - A solid conductor has a cavity in its interior....Ch. 22 - Explain this statement: In a static situation, the...Ch. 22 - In a certain region of space, the electric field E...Ch. 22 - (a) In a certain region of space, the volume...Ch. 22 - A negative charge Q is placed inside the cavity of...Ch. 22 - A flat sheet of paper of area 0.250 m2 is oriented...Ch. 22 - A flat sheet is in the shape of a rectangle with...Ch. 22 - You measure an electric field of 1.25 106 N/C at...Ch. 22 - It was shown in Example 21.10 (Section 21.5) that...Ch. 22 - A hemispherical surface with radius r in a region...Ch. 22 - The cube in Fig. E22.6 has sides of length L =...Ch. 22 - BIO As discussed in Section 22.5, human nerve...Ch. 22 - The three small spheres shown in Fig. E22.8 carry...Ch. 22 - A charged paint is spread in a very thin uniform...Ch. 22 - A point charge q1 = 4.00 nC is located on the...Ch. 22 - A 6.20 C point charge is at the center of a cube...Ch. 22 - Electric Fields in an Atom. The nuclei of large...Ch. 22 - Two very long uniform lines of charge are parallel...Ch. 22 - A solid metal sphere with radius 0.450 m carries a...Ch. 22 - How many excess electrons must be added to an...Ch. 22 - Some planetary scientists have suggested that the...Ch. 22 - A very long uniform line of charge has charge per...Ch. 22 - The electric field 0.400 m from a very long...Ch. 22 - A hollow, conducting sphere with an outer radius...Ch. 22 - (a) At a distance of 0.200 cm from the center or a...Ch. 22 - The electric field at a distance of 0.145 m from...Ch. 22 - A point charge of 3.00 C is located in the center...Ch. 22 - CP An electron is released from rest at a distance...Ch. 22 - Charge Q is distributed uniformly throughout the...Ch. 22 - A conductor with an inner cavity, like that shown...Ch. 22 - A very large, horizontal, nonconducting sheet of...Ch. 22 - Apply Gausss law to the Gaussian surfaces S2, S3,...Ch. 22 - A square insulating sheet 80.0 cm on a side is...Ch. 22 - An infinitely long cylindrical conductor has...Ch. 22 - Two very large, nonconducting plastic sheets, each...Ch. 22 - CP At time t = 0 a proton is a distance of 0.360 m...Ch. 22 - CP A very small object with mass 8.20 109 kg and...Ch. 22 - CP A small sphere with mass 4.00 106 kg and...Ch. 22 - A cube has sides of length L = 0.300 m. One corner...Ch. 22 - The electric field E in Fig. P22.35 is everywhere...Ch. 22 - CALC In a region of space there is an electric...Ch. 22 - The electric field E1 at one face of a...Ch. 22 - A long line carrying a uniform linear charge...Ch. 22 - The Coaxial Cable. A long coaxial cable consists...Ch. 22 - A very long conducting tube (hollow cylinder) has...Ch. 22 - A very long, solid cylinder with radius R has...Ch. 22 - A Sphere in a Sphere. A solid conducting sphere...Ch. 22 - A solid conducting sphere with radius R that...Ch. 22 - A conducting spherical shell with inner radius a...Ch. 22 - Concentric Spherical Shells. A small conducting...Ch. 22 - Repeat Problem 22.45, but now let the outer shell...Ch. 22 - Prob. 22.47PCh. 22 - A solid conducting sphere with radius R carries a...Ch. 22 - CALC An insulating hollow sphere has inner radius...Ch. 22 - CP Thomsons Model of the Atom. Early in the 20th...Ch. 22 - Thomsons Model of the Atom, Continued. Using...Ch. 22 - (a) How many excess electrons must be distributed...Ch. 22 - CALC A nonuniform, but spherically symmetric,...Ch. 22 - A Uniformly Charged Slab. A slab of insulating...Ch. 22 - CALC A Nonuniformly Charged Slab. Repeat Problem...Ch. 22 - CALC A nonuniform, but spherically symmetric,...Ch. 22 - (a) An insulating sphere with radius a has a...Ch. 22 - A very long, solid insulating cylinder has radius...Ch. 22 - DATA In one experiment the electric field is...Ch. 22 - DATA The electric field is measured for points at...Ch. 22 - DATA The volume charge density for a spherical...Ch. 22 - CP CALC A region in space contains a total...Ch. 22 - Suppose that to repel electrons in the radiation...Ch. 22 - What is the magnitude of E just outside the...Ch. 22 - SPACE RADIATION SHIELDING. One of the hazards...Ch. 22 - SPACE RADIATION SHIELDING. One of the hazards...
Additional Science Textbook Solutions
Find more solutions based on key concepts
Express the unit vectors in terms of (that is, derive Eq. 1.64). Check your answers several ways Also work o...
Introduction to Electrodynamics
Give the metric prefix for each value.
7. 1,000,000
Applied Physics (11th Edition)
** You measure the focal length of a concave lens by first forming a real image of a light source using a conve...
College Physics
A balloon contains 0.30 mol of helium. It rises, while maintaining a constant 300-K temperature, to an altitude...
Essential University Physics: Volume 1 (3rd Edition)
3. What is free-fall, and why does it make you weightless? Briefly describe why astronauts are weightless in th...
The Cosmic Perspective (8th Edition)
How much work is required to increase the kinetic energy of a motor scooter by 4000 J.
Conceptual Integrated Science
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A solid plastic sphere of radius R1 = 8.00 cm is concentric with an aluminum spherical shell with inner radius R2 = 14.0 cm and outer radius R3 = 17.0 cm (Fig. P25.67). Electric field measurements are made at two points: At a radial distance of 34.0 cm from the center, the electric field has magnitude 1.70 103 N/C and is directed radially outward, and at a radial distance of 12.0 cm from the center, the electric field has magnitude 9.10 104 N/C and is directed radially inward. What are the net charges on a. the plastic sphere and b. the aluminum spherical shell? c. What are the charges on the inner and outer surfaces of the aluminum spherical shell? FIGURE P25.67arrow_forwardA slab of insulating material has a nonuniform positive charge density ρ = Cx2, where x is measured from the center of the slab as shown and C is a constant. The slab is infinite in the y and z directions. Derive expressions for the electric field in (a) the exterior regions (|x| > d/2) and (b) the interior region of the slab (-d/2 < x < d/2).arrow_forwardThere is a rectangle of length 2.70 cm and width 1.50 cm in the xy-plane. If the electric field can be expressed by (50.0i^i^ +160. k^k^) N/C, what is the flux through the rectangle? 0.0648 N m2/C 0 N m2/C 0.0203 N m2/C 0.0679 N m2/Carrow_forward
- Figure P15.49 shows a closed cylinder with cross-sectional area A = 2.00 m². The con- stant electric field É has mag- nitude 3.50 x 10% N/C and is directed vertically upward, perpendicular to the cylinder's top and bottom surfaces so that no field lines pass through the curved surface. Calculate the electric flux through the cylinder's (a) top and (b) bottom surfaces. (c) Determine the amount of charge inside the cylinder. Figure P15.49arrow_forwardConsider the uniform electric field E = (3.5 j + 3.5 k) × 103 N/C. a) Calculate the electric flux through a circular area of radius 1.75 m that lies in the yz-plane. Give your answer in N·m2/C. b) Repeat the electric flux calculation for the circular area for the case when its area vector is directed at 45° above the xy-plane. Give your answer in N·m2/C.arrow_forwardA uniform electric field of magnitude E = 435 N/C makes an angle of θ = 65.0° with a plane surface of area A = 3.50 m2 as in Figure P15.44. Find the electric flux through this surface.arrow_forward
- A long, thin straight wire with linear charge density A runs down the center of a thin, hollow metal cylinder of radius R. The . cylinder has a net linear charge density 2A. Assume A is positive. esc 1 BA Q A 1 option Z 2 W S X H command # 3 20 E D $ 4 C ▾ Part A Y 888 FA R F Find expressions for the magnitude of the electric field strength inside the cylinder, r R. Give your answer as a multiple of X/co. Express your answer in terms of some or all of the variables R, r, and the constant as a multiple of ratio of charge density A to vacuum permittivity Co. 195| ΑΣΦΑ 3 2πE Provide Feedback E- Submit X Incorrect; Try Again; 4 attempts remaining % 5 V 20 T Previous Answers Request Answer G 6 MacBook Air B Y H B ? & 7 U N 8 4 DI 9 M I O K DE MOSISO > } ✓ delarrow_forwardAll or nonearrow_forwardA thin, square, conducting plate 54.0 cm on a side lies in the xy plane. A total charge of 3.20 x 10-8 C is placed on the plate. You may assume the charge density is uniform. (a) Find the charge density on each face of the plate. C/m² (b) Find the electric field just above the plate. magnitude N/C direction upward ◊ (c) Find the electric field just below the plate. magnitude N/C direction downward ↑arrow_forward
- Positive charge is distributed in a sphere of radius R that is centered at the origin. Inside the sphere, the electric field is Ē(r) = kr-1/4 f, where k is a positive constant. There is no charge outside the sphere. a) How is the charge distributed inside the sphere? In particular, find an equation for the charge density, p. b) Determine the electric field, E(r), for r > R (outside the sphere). c) What is the potential difference between the center of the sphere (r = 0) and the surface of the sphere (r = R)? d) What is the energy stored in this electric charge configuration?arrow_forwardA solid insulating sphere of radius 0.06 cm carries a total charge of 30 nC. Concentric with this sphere is a conducting spherical shell with an inner radius of 0.13 cm and an outer radius of 0.17 cm and carrying a total charge of -15 nC. Find the magnitude of the electric field at r = 0.05 cm from the center of the two spheres and shell. O 1.248x105 A N O 1.248x108 N C 6.241x106 N O 6.241æ108 Narrow_forwardA uniform electric field of magnitude E = 26 N/C points along the x-axis. A circular loop of radius R = 14 cm is centered at the origin with the normal to the loop pointing 0 = 15 degrees above the x-axis. Calculate the electric flux in units of N·m²/C that passes through the loop.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Electric Fields: Crash Course Physics #26; Author: CrashCourse;https://www.youtube.com/watch?v=mdulzEfQXDE;License: Standard YouTube License, CC-BY