
a.
To determine: The futures price for contract maturity dates on February 14, 2016; May 21 2016 and November 18, 2016 assuming that the interest rate is 3% per year, stock index- 2,000, dividend yield of 2.0%.
Introduction:
Spot-futures parity relationship: It shows the relationship between the futures price andthe spot price. Sometimes, there is a difference between the futures price andthe spot price. It may be due to changes in interest rates, expiry time and dividends paid. So, this difference has to be equated. The mathematical equation which balances the underlying price and its future price may be termed as spot-future parity.
a.
Answer to Problem 17PS
The future prices as on maturity date is as follows:
| Current date January 1, 2016 | 2000.00 |
| February 14, 2016 | 2002.40 |
| May 21, 2016 | 2022.93 |
| November 18,2016 | 2051.71 |
Explanation of Solution
Current date= January 1, 2016
Interest rate per year = 3%
Stock index pay dividend of 2% at 2000
Dividend yield=2%
From the given information, let us calculate the future price.
The formula to be used here is:
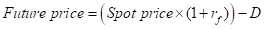
Where,
Spot price= Price of the stock in cash market;
rf= Risk -free rate of interest;
D=Dividend paid by the company.
We should be aware of the fact that T-Bill or treasury bills and Government securities carry risk-free interest rate.
Since the future price expires in a short time, the above formula needs to be modified. The modified formula is as follows:

Where,
x= number of expiry days;
Spot price= Price of the stock in cash market;
rf= Risk -free rate of interest;
D=Dividend paid by the company.
So, let us now calculate the future prices:-
i) When the maturity date is February 14,2016
The risk-free interest rate is given for the whole year. Since we are given three different periods, we have to calculate number of days in each case.
In this case, Number of days= January 1,2016 to February 14, 2016

So now, we have to calculate the risk-free interest rate for 45 days.
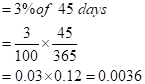
In the same way, even the dividend date of 2% is given for the entire year.
So, the dividend earned for 45 days would be
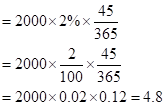
So, let us now substitute the value in the given formula:

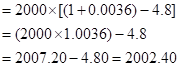
Hence the
ii) When the maturity date is May 21,2016
In this case, Number of days= January 1,2016 to May 21, 2016
=January+February+March+April+21 days of May= 141 days
So now, we have to calculate the risk-free interest rate for 141 days.
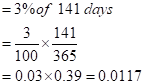
In the same way, even the dividend date of 2% is given for the entire year.
So, the dividend earned for 141 days would be
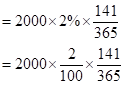
So, let us now substitute the value in the given formula:
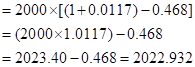
Hence the future value is 2022.932 when the maturity date is May 21, 2016.
iii) When the maturity date is November 18, 2016.
In this case, Number of days= January 1,2016 to May 21, 2016
=January+February+March+April+May+June+July+August+September+October+18 days of November= 322 days
So now, we have to calculate the risk-free interest rate for 322 days.
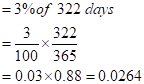
In the same way, even the dividend date of 2% is given for the entire year.
So, the dividend earned for 322 days would be
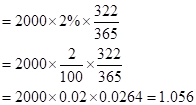
So, let us now substitute the value in the given formula:
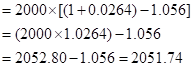
Hence the future value is 2051.74 when the maturity date is November 18, 2016.
b.
To determine: The term structure of future prices if the dividend yield is higher than the risk-free rate.
Introduction:
Dividend yield: It is supposed to be the amount of money paid by the company to its shareholders. Normally, dividend yield is calculated for one year of investment and is represented in terms of percentages.
b.
Answer to Problem 17PS
The future prices as on maturity date is as follows:
| February 14, 2016 | 1997.60 |
| May 21, 2016 | 2007.80 |
| November 18,2016 | 1982.40 |
Explanation of Solution
Current date= January 1, 2016
Interest rate per year = 3%
Stock index pay dividend of 2% at 2000
Dividend yield=2%
Let us consider the dividend yield to be 4%.
Let us now calculate the term structure of future prices if the dividend yield is 4%.
iv) When the maturity date is February 14,2016
The risk-free interest rate is given for the whole year. Since we are given three different periods, we have to calculate number of days in each case.
So now, we have to calculate the risk-free interest rate for 45 days.
From the above calculation now we are aware that number of days in this case =45 days and the risk-free interest rate for 45 days is 0.0036
The dividend date of 4% is given for the entire year.
So, the dividend earned for 45 days would be
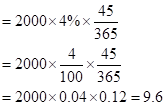
So, let us now substitute the value in the given formula:
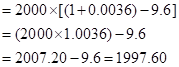
Hence the future value is 1997.60 when the maturity date is February 14, 2016.
v) When the maturity date is May 21,2016
In this case, the number of days is 141 days and the risk-free interest rate for 141 days is 0.0117.
In the same way, even the dividend date of 4% is given for the entire year.
So, the dividend earned for 141 days would be
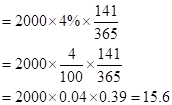
So, let us now substitute the value in the given formula:

Hence the future value is 2007.80 when the maturity date is May 21, 2016.
vi) When the maturity date is November 18, 2016.
In this case, the number of days is 322 days and the risk-free interest rate for 322 days is 0.0264.
In the same way, even the dividend date of 4% is given for the entire year.
So, the dividend earned for 322 days would be
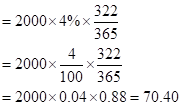
So, let us now substitute the value in the given formula:

Hence the future value is 1982.40 when the maturity date is November 18, 2016.
We can conclude that an increase in dividend yield is showing a decrease in the future prices.
Want to see more full solutions like this?
- You invest $5,000 in a project, and it generates $1,250 annually. How long will it take to recover your investment? Exparrow_forwardThe value of an investment grows from $10,000 to $15,000 in 3 years. What is the CAGR?Soovearrow_forwardSuppose that the treasurer of IBM has an extra cash reserve of $100,000,000 to invest for six months. The six-month interest rate is 9 percent per annum in the United States and 8 percent per annum in Germany. Currently, the spot exchange rate is €1.07 per dollar and the six-month forward exchange rate is €1.05 per dollar. The treasurer of IBM does not wish to bear any exchange risk. Where should they invest to maximize the return? Required: The maturity value in six months if the extra cash reserve is invested in Germany:arrow_forward
- The value of an investment grows from $10,000 to $15,000 in 3 years. What is the CAGR?arrow_forwardYou invest $5,000 in a project, and it generates $1,250 annually. How long will it take to recover your investment?arrow_forwardA company pays an annual dividend of $3 per share, and the current stock price is $50. What is the dividend yield?arrow_forward
- You invest $1,000 in a stock, and after 2 years, it grows to $1,200. What is the annual return?arrow_forwardYou invest $1,000 in a stock, and after 2 years, it grows to $1,200. What is the annual return? Exparrow_forwardWells and Associates has EBIT of $ 72800. Interest costs are $ 18400, and the firm has 15600 shares of common stock outstanding. Assume a 40 % tax rate. a. Use the degree of financial leverage (DFL) formula to calculate the DFL for the firm. b. Using a set of EBIT -EPS axes, plot Wells and Associates' financing plan. c. If the firm also has 1200 shares of preferred stock paying a $ 5.75 annual dividend per share, what is the DFL? d. Plot the financing plan, including the 1200 shares of $ 5.75 preferred stock, on the axes used in part (b). e. Briefly discuss the graph of the two financing plans.arrow_forward
- You invest $5,000 for 3 years at an annual interest rate of 6%. The interest is compounded annually. Need helparrow_forwardWhat is the future value of $500 invested for 3 years at an annual compound interest rate of 4%? Explarrow_forwardYou invest $5,000 for 3 years at an annual interest rate of 6%. The interest is compounded annually.arrow_forward
