Trigonometry plus MyLab Math with Pearson eText -- Access Card Package (11th Edition)
Trigonometry plus MyLab Math with Pearson eText -- Access Card Package (11th Edition)
11th Edition
ISBN: 9780134307008
Author: Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher: PEARSON
bartleby

Videos

Textbook Question
Book Icon
Chapter 2.1, Problem 71E

Consider an equilateral triangle with each side having length 2k.

(a) What is the measure of each angle?

(b) Label one angle A. Drop a perpendicular from A to the side opposite A. Two 30° angles are formed at A, and two right triangles are formed. What is the length of the sides opposite the 30° angles?

(c) What is the length of the perpendicular in part (b)?

(d) From the results of parts (a)-(c), complete the following statement:

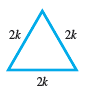
Chapter 2.1, Problem 71E, Consider an equilateral triangle with each side having length 2k. (a) What is the measure of each

In a 30°-60° right triangle, the hypotenuse is always _______ times as long as the shorter leg, and the longer leg has a length that is _______ times as long as that of the shorter leg. Also, the shorter leg is opposite the _______ angle, and the longer leg is opposite the _____ angle.

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 2.1, Problem 70E
Next
Chapter 2.1, Problem 72E
Students have asked these similar questions
Make M the subject: P=2R(M/√M-R)
Direction: This is about Maritime course, Do a total of 6 (six) of this. Strictly write this only in bond paper. COMPLETE TOPIC AND INSTRUCTION IS ALREADY PROVIDED IN THE PICTURE.   NOTE: strictly use nautical almanac. This is about maritime navigation.
Find the points of intersections of the function f(x) and its derivative. f(x)=(2x-3)√x

Chapter 2 Solutions

Trigonometry plus MyLab Math with Pearson eText -- Access Card Package (11th Edition)

Ch. 2.1 - CONCEPT PREVIEW Match each trigonometric function...Ch. 2.1 - CONCEPT PREVIEW Match each trigonometric function...Ch. 2.1 - CONCEPT PREVIEW Match each trigonometric...Ch. 2.1 - CONCEPT PREVIEW Match each trigonometric function...Ch. 2.1 - CONCEPT PREVIEW Match each trigonometric function...Ch. 2.1 - CONCEPT PREVIEW Match each trigonometric...Ch. 2.1 - Find exact values or expressions for sin A, cos A,...Ch. 2.1 - Find exact values or expressions for sin A, cos A,...Ch. 2.1 - Find exact values or expressions for sin A, cos A,...Ch. 2.1 - Find exact values or expressions for sin A, cos A,...
Ch. 2.1 - Suppose ABC is a right triangle with sides of...Ch. 2.1 - Suppose ABC is a right triangle with sides of...Ch. 2.1 - Suppose ABC is a right triangle with sides of...Ch. 2.1 - Suppose ABC is a right triangle with sides of...Ch. 2.1 - a=3,c=10 Suppose ABC is a right triangle with...Ch. 2.1 - Suppose ABC is a right triangle with sides of...Ch. 2.1 - Suppose ABC is a right triangle with sides of...Ch. 2.1 - Suppose ABC is a right triangle with sides of...Ch. 2.1 - Suppose ABC is a right triangle with sides of...Ch. 2.1 - 20. Concept Check Give the six cofunction...Ch. 2.1 - Write each function in terms of its cofunction....Ch. 2.1 - Write each function in terms of its cofunction....Ch. 2.1 - Write each function in terms of its cofunction....Ch. 2.1 - Write each function in terms of its cofunction....Ch. 2.1 - Write each function in terms of its cofunction....Ch. 2.1 - Write each function in terms of its cofunction....Ch. 2.1 - Write each function in terms of its cofunction....Ch. 2.1 - Write each function in terms of its cofunction....Ch. 2.1 - Write each function in terms of its cofunction....Ch. 2.1 - 30. Concept Check With a calculator, evaluate...Ch. 2.1 - Find one solution for each equation. Assume that...Ch. 2.1 - Find one solution for each equation. Assume that...Ch. 2.1 - Find one solution for each equation. Assume that...Ch. 2.1 - Find one solution for each equation. Assume that...Ch. 2.1 - Find one solution for each equation. Assume that...Ch. 2.1 - Find one solution for each equation. Assume that...Ch. 2.1 - Find one solution for each equation. Assume that...Ch. 2.1 - Find one solution for each equation. Assume that...Ch. 2.1 - Find one solution for each equation. Assume that...Ch. 2.1 - Find one solution for each equation. Assume that...Ch. 2.1 - Determine whether each statement is true or...Ch. 2.1 - Determine whether each statement is true or...Ch. 2.1 - Determine whether each statement is true or...Ch. 2.1 - Determine whether each statement is true or...Ch. 2.1 - Determine whether each statement is true or false....Ch. 2.1 - Determine whether each statement is true or false....Ch. 2.1 - Determine whether each statement is true or false....Ch. 2.1 - Determine whether each statement is true or...Ch. 2.1 - Give the exact value of each expression. See...Ch. 2.1 - Give the exact value of each expression. See...Ch. 2.1 - Give the exact value of each expression. See...Ch. 2.1 - Give the exact value of each expression. See...Ch. 2.1 - Give the exact value of each expression. See...Ch. 2.1 - Give the exact value of each expression. See...Ch. 2.1 - Give the exact value of each expression. See...Ch. 2.1 - Give the exact value of each expression. See...Ch. 2.1 - Give the exact value of each expression. See...Ch. 2.1 - Give the exact value of each expression. See...Ch. 2.1 - Give the exact value of each expression. See...Ch. 2.1 - Give the exact value of each expression. See...Ch. 2.1 - Give the exact value of each expression. See...Ch. 2.1 - Give the exact value of each expression. See...Ch. 2.1 - Give the exact value of each expression. See...Ch. 2.1 - Give the exact value of each expression. See...Ch. 2.1 - Prob. 65ECh. 2.1 - Prob. 66ECh. 2.1 - Prob. 67ECh. 2.1 - Prob. 68ECh. 2.1 - Prob. 69ECh. 2.1 - Prob. 70ECh. 2.1 - Consider an equilateral triangle with each side...Ch. 2.1 - Prob. 72ECh. 2.1 - Find the exact value of the variables in each...Ch. 2.1 - Find the exact value of the variables in each...Ch. 2.1 - Find the exact value of the variables in each...Ch. 2.1 - Find the exact value of the variables in each...Ch. 2.1 - Find a formula for the area of each figure in...Ch. 2.1 - Find a formula for the area of each figure in...Ch. 2.1 - Prob. 79ECh. 2.1 - Concept Check Suppose we know the length of one...Ch. 2.1 - Prob. 81ECh. 2.1 - Prob. 82ECh. 2.1 - Prob. 83ECh. 2.1 - The figure shows a 45° central angle in a circle...Ch. 2.2 - The value of sin 240 is _____ because 240 is in...Ch. 2.2 - CONCEPT PREVIEW Fill in the blanks to correctly...Ch. 2.2 - CONCEPT PREVIEW Fill in the blanks to correctly...Ch. 2.2 - CONCEPT PREVIEW Fill in the blanks to correctly...Ch. 2.2 - Prob. 5ECh. 2.2 - Concept Check Match each angle in Column I with...Ch. 2.2 - Concept Check Match each angle in Column I with...Ch. 2.2 - Concept Check Match each angle in Column I with...Ch. 2.2 - Prob. 9ECh. 2.2 - Concept Check Match each angle in Column I with...Ch. 2.2 - Complete the table with exact trigonometric...Ch. 2.2 - Complete the table with exact trigonometric...Ch. 2.2 - Prob. 13ECh. 2.2 - Prob. 14ECh. 2.2 - Complete the table with exact trigonometric...Ch. 2.2 - Complete the table with exact trigonometric...Ch. 2.2 - Prob. 17ECh. 2.2 - Prob. 18ECh. 2.2 - Find exact values of the six trigonometric...Ch. 2.2 - Find exact values of the six trigonometric...Ch. 2.2 - Find exact values of the six trigonometric...Ch. 2.2 - Find exact values of the six trigonometric...Ch. 2.2 - Find exact values of the six trigonometric...Ch. 2.2 - Prob. 24ECh. 2.2 - Find exact values of the six trigonometric...Ch. 2.2 - Find exact values of the six trigonometric...Ch. 2.2 - Find exact values of the six trigonometric...Ch. 2.2 - Find exact values of the six trigonometric...Ch. 2.2 - Find exact values of the six trigonometric...Ch. 2.2 - Find exact values of the six trigonometric...Ch. 2.2 - Find exact values of the six trigonometric...Ch. 2.2 - Find exact values of the six trigonometric...Ch. 2.2 - Find exact values of the six trigonometric...Ch. 2.2 - Find exact values of the six trigonometric...Ch. 2.2 - Find exact values of the six trigonometric...Ch. 2.2 - Prob. 36ECh. 2.2 - Find the exact value of each expression. See...Ch. 2.2 - Find the exact value of each expression. See...Ch. 2.2 - Find the exact value of each expression. See...Ch. 2.2 - Find the exact value of each expression. See...Ch. 2.2 - Find the exact value of each expression. See...Ch. 2.2 - Prob. 42ECh. 2.2 - Prob. 43ECh. 2.2 - Prob. 44ECh. 2.2 - Evaluate each expression. See Example 4. 45....Ch. 2.2 - Evaluate each expression. See Example 4. 46....Ch. 2.2 - Evaluate each expression. See Example 4. 2 tan2...Ch. 2.2 - Evaluate each expression. See Example 4. cot2 135 ...Ch. 2.2 - Evaluate each expression. See Example 4. sin2 225 ...Ch. 2.2 - Evaluate each expression. See Example 4. cot2 90 ...Ch. 2.2 - Prob. 51ECh. 2.2 - Prob. 52ECh. 2.2 - Determine whether each statement is true or false....Ch. 2.2 - Prob. 54ECh. 2.2 - Determine whether each statement is true or...Ch. 2.2 - Determine whether each statement is true or false....Ch. 2.2 - Determine whether each statement is true or false....Ch. 2.2 - Determine whether each statement is true or false....Ch. 2.2 - Prob. 59ECh. 2.2 - Prob. 60ECh. 2.2 - Find all values of θ, if θ is in the interval...Ch. 2.2 - Find all values of θ, if θ is in the interval...Ch. 2.2 - Find all values of , if is in the interval [0,...Ch. 2.2 - Prob. 64ECh. 2.2 - Find all values of θ, if θ is in the interval...Ch. 2.2 - Find all values of θ, if θ is in the interval...Ch. 2.2 - Find all values of , if is in the interval [0,...Ch. 2.2 - Find all values of θ, if θ is in the interval...Ch. 2.2 - Find all values of , if is in the interval [0,...Ch. 2.2 - Find all values of , if is in the interval [0,...Ch. 2.2 - Find all values of θ, if θ is in the interval...Ch. 2.2 - Find all values of , if is in the interval [0,...Ch. 2.2 - Concept Check Find the coordinates of the point P...Ch. 2.2 - Concept Check Find the coordinates of the point P...Ch. 2.2 - Prob. 75ECh. 2.2 - Prob. 76ECh. 2.2 - Suppose is in the interval (90, 180). Find the...Ch. 2.2 - Prob. 78ECh. 2.2 - Prob. 79ECh. 2.2 - Prob. 80ECh. 2.2 - Prob. 81ECh. 2.2 - Prob. 82ECh. 2.2 - Concept Check Work each problem. 83. Why is sin...Ch. 2.2 - Prob. 84ECh. 2.2 - Prob. 85ECh. 2.2 - Prob. 86ECh. 2.2 - Concept Check Work each problem. For what angles ...Ch. 2.2 - Concept Check Work each problem. For what angles ...Ch. 2.3 - CONCEPT PREVIEW Match each trigonometric function...Ch. 2.3 - CONCEPT PREVIEW Match each trigonometric function...Ch. 2.3 - CONCEPT PREVIEW Match each trigonometric function...Ch. 2.3 - CONCEPT PREVIEW Match each trigonometric function...Ch. 2.3 - CONCEPT PREVIEW Match each trigonometric function...Ch. 2.3 - CONCEPT PREVIEW Match each trigonometric function...Ch. 2.3 - CONCEPT PREVIEW Match each trigonometric function...Ch. 2.3 - CONCEPT PREVIEW Match each trigonometric function...Ch. 2.3 - CONCEPT PREVIEW Match each trigonometric function...Ch. 2.3 - CONCEPT PREVIEW Match each trigonometric...Ch. 2.3 - Use a calculator to approximate the value of each...Ch. 2.3 - Use a calculator to approximate the value of each...Ch. 2.3 - Use a calculator to approximate the value of each...Ch. 2.3 - Use a calculator to approximate the value of...Ch. 2.3 - Use a calculator to approximate the value of each...Ch. 2.3 - Use a calculator to approximate the value of each...Ch. 2.3 - Use a calculator to approximate the value of each...Ch. 2.3 - Use a calculator to approximate the value of each...Ch. 2.3 - Use a calculator to approximate the value of each...Ch. 2.3 - Use a calculator to approximate the value of each...Ch. 2.3 - Use a calculator to approximate the value of each...Ch. 2.3 - Use a calculator to approximate the value of each...Ch. 2.3 - Use a calculator to approximate the value of each...Ch. 2.3 - Use a calculator to approximate the value of each...Ch. 2.3 - Use a calculator to approximate the value of each...Ch. 2.3 - Use a calculator to approximate the value of each...Ch. 2.3 - Use a calculator to approximate the value of each...Ch. 2.3 - Use a calculator to approximate the value of each...Ch. 2.3 - Find a value of in the interval [0, 90) that...Ch. 2.3 - Find a value of in the interval [0, 90) that...Ch. 2.3 - Prob. 31ECh. 2.3 - Find a value of θ in the interval [0°, 90°) that...Ch. 2.3 - Find a value of θ in the interval [0°, 90°) that...Ch. 2.3 - Find a value of θ in the interval [0°, 90°) that...Ch. 2.3 - Find a value of in the interval [0, 90) that...Ch. 2.3 - Find a value of θ in the interval [0°, 90°) that...Ch. 2.3 - Find a value of θ in the interval [0°, 90°) that...Ch. 2.3 - Find a value of θ in the interval [0°, 90°) that...Ch. 2.3 - Find a value of in the interval [0, 90) that...Ch. 2.3 - Find a value of θ in the interval [0°, 90°) that...Ch. 2.3 - Prob. 41ECh. 2.3 - Prob. 42ECh. 2.3 - 43. What value of A, to the nearest degree,...Ch. 2.3 - 44. What value of A will produce the output (in...Ch. 2.3 - Use a calculator to evaluate each expression. 45....Ch. 2.3 - Use a calculator to evaluate each expression. cos...Ch. 2.3 - Prob. 47ECh. 2.3 - Prob. 48ECh. 2.3 - Prob. 49ECh. 2.3 - Prob. 50ECh. 2.3 - Use a calculator to decide whether each statement...Ch. 2.3 - Use a calculator to decide whether each statement...Ch. 2.3 - Use a calculator to decide whether each statement...Ch. 2.3 - Use a calculator to decide whether each statement...Ch. 2.3 - Use a calculator to decide whether each statement...Ch. 2.3 - Use a calculator to decide whether each statement...Ch. 2.3 - Use a calculator to decide whether each statement...Ch. 2.3 - Prob. 58ECh. 2.3 - Use a calculator to decide whether each statement...Ch. 2.3 - Prob. 60ECh. 2.3 - Use a calculator to decide whether each statement...Ch. 2.3 - Use a calculator to decide whether each statement...Ch. 2.3 - Find two angles in the interval [0, 360) that...Ch. 2.3 - Find two angles in the interval [0, 360) that...Ch. 2.3 - Find two angles in the interval [0°, 360°) that...Ch. 2.3 - Prob. 66ECh. 2.3 - Find two angles in the interval [0, 360) that...Ch. 2.3 - Find two angles in the interval [0, 360) that...Ch. 2.3 - Find the grade resistance, to the nearest ten...Ch. 2.3 - Find the grade resistance, to the nearest ten...Ch. 2.3 - A 2600-lb car traveling downhill has a grade...Ch. 2.3 - 72. A 3000-lb car traveling uphill has a grade...Ch. 2.3 - A car traveling on a 2.7 uphill grade has a grade...Ch. 2.3 - A car traveling on a 3 downhill grade has a grade...Ch. 2.3 - Prob. 75ECh. 2.3 - 76. Complete the table for values of sin θ, tan...Ch. 2.3 - Prob. 77ECh. 2.3 - Prob. 78ECh. 2.3 - Prob. 79ECh. 2.3 - Prob. 80ECh. 2.3 - (Modeling) Speed of Light When a light ray...Ch. 2.3 - Prob. 82ECh. 2.3 - Prob. 83ECh. 2.3 - Modeling) Fish's View of the World The figure...Ch. 2.3 - Prob. 85ECh. 2.3 - Prob. 86ECh. 2.3 - Prob. 87ECh. 2.3 - Prob. 88ECh. 2.3 - (Modeling) Measuring Speed by Radar Any offset...Ch. 2.3 - (Modeling) Measuring Speed by Radar Any offset...Ch. 2.3 - Prob. 91ECh. 2.3 - Prob. 92ECh. 2.3 - Find exact values of the six trigonometric...Ch. 2.3 - Prob. 2QCh. 2.3 - Prob. 3QCh. 2.3 - Prob. 4QCh. 2.3 - Prob. 5QCh. 2.3 - Prob. 6QCh. 2.3 - Prob. 7QCh. 2.3 - Prob. 8QCh. 2.3 - Prob. 9QCh. 2.3 - Prob. 10QCh. 2.3 - Prob. 11QCh. 2.3 - Find a value of θ in the interval [0°, 90°) that...Ch. 2.3 - Prob. 13QCh. 2.3 - Prob. 14QCh. 2.3 - Prob. 15QCh. 2.4 - CONCEPT PREVIEW Match each equation in Column I...Ch. 2.4 - CONCEPT PREVIEW Match each equation in Column I...Ch. 2.4 - CONCEPT PREVIEW Match each equation in Column I...Ch. 2.4 - CONCEPT PREVIEW Match each equation in Column I...Ch. 2.4 - CONCEPT PREVIEW Match each equation in Column I...Ch. 2.4 - CONCEPT PREVIEW Match each equation in Column I...Ch. 2.4 - Concept Check Refer to the discussion of accuracy...Ch. 2.4 - Mt. Everest When Mt. Everest was first surveyed,...Ch. 2.4 - 9. Vehicular Tunnel The E. Johnson Memorial...Ch. 2.4 - WNBA Scorer Womens National Basketball Association...Ch. 2.4 - 11. If h is the actual height of a building and...Ch. 2.4 - If w is the actual weight of a car and the weight...Ch. 2.4 - Solve each right triangle. When two sides are...Ch. 2.4 - Solve each right triangle. When two sides are...Ch. 2.4 - Solve each right triangle. When two sides are...Ch. 2.4 - Solve each right triangle. When two sides are...Ch. 2.4 - Solve each right triangle. When two sides are...Ch. 2.4 - Solve each right triangle. When two sides are...Ch. 2.4 - Solve each right triangle. When two sides are...Ch. 2.4 - Solve each right triangle. When two sides are...Ch. 2.4 - 21. Can a right triangle be solved if we are...Ch. 2.4 - If we are given an acute angle and a side in a...Ch. 2.4 - Why can we always solve a right triangle if we...Ch. 2.4 - 24. Why can we always solve a right triangle if...Ch. 2.4 - Solve each right triangle. In each case, C = 90....Ch. 2.4 - Solve each right triangle. In each case, C = 90°....Ch. 2.4 - Solve each right triangle. In each case, C = 90....Ch. 2.4 - Solve each right triangle. In each case, C = 90....Ch. 2.4 - Solve each right triangle. In each case, C = 90....Ch. 2.4 - Solve each right triangle. In each case, C =...Ch. 2.4 - Solve each right triangle. In each case, C =...Ch. 2.4 - Solve each right triangle. In each case, C = 90....Ch. 2.4 - Solve each right triangle. In each case, C = 90....Ch. 2.4 - Solve each right triangle. In each case, C = 90....Ch. 2.4 - Solve each right triangle. In each case, C = 90....Ch. 2.4 - Solve each right triangle. In each case, C = 90°....Ch. 2.4 - Solve each right triangle. In each case, C = 90....Ch. 2.4 - Prob. 38ECh. 2.4 - Solve each right triangle. In each case, C =...Ch. 2.4 - Prob. 40ECh. 2.4 - What is the meaning of the term angle of...Ch. 2.4 - Prob. 42ECh. 2.4 - Why does the angle of depression DAB in the figure...Ch. 2.4 - Concept CheckAnswer each question. Why is angle...Ch. 2.4 - Solve each problem. See Examples 14. Height of a...Ch. 2.4 - Distance across a Lake To find the distance RS...Ch. 2.4 - Height of a Building From a window 30.0 ft above...Ch. 2.4 - Diameter of the Sun To determine the diameter of...Ch. 2.4 - 49. Side lengths of a Triangle The length of the...Ch. 2.4 - Altitude of a Triangle Find the altitude of an...Ch. 2.4 - Solve each problem. See Examples 3 and 4. 51....Ch. 2.4 - 52. Distance from the Ground to the Top of a...Ch. 2.4 - Length of a Shadow Suppose that the angle of...Ch. 2.4 - 54. Airplane Distance An airplane is flying...Ch. 2.4 - 55. Angle of Depression of a Light A company...Ch. 2.4 - Height of a Building The angle of elevation from...Ch. 2.4 - 57. Angle of Elevation of the Sun The length of...Ch. 2.4 - Prob. 58ECh. 2.4 - Angle of Elevation of the Pyramid of the Sun The...Ch. 2.4 - Cloud Ceiling The U.S. Weather Bureau defines a...Ch. 2.4 - 61. Height of Mt. Everest The highest mountain...Ch. 2.4 - 62. Error in Measurement A degree may seem like a...Ch. 2.5 - CONCEPT PREVIEW Match the measure of bearing in...Ch. 2.5 - CONCEPT PREVIEW Match the measure of bearing in...Ch. 2.5 - CONCEPT PREVIEW Match the measure of bearing in...Ch. 2.5 - Prob. 4ECh. 2.5 - CONCEPT PREVIEW Match the measure of bearing in...Ch. 2.5 - CONCEPT PREVIEW Match the measure of bearing in...Ch. 2.5 - CONCEPT PREVIEW Match the measure of bearing in...Ch. 2.5 - CONCEPT PREVIEW Match the measure of bearing in...Ch. 2.5 - CONCEPT PREVIEW Match the measure of bearing in...Ch. 2.5 - CONCEPT PREVIEW Match the measure of bearing in...Ch. 2.5 - Prob. 11ECh. 2.5 - The two methods of expressing bearing can be...Ch. 2.5 - The two methods of expressing bearing can be...Ch. 2.5 - Prob. 14ECh. 2.5 - Prob. 15ECh. 2.5 - Prob. 16ECh. 2.5 - Prob. 17ECh. 2.5 - The two methods of expressing bearing can be...Ch. 2.5 - Distance Flown by a Plane A plane flies 1.3 hr at...Ch. 2.5 - 20. Distance Traveled by a Ship A ship travels 55...Ch. 2.5 - Distance between Two Ships Two ships leave a port...Ch. 2.5 - 22. Distance between Two Ships Two ships leave a...Ch. 2.5 - Distance between Two Docks Two docks are located...Ch. 2.5 - 24. Distance between Two Lighthouses Two...Ch. 2.5 - 25. Distance between Two Ships A ship leaves its...Ch. 2.5 - Distance between Transmitters Radio direction...Ch. 2.5 - 27. Flying Distance The bearing from A to C is S...Ch. 2.5 - Flying Distance The bearing from A to C is N 64 W....Ch. 2.5 - Distance between Two Cities The bearing from...Ch. 2.5 - Prob. 30ECh. 2.5 - 31. Height of a Pyramid The angle of elevation...Ch. 2.5 - Distance between a Whale and a Lighthouse A whale...Ch. 2.5 - Height of an Antenna A scanner antenna is on top...Ch. 2.5 - 34. Height of Mt. Whitney The angle of elevation...Ch. 2.5 - 35. Find h as indicated in the figure. Ch. 2.5 - Find h as indicated in the figure.Ch. 2.5 - Distance of a Plant from a Fence In one area, the...Ch. 2.5 - Prob. 38ECh. 2.5 - Height of a Plane above Harth Find the minimum...Ch. 2.5 - Length of a Side of a Piece of Land A piece of...Ch. 2.5 - 41. (Modeling) Distance between Two Points A...Ch. 2.5 - (Modeling) Distance of a Shot Put A shot-putter...Ch. 2.5 - (Modeling) Highway Curves A basic highway curve...Ch. 2.5 - 44. (Modeling) Stopping Distance on a Curve Refer...Ch. 2.5 - The figure to the right indicates that the...Ch. 2.5 - Prob. 46ECh. 2.5 - Show that a line bisecting the first and third...Ch. 2.5 - Prob. 48ECh. 2.5 - Prob. 49ECh. 2.5 - 50. Repeat Exercise 49 for a bearing of 150°. Ch. 2 - Find exact values of the six trigonometric...Ch. 2 - Find exact values of the six trigonometric...Ch. 2 - Find one solution for each equation. Assume that...Ch. 2 - Find one solution for each equation. Assume that...Ch. 2 - Find one solution for each equation. Assume that...Ch. 2 - Find one solution for each equation. Assume that...Ch. 2 - Determine whether each statement is true or false....Ch. 2 - Determine whether each statement is true or false....Ch. 2 - Determine whether each statement is true or false....Ch. 2 - Prob. 10RECh. 2 - Prob. 11RECh. 2 - 12. Which one of the following cannot be exactly...Ch. 2 - Find exact values of the six trigonometric...Ch. 2 - Find exact values of the six trigonometric...Ch. 2 - Find one solution for each equation. Assume that...Ch. 2 - Find exact values of the six trigonometric...Ch. 2 - Find all values of . if is in the interval [0....Ch. 2 - Prob. 18RECh. 2 - Prob. 19RECh. 2 - Find all values of . if is in the interval [0....Ch. 2 - Prob. 21RECh. 2 - Prob. 22RECh. 2 - Evaluate each expression. Give exact values. 23....Ch. 2 - Prob. 24RECh. 2 - Prob. 25RECh. 2 - Prob. 26RECh. 2 - Prob. 27RECh. 2 - Use a calculator to approximate the value of each...Ch. 2 - Prob. 29RECh. 2 - Use a calculator to approximate the value of each...Ch. 2 - Use a calculator to find each value of θ, where θ...Ch. 2 - Use a calculator to find each value of θ, where θ...Ch. 2 - Prob. 33RECh. 2 - Use a calculator to find each value of , where is...Ch. 2 - Prob. 35RECh. 2 - Prob. 36RECh. 2 - Prob. 37RECh. 2 - Find two angles in the internal [0o, 360] that...Ch. 2 - Prob. 39RECh. 2 - Prob. 40RECh. 2 - Prob. 41RECh. 2 - Determine whether each statement is true or...Ch. 2 - Prob. 43RECh. 2 - Prob. 44RECh. 2 - Prob. 45RECh. 2 - Prob. 46RECh. 2 - Prob. 47RECh. 2 - Solve each right triangle. In Exercise 46, give...Ch. 2 - Prob. 49RECh. 2 - Prob. 50RECh. 2 - Prob. 51RECh. 2 - Height of a Tower The angle of depression from a...Ch. 2 - Prob. 53RECh. 2 - Prob. 54RECh. 2 - Prob. 55RECh. 2 - 56. Distance a Ship Sails The bearing from point...Ch. 2 - Prob. 57RECh. 2 - 58. Find a formula for h in term of k, A, and B....Ch. 2 - Prob. 59RECh. 2 - Prob. 60RECh. 2 - Prob. 61RECh. 2 - Prob. 62RECh. 2 - Prob. 1TCh. 2 - Prob. 2TCh. 2 - Prob. 3TCh. 2 - Prob. 4TCh. 2 - Prob. 5TCh. 2 - Prob. 6TCh. 2 - Prob. 7TCh. 2 - Prob. 8TCh. 2 - Prob. 9TCh. 2 - Prob. 10TCh. 2 - Prob. 11TCh. 2 - Prob. 12TCh. 2 - Prob. 13TCh. 2 - Prob. 14TCh. 2 - 15. Antenna Mast Guy Wire A guy wire 77.4 m long...Ch. 2 - Height of a Flagpole To measure the height of a...Ch. 2 - Altitude of a Mountain The highest point in Texas...Ch. 2 - Distance between Two Points Two ships leave a port...Ch. 2 - Prob. 19TCh. 2 - Find h as indicated in the figure.
Knowledge Booster
Background pattern image
Trigonometry
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, trigonometry and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Elementary Algebra
Algebra
ISBN:9780998625713
Author:Lynn Marecek, MaryAnne Anthony-Smith
Publisher:OpenStax - Rice University
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Text book image
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Text book image
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
SEE MORE TEXTBOOKS
What are the Different Types of Triangles? | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=1k0G-Y41jRA;License: Standard YouTube License, CC-BY
Law of Sines AAS, ASA, SSA Ambiguous Case; Author: Mario's Math Tutoring;https://www.youtube.com/watch?v=FPVGb-yWj3s;License: Standard YouTube License, CC-BY
Introduction to Statistics..What are they? And, How Do I Know Which One to Choose?; Author: The Doctoral Journey;https://www.youtube.com/watch?v=HpyRybBEDQ0;License: Standard YouTube License, CC-BY
Triangles | Mathematics Grade 5 | Periwinkle; Author: Periwinkle;https://www.youtube.com/watch?v=zneP1Q7IjgQ;License: Standard YouTube License, CC-BY
What Are Descriptive Statistics And Inferential Statistics?; Author: Amour Learning;https://www.youtube.com/watch?v=MUyUaouisZE;License: Standard Youtube License