Finite Mathematics & Its Applications (12th Edition)
12th Edition
ISBN: 9780134507125
Author: Goldstein
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 2.1, Problem 70E
College Majors The bar graph in Fig. 6 gives the intended majors of a group of 100 randomly selected college freshmen. (The biology category includes the biological and life sciences.) Six more students intend to major in biology than intend to major in business. The number of students intending to major in fields other than business or biology is 4 more than twice the number of students majoring in business or biology. Let x, y, and z represent the three numbers shown in the figure. Use the methods of this section to determine the values of x, y, and z.
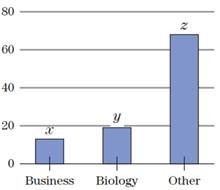
Figure 6 Intended Majors
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Directions: For problems 1 through 3, read each question carefully and be sure to show all work.
1. What is the phase shift for y = 2sin(2x-)?
2. What is the amplitude of y = 7cos(2x+л)?
3. What is the period of y = sin(3x-π)?
Directions: For problems 4 and 5, you were to compare and contrast the two functions in each problem situation. Be sure to
include a discussion of similarities and differences for the periods, amplitudes, y-minimums, y-maximums, and any phase shift
between the two graphs. Write in complete sentences.
4. y 3sin(2x) and y = 3cos(2x)
5. y 4sin(2x) and y = cos(3x- -플)
A graph G of order 12 has vertex set V(G) = {c1, c2, …, c12} for the twelve configurations inFigure 1.4. A “move” on this checkerboard corresponds to moving a single coin to anunoccupied square, where(1) the gold coin can only be moved horizontally or diagonally,(2) the silver coin can only be moved vertically or diagonally.Two vertices ci and cj (i ≠ j) are adjacent if it is possible to move ci to cj by a single move.
(a) What vertices are adjacent to c1 in G?(c) Draw the subgraph of G induced by {c2, c6, c9, c11}.
i) Consider the set S = {−6, −3, 0, 3, 6}. Draw a graph G whose set of verti-
ces be S and such that for i, j ∈ S, ij ∈ E(G) if ij are related to a rule that t'u
you choose to apply to i and j.
(ii) A graph G of order 12 has as a set of vertices c1, c2, . . . , c12 for the do-
ce configurations of figure 1. A movement on said board corresponds to moving a
coin to an unoccupied square using the following two rules:
1. the gold coin can move only horizontally or diagonally,
2. the silver coin can move only vertically or diagonally.
Two vertices ci, cj, i̸ = j are adjacent if it is possible to move ci to cj in a single movement.
a) What vertices are adjacent to c1 in G?
b) Draw the subgraph induced by {c2, c6, c9, c11}
Chapter 2 Solutions
Finite Mathematics & Its Applications (12th Edition)
Ch. 2.1 - 1. Determine whether the following systems of...Ch. 2.1 - Give the meaning of each of the following...Ch. 2.1 - 3. Perform the indicated elementary row...Ch. 2.1 - State the next elementary row operation that...Ch. 2.1 - In Exercises 1–8, perform the indicated elementary...Ch. 2.1 - Prob. 2ECh. 2.1 - In Exercises 1–8, perform the indicated elementary...Ch. 2.1 - In Exercises 1–8, perform the indicated elementary...Ch. 2.1 - In Exercises 18, perform the indicated elementary...Ch. 2.1 - In Exercises 18, perform the indicated elementary...
Ch. 2.1 - In Exercises 18, perform the indicated elementary...Ch. 2.1 - In Exercises 1–8, perform the indicated elementary...Ch. 2.1 - In Exercises 9–12, write the augmented matrix...Ch. 2.1 - In Exercises 912, write the augmented matrix...Ch. 2.1 - In Exercises 9–12, write the augmented matrix...Ch. 2.1 - In Exercises 912, write the augmented matrix...Ch. 2.1 - In Exercises 13–16, write the system of linear...Ch. 2.1 - In Exercises 1316, write the system of linear...Ch. 2.1 - In Exercises 1316, write the system of linear...Ch. 2.1 - In Exercises 1316, write the system of linear...Ch. 2.1 - In Exercises 17–22, describe in your own words the...Ch. 2.1 - In Exercises 17–22, describe in your own words the...Ch. 2.1 - In Exercises 17–22, describe in your own words the...Ch. 2.1 - In Exercises 1722, describe in your own words the...Ch. 2.1 - In Exercises 1722, describe in your own words the...Ch. 2.1 - In Exercises 17–22, describe in your own words the...Ch. 2.1 - In Exercises 2328, carry out the indicated...Ch. 2.1 - In Exercises 2328, carry out the indicated...Ch. 2.1 - In Exercises 23–28, carry out the indicated...Ch. 2.1 - In Exercises 2328, carry out the indicated...Ch. 2.1 - In Exercises 2328, carry out the indicated...Ch. 2.1 - In Exercises 2328, carry out the indicated...Ch. 2.1 - In Exercises 2936, state the next elementary row...Ch. 2.1 - In Exercises 29–36, state the next elementary row...Ch. 2.1 - In Exercises 29–36, state the next elementary row...Ch. 2.1 - Prob. 32ECh. 2.1 - In Exercises 29–36, state the next elementary row...Ch. 2.1 - In Exercises 29–36, state the next elementary row...Ch. 2.1 - In Exercises 29–36, state the next elementary row...Ch. 2.1 - Prob. 36ECh. 2.1 - In Exercises 37 and 38, two steps of the...Ch. 2.1 - In Exercises 37 and 38, two steps of the...Ch. 2.1 - The screen captures in Exercises 3946 show a...Ch. 2.1 - Prob. 40ECh. 2.1 - The screen captures in Exercises 3946 show a...Ch. 2.1 - Prob. 42ECh. 2.1 - The screen captures in Exercises 39–46 show a...Ch. 2.1 - Prob. 44ECh. 2.1 - The screen captures in Exercises 39–46 show a...Ch. 2.1 - The screen captures in Exercises 39–46 show a...Ch. 2.1 - In Exercises 47-60, solve the linear system by the...Ch. 2.1 - In Exercises 47-60, solve the linear system by the...Ch. 2.1 - In Exercises 47-60, solve the linear system by the...Ch. 2.1 - In Exercises 47-60, solve the linear system by the...Ch. 2.1 - In Exercises 47-60, solve the linear system by the...Ch. 2.1 - In Exercises 47-60, solve the linear system by the...Ch. 2.1 - In Exercises 47-60, solve the linear system by the...Ch. 2.1 - In Exercises 47-60, solve the linear system by the...Ch. 2.1 - In Exercises 47-60, solve the linear system by the...Ch. 2.1 - In Exercises 47-60, solve the linear system by the...Ch. 2.1 - In Exercises 47-60, solve the linear system by the...Ch. 2.1 - In Exercises 47-60, solve the linear system by the...Ch. 2.1 - In Exercises 47-60, solve the linear system by the...Ch. 2.1 - In Exercises 47-60, solve the linear system by the...Ch. 2.1 - A baked potato smothered with cheddar cheese...Ch. 2.1 - A high school math department purchased brand A...Ch. 2.1 - Exercises 63 and 64 are multiple choice exercises...Ch. 2.1 - Exercises 63 and 64 are multiple choice exercises...Ch. 2.1 - Sales A street vendor has a total of 350 short-...Ch. 2.1 - Sales A grocery store carries two brands of...Ch. 2.1 - Movie tickets A 275-seat movie theater charges...Ch. 2.1 - Batting average A baseball players batting average...Ch. 2.1 - 69. Areas of countries The United States and...Ch. 2.1 - College Majors The bar graph in Fig. 6 gives the...Ch. 2.1 - Coffee Blends A one-pound blend of coffee uses...Ch. 2.1 - 72. Nut Mixture A one-pound mixture of nuts...Ch. 2.1 - 73. Investment planning A bank wishes to invest a...Ch. 2.1 - Nutrition planning A dietitian wishes to plan a...Ch. 2.1 - Prob. 75ECh. 2.1 - Prob. 76ECh. 2.1 - In Exercises 77–80, use technology to put the...Ch. 2.1 - Prob. 78ECh. 2.1 - Prob. 79ECh. 2.1 - Prob. 80ECh. 2.1 - Prob. 81ECh. 2.1 - Prob. 82ECh. 2.1 - Prob. 83ECh. 2.1 - Prob. 84ECh. 2.2 - Find a specific solution to a system of linear...Ch. 2.2 - 2. Find all solutions of this system of linear...Ch. 2.2 - In Exercises 1–8, pivot the matrix about the...Ch. 2.2 - In Exercises 1–8, pivot the matrix about the...Ch. 2.2 - In Exercises 1–8, pivot the matrix about the...Ch. 2.2 - In Exercises 1–8, pivot the matrix about the...Ch. 2.2 - In Exercises 1–8, pivot the matrix about the...Ch. 2.2 - In Exercises 1–8, pivot the matrix about the...Ch. 2.2 - In Exercises 18, pivot the matrix about the...Ch. 2.2 - In Exercises 18, pivot the matrix about the...Ch. 2.2 - The screen captures in Exercises 9–16 show a...Ch. 2.2 - The screen captures in Exercises 9–16 show a...Ch. 2.2 - The screen captures in Exercises 916 show a...Ch. 2.2 - The screen captures in Exercises 916 show a...Ch. 2.2 - The screen captures in Exercises 916 show a...Ch. 2.2 - The screen captures in Exercises 9–16 show a...Ch. 2.2 - Prob. 15ECh. 2.2 - Prob. 16ECh. 2.2 - In Exercise 1736, use the Gauss-Jordan elimination...Ch. 2.2 - In Exercise 1736, use the Gauss-Jordan elimination...Ch. 2.2 - In Exercise 1736, use the Gauss-Jordan elimination...Ch. 2.2 - In Exercise 1736, use the Gauss-Jordan elimination...Ch. 2.2 - In Exercise 1736, use the Gauss-Jordan elimination...Ch. 2.2 - In Exercise 17–36, use the Gauss-Jordan...Ch. 2.2 - In Exercise 17–36, use the Gauss-Jordan...Ch. 2.2 - In Exercise 1736, use the Gauss-Jordan elimination...Ch. 2.2 - In Exercise 17–36, use the Gauss-Jordan...Ch. 2.2 - In Exercise 17–36, use the Gauss-Jordan...Ch. 2.2 - In Exercise 1736, use the Gauss-Jordan elimination...Ch. 2.2 - In Exercise 17–36, use the Gauss-Jordan...Ch. 2.2 - In Exercise 17–36, use the Gauss-Jordan...Ch. 2.2 - In Exercise 17–36, use the Gauss-Jordan...Ch. 2.2 - Prob. 31ECh. 2.2 - In Exercise 17–36, use the Gauss-Jordan...Ch. 2.2 - In Exercise 1736, use the Gauss-Jordan elimination...Ch. 2.2 - In Exercise 1736, use the Gauss-Jordan elimination...Ch. 2.2 - In Exercise 17–36, use the Gauss-Jordan...Ch. 2.2 - Prob. 36ECh. 2.2 - In Exercises 37–40, find three solutions to the...Ch. 2.2 - In Exercises 37–40, find three solutions to the...Ch. 2.2 - In Exercises 3740, find three solutions to the...Ch. 2.2 - In Exercises 37–40, find three solutions to the...Ch. 2.2 - 41. Nutrition planning In a laboratory experiment,...Ch. 2.2 - Nutrition planning Rework Exercise 41 with the...Ch. 2.2 - Nutrition planning The nutritional content of...Ch. 2.2 - 44. Nutrition planning Refer to Exercise 43. Show...Ch. 2.2 - Furniture Manufacturing A furniture manufacturer...Ch. 2.2 - Computer equipment An office manager placed an...Ch. 2.2 - 47. Quilting Granny’s Custom Quilts receives an...Ch. 2.2 - 48. Purchasing Options Amanda is decorating her...Ch. 2.2 - 49. For what values(s) of k will the following...Ch. 2.2 - For what value of k will the following system of...Ch. 2.2 - Figure 5 shows the graphs of the equations from a...Ch. 2.2 - Prob. 52ECh. 2.2 - In Exercises 53–56, graph the three equations...Ch. 2.2 - Prob. 54ECh. 2.2 - Prob. 55ECh. 2.2 - Prob. 56ECh. 2.2 - Apply rref or row reduce to the matrix in Example...Ch. 2.2 - Prob. 58ECh. 2.3 - Compute [3121012041][710542604].Ch. 2.3 - 2. Give the system of linear equations that is...Ch. 2.3 - Give a matrix equation equivalent to this system...Ch. 2.3 - In Exercises 16, give the size and special...Ch. 2.3 - Prob. 2ECh. 2.3 - In Exercises 16, give the size and special...Ch. 2.3 - Prob. 4ECh. 2.3 - In Exercises 16, give the size and special...Ch. 2.3 - In Exercises 1–6, give the size and special...Ch. 2.3 - Exercises 7–10 refer to the matrix .
7. Find and...Ch. 2.3 - Exercises 710 refer to the 23 matrix A=[246031]....Ch. 2.3 - Exercises 710 refer to the 23 matrix A=[246031]....Ch. 2.3 - Exercises 7–10 refer to the matrix .
10. For what...Ch. 2.3 - In Exercises 11-26, perform the indicated matrix...Ch. 2.3 - In Exercises 11-26, perform the indicated matrix...Ch. 2.3 - In Exercises 11-26, perform the indicated matrix...Ch. 2.3 - In Exercises 11-26, perform the indicated matrix...Ch. 2.3 - In Exercises 11-26, perform the indicated matrix...Ch. 2.3 - In Exercises 11-26, perform the indicated matrix...Ch. 2.3 - In Exercises 11-26, perform the indicated matrix...Ch. 2.3 - In Exercises 11-26, perform the indicated matrix...Ch. 2.3 - In Exercises 11-26, perform the indicated matrix...Ch. 2.3 - In Exercises 11-26, perform the indicated matrix...Ch. 2.3 - In Exercises 11-26, perform the indicated matrix...Ch. 2.3 - In Exercises 11-26, perform the indicated matrix...Ch. 2.3 - In Exercises 11-26, perform the indicated matrix...Ch. 2.3 - In Exercises 11-26, perform the indicated matrix...Ch. 2.3 - In Exercises 11-26, perform the indicated matrix...Ch. 2.3 - In Exercises 11-26, perform the indicated matrix...Ch. 2.3 - In Exercises 27–32, the sizes of two matrices are...Ch. 2.3 - In Exercises 27–32, the sizes of two matrices are...Ch. 2.3 - In Exercises 27–32, the sizes of two matrices are...Ch. 2.3 - In Exercises 27–32, the sizes of two matrices are...Ch. 2.3 - In Exercises 27–32, the sizes of two matrices are...Ch. 2.3 - In Exercises 2732, the sizes of two matrices are...Ch. 2.3 - In Exercises 33-52, perform the...Ch. 2.3 - In Exercises 33-52, perform the multiplication....Ch. 2.3 - In Exercises 33-52, perform the multiplication....Ch. 2.3 - In Exercises 33-52, perform the multiplication....Ch. 2.3 - In Exercises 33-52, perform the...Ch. 2.3 - In Exercises 33-52, perform the multiplication....Ch. 2.3 - In Exercises 33-52, perform the...Ch. 2.3 - In Exercises 33-52, perform the multiplication....Ch. 2.3 - In Exercises 33-52, perform the multiplication....Ch. 2.3 - In Exercises 33-52, perform the...Ch. 2.3 - In Exercises 33-52, perform the multiplication....Ch. 2.3 - Prob. 44ECh. 2.3 - In Exercises 33-52, perform the multiplication....Ch. 2.3 - In Exercises 33-52, perform the...Ch. 2.3 - Prob. 47ECh. 2.3 - Prob. 48ECh. 2.3 - Prob. 49ECh. 2.3 - In Exercises 33-52, perform the multiplication....Ch. 2.3 - In Exercises 33-52, perform the...Ch. 2.3 - In Exercises 33-52, perform the...Ch. 2.3 - In Exercises 53-56, give the system of linear...Ch. 2.3 - In Exercises 53-56, give the system of linear...Ch. 2.3 - In Exercises 53-56, give the system of linear...Ch. 2.3 - In Exercises 53-56, give the system of linear...Ch. 2.3 - In Exercises 5760, write the given system of...Ch. 2.3 - In Exercises 57–60, write the given system of...Ch. 2.3 - In Exercises 57–60, write the given system of...Ch. 2.3 - In Exercises 57–60, write the given system of...Ch. 2.3 - Prob. 61ECh. 2.3 - Prob. 62ECh. 2.3 - Prob. 63ECh. 2.3 - Prob. 64ECh. 2.3 - Wardrobe costs The quantities of pants, shirts,...Ch. 2.3 - Retail Sales Two stores sell the exact same brand...Ch. 2.3 - Retail Sales A candy shop sells various items for...Ch. 2.3 - Wholesale and retail Sales A company has three...Ch. 2.3 - Prob. 69ECh. 2.3 - 70. Semester Grades A professor bases semester...Ch. 2.3 - Prob. 71ECh. 2.3 - Prob. 72ECh. 2.3 - 73. Labor Costs Suppose that a contractor employs...Ch. 2.3 - Prob. 74ECh. 2.3 - Nutrition Analysis Mikeys diet consists of food X...Ch. 2.3 - Bakery Sales A bakery makes three types of...Ch. 2.3 - Revenue A community fitness center has a pool and...Ch. 2.3 - Prob. 78ECh. 2.3 - 79. Production Planning A bakery sells Boston...Ch. 2.3 - Prob. 80ECh. 2.3 - Prob. 81ECh. 2.3 - MP3 Sales A store sells three types of MP3...Ch. 2.3 - Prob. 83ECh. 2.3 - Prob. 84ECh. 2.3 - Prob. 85ECh. 2.3 - Prob. 86ECh. 2.3 - Prob. 87ECh. 2.3 - Prob. 88ECh. 2.3 - Prob. 89ECh. 2.3 - Prob. 90ECh. 2.3 - Prob. 91ECh. 2.3 - Prob. 92ECh. 2.3 - Prob. 93ECh. 2.3 - Prob. 94ECh. 2.3 - Prob. 95ECh. 2.3 - Prob. 96ECh. 2.3 - Prob. 97ECh. 2.3 - Prob. 98ECh. 2.4 - Show that the inverse of...Ch. 2.4 - 2. Use the method of this section to solve the...Ch. 2.4 - In Exercises 1 and 2, use the fact that...Ch. 2.4 - In Exercises 1 and 2, use the fact that...Ch. 2.4 - In Exercises 310, find the inverse of the given...Ch. 2.4 - In Exercises 310, find the inverse of the given...Ch. 2.4 - In Exercises 3–10, find the inverse of the given...Ch. 2.4 - In Exercises 3–10, find the inverse of the given...Ch. 2.4 - In Exercises 3–10, find the inverse of the given...Ch. 2.4 - In Exercises 3–10, find the inverse of the given...Ch. 2.4 - In Exercises 3–10, find the inverse of the given...Ch. 2.4 - In Exercises 310, find the inverse of the given...Ch. 2.4 - In Exercises 11–14, use a matrix equation to solve...Ch. 2.4 - In Exercises 1114, use a matrix equation to solve...Ch. 2.4 - In Exercises 1114, use a matrix equation to solve...Ch. 2.4 - In Exercises 1114, use a matrix equation to solve...Ch. 2.4 - Marriage Trends It is found that the number of...Ch. 2.4 - Epidemiology A flu epidemic is spreading through a...Ch. 2.4 - 17. Housing Trends Statistics show that, at a...Ch. 2.4 - Performance on Tests A teacher estimates that, of...Ch. 2.4 - In Exercises 19–22, use the fact that the...Ch. 2.4 - In Exercises 19–22, use the fact that the...Ch. 2.4 - In Exercises 19–22, use the fact that the...Ch. 2.4 - In Exercises 19–22, use the fact that the...Ch. 2.4 - In Exercises 23–26, use the fact that the...Ch. 2.4 - In Exercises 2326, use the fact that the following...Ch. 2.4 - In Exercises 23–26, use the fact that the...Ch. 2.4 - In Exercises 2326, use the fact that the following...Ch. 2.4 - 27. Show that if and , then the inverse of is...Ch. 2.4 - (True or False) If B is the inverse of A, then A...Ch. 2.4 - Prob. 29ECh. 2.4 - 30. If and , what is A?
Ch. 2.4 - 31. Show that, if AB is a matrix of all zeros and...Ch. 2.4 - Consider the matrices A=[3152] and B=[6252]. Show...Ch. 2.4 - Find a 22 matrix A and a 21 column matrix B for...Ch. 2.4 - 34. Find a matrix A and a column matrix B for...Ch. 2.4 - In Exercises 3538, use the inverse operation to...Ch. 2.4 - In Exercises 35–38, use the inverse operation to...Ch. 2.4 - In Exercises 35–38, use the inverse operation to...Ch. 2.4 - In Exercises 35–38, use the inverse operation to...Ch. 2.4 - In Exercises 3942, calculate the solution by using...Ch. 2.4 - In Exercises 39–42, calculate the solution by...Ch. 2.4 - In Exercises 3942, calculate the solution by using...Ch. 2.4 - In Exercises 39–42, calculate the solution by...Ch. 2.4 - 43. Try finding the inverse of a matrix that does...Ch. 2.5 - 1. Use the Gauss–Jordan method to calculate the...Ch. 2.5 - Solve the system of linear equations...Ch. 2.5 - In Exercises 1–12, use the Gauss–Jordan method to...Ch. 2.5 - In Exercises 1–12, use the Gauss–Jordan method to...Ch. 2.5 - In Exercises 1–12, use the Gauss–Jordan method to...Ch. 2.5 - In Exercises 1–12, use the Gauss–Jordan method to...Ch. 2.5 - In Exercises 1–12, use the Gauss–Jordan method to...Ch. 2.5 - In Exercises 1–12, use the Gauss–Jordan method to...Ch. 2.5 - In Exercises 112, use the GaussJordan method to...Ch. 2.5 - In Exercises 1–12, use the Gauss–Jordan method to...Ch. 2.5 - In Exercises 112, use the GaussJordan method to...Ch. 2.5 - In Exercises 112, use the GaussJordan method to...Ch. 2.5 - In Exercises 112, use the GaussJordan method to...Ch. 2.5 - In Exercises 1–12, use the Gauss–Jordan method to...Ch. 2.5 - In Exercises 13–18, use an inverse matrix to solve...Ch. 2.5 - In Exercises 13–18, use an inverse matrix to solve...Ch. 2.5 - In Exercises 1318, use an inverse matrix to solve...Ch. 2.5 - In Exercises 13–18, use an inverse matrix to solve...Ch. 2.5 - In Exercises 13–18, use an inverse matrix to solve...Ch. 2.5 - In Exercises 1318, use an inverse matrix to solve...Ch. 2.5 - 19. Find a matrix A for which
.
Ch. 2.5 - Find a 22 matrix A for which [2513]A=[1042].Ch. 2.5 - College Degrees Figure 1 gives the responses of a...Ch. 2.5 - 22. College Choices Figure 2 gives the responses...Ch. 2.5 - 23. High School attended Figure 3 gives the...Ch. 2.5 - Placement Tests Figure 4 gives the responses of a...Ch. 2.6 - Let...Ch. 2.6 - Prob. 2CYUCh. 2.6 - Prob. 1ECh. 2.6 - Prob. 2ECh. 2.6 - Prob. 3ECh. 2.6 - Prob. 4ECh. 2.6 - Prob. 5ECh. 2.6 - Prob. 6ECh. 2.6 - Prob. 7ECh. 2.6 - Prob. 8ECh. 2.6 - Prob. 9ECh. 2.6 - Prob. 10ECh. 2.6 - Prob. 11ECh. 2.6 - Three-Sector Economy In Exercises 112, suppose...Ch. 2.6 - 13. Industrial Production Suppose that, in the...Ch. 2.6 - Conglomerate Suppose that the conglomerate of...Ch. 2.6 - Prob. 15ECh. 2.6 - 16. Industrial Production Suppose that the economy...Ch. 2.6 - Industrial Production In the economy of Example 1,...Ch. 2.6 - Prob. 18ECh. 2.6 - Prob. 19ECh. 2.6 - Prob. 20ECh. 2.6 - Prob. 21ECh. 2.6 - Prob. 22ECh. 2.6 - Prob. 23ECh. 2.6 - Prob. 24ECh. 2.6 - Prob. 25ECh. 2.6 - Three-Sector Economy An economy consists of the...Ch. 2.6 - 27. Localized Economy A town has a merchant, a...Ch. 2.6 - Prob. 28ECh. 2.6 - Prob. 29ECh. 2.6 - Prob. 30ECh. 2.6 - Prob. 31ECh. 2.6 - Prob. 32ECh. 2 - What is meant by a solution to a system of linear...Ch. 2 - What is a matrix?Ch. 2 - 3. State the three elementary row operations on...Ch. 2 - Prob. 4FCCECh. 2 - What is meant by pivoting a matrix about a nonzero...Ch. 2 - 6. State the Gauss–Jordan elimination method for...Ch. 2 - 7. What is a row matrix? Column matrix? Square...Ch. 2 - Prob. 8FCCECh. 2 - Define the sum and difference of two matrices.Ch. 2 - Define the product of two matrices.Ch. 2 - Prob. 11FCCECh. 2 - Prob. 12FCCECh. 2 - Prob. 13FCCECh. 2 - 14. Explain how to use the inverse of a matrix to...Ch. 2 - Prob. 15FCCECh. 2 - Prob. 16FCCECh. 2 - Prob. 17FCCECh. 2 - Prob. 1RECh. 2 - Prob. 2RECh. 2 - Prob. 3RECh. 2 - In Exercises 3–8, use the Gauss–Jordan elimination...Ch. 2 - Prob. 5RECh. 2 - Prob. 6RECh. 2 - Prob. 7RECh. 2 - Prob. 8RECh. 2 - Prob. 9RECh. 2 - Prob. 10RECh. 2 - Prob. 11RECh. 2 - Prob. 12RECh. 2 - Prob. 13RECh. 2 - Prob. 14RECh. 2 - Prob. 15RECh. 2 - Prob. 16RECh. 2 - Prob. 17RECh. 2 - Prob. 18RECh. 2 - Crop Allocation Farmer Brown has 1000 acres of...Ch. 2 - Equipment Sales A company makes backyard...Ch. 2 - Prob. 21RECh. 2 - 22. Job Earnings Sara, Quinn, Tamia, and Zack are...Ch. 2 - Prob. 23RECh. 2 - Prob. 24RECh. 2 - Two-Sector Economy The economy of a small country...Ch. 2 - Coins Joe has $3.30 in his pocket, made up of...Ch. 2 - Identify each statement as true or false. (a) If a...Ch. 2 - Identify each statement as true or false. (a)...Ch. 2 - Prob. 29RECh. 2 - Prob. 30RECh. 2 - Prob. 31RECh. 2 - Prob. 32RECh. 2 - Prob. 33RECh. 2 - Population Dynamics In 1991, the U.S. Fish and...Ch. 2 - Population Dynamics In 1991, the U.S. Fish and...Ch. 2 - Population Dynamics In 1991, the U.S. Fish and...Ch. 2 - Prob. 4PCh. 2 - Prob. 5PCh. 2 - Prob. 6PCh. 2 - Prob. 7PCh. 2 - Prob. 8P
Additional Math Textbook Solutions
Find more solutions based on key concepts
1. How much money is Joe earning when he’s 30?
Pathways To Math Literacy (looseleaf)
Let F be a continuous distribution function. If U is uniformly distributed on (0,1), find the distribution func...
A First Course in Probability (10th Edition)
In Exercises 5-36, express all probabilities as fractions.
23. Combination Lock The typical combination lock us...
Elementary Statistics
First Derivative Test a. Locale the critical points of f. b. Use the First Derivative Test to locale the local ...
Calculus: Early Transcendentals (2nd Edition)
For Problems 23-28, write in simpler form, as in Example 4. logbFG
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Find how many SDs above the mean price would be predicted to cost.
Intro Stats, Books a la Carte Edition (5th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 2. Find the exact value of 12 + 12+12+√√12+ √12+ 12arrow_forwardhe following contingency table details the sex and age distribution of the patients currently registered at a family physician's medical practice. If the doctor sees 17 patients per day, use the binomial formula and the information contained in the table to answer the question: SEX AGE Under 20 20-39 40-59 60-79 80 or over TOTAL Male 5.6% 12.8% 18.4% 14.4% 3.6% 54.8% Female 2.8% 9.6% 13.2% 10.4% 9.2% 45.2% TOTAL 8.4% 22.4% 31.6% 24.8% 12.8% 100.0% if the doctor sees 6 male patients in a day, what is the probability that at most half of them are aged under 39?arrow_forwardTechnetium-99m is used as a radioactive tracer for certain medical tests. It has a half-life of 1 day. Consider the function TT where T(d)T(d) =100(2)−d=100(2)−d is the percent of Technetium-99m remaining dd days after the test. Which expression represents the number of days until only 5% remains?arrow_forward
- 1. Find the inverse of f(x) = = 2x 1+2x Then find the domain of the inverse.arrow_forwardProve for any graph G, δ(G) ≤ d(G) ≤ ∆(G) using the definition of average degree, make a formal proofarrow_forwardRestart box ixl.com/math/grade-6/area-of-compound-figures-with-triangles ass BModules Dashboard | Khan... Grades 6-8 Life S... t Typing Lessons BDashboard f IXL My IXL Learning Assessm Sixth grade >GG.12 Area of compound figures with triangles 5V2 What is the area of this figure? 4 km 2 km 5 km 4 km 2 km Learn with an example 13 km Write your answer using decimals, if necessary. square kilometers Submit Area of compound figures Area of triangles (74) Work it out Not feeling ready yet? Thesarrow_forward
- The diagonals of rhombus ABCD intersect at E. Given that BAC=53 degrees, DE=8, and EC=6 find AEarrow_forwardNot use ai pleasearrow_forward2. [-/4 Points] DETAILS MY NOTES SESSCALCET2 7.3.002. Let S be the solid obtained by rotating the region shown in the figure about the y-axis. (Assume a = 6 and b = 2.) ASK YOUR TEACHER 0 y = a sin(bx²) Sketch a typical approximating shell. y 6 4 2 x π/b y 2 1 x 0.5 1.0 1.5 0.2 0.4 0.6 0.8 1.0 -2 -1 -4arrow_forward
- Determine the volume and the surface area of the shape obtained by rotating the area of the figure about the x-axis and the y-axis.arrow_forwardI'm getting only chatgpt answer that are wrong Plz don't use chatgpt answer will upvote .arrow_forwardFind xyz cordinates of center of gravity given z = 3.47 inarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Sampling Methods and Bias with Surveys: Crash Course Statistics #10; Author: CrashCourse;https://www.youtube.com/watch?v=Rf-fIpB4D50;License: Standard YouTube License, CC-BY
Statistics: Sampling Methods; Author: Mathispower4u;https://www.youtube.com/watch?v=s6ApdTvgvOs;License: Standard YouTube License, CC-BY