Chapter 2.1, Problem 2.1P

Two forces are applied as shown to a hook. Determine graphically the magnitude and direction of their resultant using (a) the parallelogram law, (b) the triangle rule.

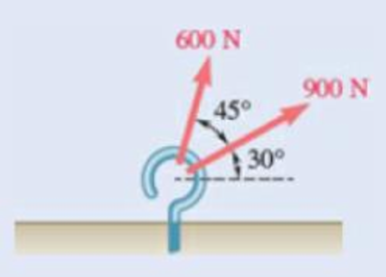
Fig. P2.1

To determine

The magnitude and direction of the resultant force on the hook graphically using the parallelogram law.

Answer to Problem 2.1P

The magnitude of the resultant force on the hook determined graphically using the parallelogram law is $1,391\text{ N}$ and it is at $47.8°$ with the horizontal.

Explanation of Solution

Force is a vector and the addition of vectors can be done using parallelogram law. The parallelogram law of vector addition says that if a parallelogram is constructed using two vectors by taking them as the adjacent sides of the parallelogram by attaching them on the same point, then the diagonal passing through that point gives the sum of the two vectors.

The forces acting on the hook are taken as the adjacent sides of the parallelogram. The diagram is shown in figure 1. In the figure, $\alpha$ is the angle the diagonal makes with the horizontal and $R$ is the resultant force.

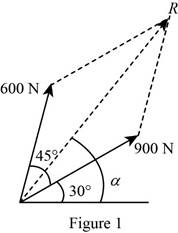
The length of the diagonal of the parallelogram gives the magnitude of the resultant vector and the angle the diagonal makes with the horizontal gives the direction.

Conclusion:

The length of the diagonal is measured to be $1,391\text{ N}$ and the value of $\alpha$ is found to be $47.8°$ .

Thus, the magnitude of the resultant force on the hook determined graphically using the parallelogram law is $1,391\text{ N}$ and it is at $47.8°$ with the horizontal.

To determine

The magnitude and direction of the resultant force on the hook graphically using the triangle rule.

Answer to Problem 2.1P

The magnitude of the resultant force on the hook determined graphically using the triangle rule is $1,391\text{ N}$ and it is at $47.8°$ with the horizontal.

Explanation of Solution

Force is a vector and one of the graphical methods to obtain the resultant of two vectors is triangle rule. The triangle rule says that the sum of two vectors can be found by arranging the vectors in tip-to-tail fashion and then connecting the tail of the first vector with the tip of the second.

The forces acting on the hook are arranged in tip-to-tail fashion by placing the tail of $900\text{ N}$ at the tip of $600\text{ N}$. The diagram is shown in figure 2. In the figure, $\alpha$ is the angle the resultant makes with the horizontal and $R$ is the resultant force.

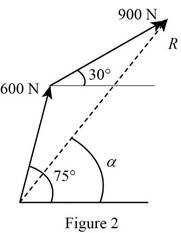
The length of the third side of the triangle formed gives the magnitude of the resultant force. The direction of the resultant force is specified by the angle the third side of the triangle makes with the horizontal.

Conclusion:

The length of the third side of the triangle is measured to be $1,391\text{ N}$ and the value of $\alpha$ is found to be $47.8°$.

Thus, the magnitude of the resultant force on the hook determined graphically using the triangle rule is $1,391\text{ N}$ and it is at $47.8°$ with the horizontal.