
Concept explainers
Figure 21-11 shows (1) four situations in which five charged particles are evenly spaced along an axis. The charge values are indicated except for the central particle, which has the same charge in all four situations. Rank the situations according to the magnitude of the net electrostatic force or the central particle, greatest first.
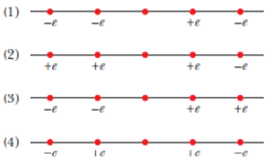
Figure 21-11 Question 1.
To rank:
The situations according to the magnitude of net electrostatic force exerted on the central particle by four given particles.
Answer to Problem 1Q
Solution:
Rank based on net electrostatic force is F3>F1>F2>F4
Explanation of Solution
1) Concept:
The net force acting on a particle due to more than one particle is the sum of forces exerted by each of the particles.
2) Formulae:
Electrostatic force between two charges q1 and q2,
k- Coulomb’s constant constant=8.99 x 109
d- distance of separation between particles.
3) Given:
a. The five particles are evenly spaced on an axis.
b. The charges on four particles are given except for the central particle.
Situation 1: Charges on right side = -e, -e Charges on left side =-+e, -e
Situation 2: Charges on right side = +e, +e Charges on left side =+e, -e
Situation 3: Charges on right side = -e, -e Charges on left side =+e, +e
Situation 4: Charges on right side = -e, +e Charges on left side =+e, -e
c. The central particle has same charge in all the 4 situations.
4) Calculation:
Let us consider that each of the particles is located at d distance apart.
Let us consider that the central particle has a charge +e.
According to Coulomb’s law, the magnitude of force F acting on the central particle due to the particles at distance d is,
Situation 1:
In the situation 1, the free body diagram of force acting on central particle, due to other particles is drawn as shown below.
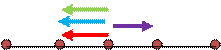 |
||||||||||||||||
|
|
|
|
|
||||||||||||
The particles located at distance 2d on either side, exert equal and opposite forces on the central particle. So they nullify each other’s effect on the central particle. Meanwhile, the particles at distance d exert equal forces towards the same direction, and hence the exerted forces add up to 2F.
Hence net force, F1= 2F
Situation 2:
|
|
|
|
|
||||||||||||
Force exerted by particles at distance d on either side nullifies each other. Hence, the net force on the central particle due to the particles at 2d distance,
F2 =
=
=
Situation 3:
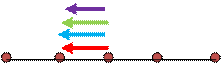 |
||||||||||||||||
|
|
|
|
|
||||||||||||
Here the particles at distance ‘d’ exert equal force on same direction as in situation 1. Hence the force exerted by these particles on central particle is 2F. The particles that are at 2d distance on either sides again exert same force in same direction as in situation 2. Hence the force exerted by them on central particle is 0.5F.
Net force, F3= F1+F2 = 2F +0.5 F = 2.5 F
Situation 4:
 |
||||||||||||||||
|
|
|
|
|
||||||||||||
Here the particles at distance ‘2d’ nullifies each other’s effect and also that are at distance ‘d’ again cancel the force exerted by each other. Therefore, the net force acting on the particle is zero.
Net force, F4=0
Conclusion:
We can find net electrostatic force acting on a particle by knowing the magnitude and direction of the forces exerted by each of the particles present in the system.
Want to see more full solutions like this?
Chapter 21 Solutions
FUND.OF PHYSICS(LL)-PRINT COMP-W/ACCESS
Additional Science Textbook Solutions
Biology: Life on Earth (11th Edition)
Campbell Biology (11th Edition)
Campbell Biology: Concepts & Connections (9th Edition)
Genetic Analysis: An Integrated Approach (3rd Edition)
Chemistry & Chemical Reactivity
Organic Chemistry (8th Edition)
- Lab 8 Part 3 PHET Wave Interface simulation. I am having trouble with this part of the lab.arrow_forwardMick and Rick are twins born on Earth in the year 2175. Rick grows up to be an Earth-bound robotics technician while Mick becomes an intergalactic astronaut. Mick leaves the Earth on his first space mission in the year 2200 and travels, according to his clock, for 10 years at a speed of 0.75c. Unfortunately, at this point in his journey, the structure of his ship undergoes mechanical breakdown and the ship explodes. How old is Rick when his brother dies?arrow_forwardHi, I have canceled, why did you charge me again?arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College





