Chapter 21, Problem 16A

Figure 21−9 shows a compound gear train. Gears B and C are keyed to the same shaft; therefore, they turn at the same speed. Gear A and gear C are driving gears. Gear B and gear D are driven gears. Set up a proportion for each problem and determine the unknown values, x, y, and z in the table. Round the answers to 1 decimal place where necessary.

To determine

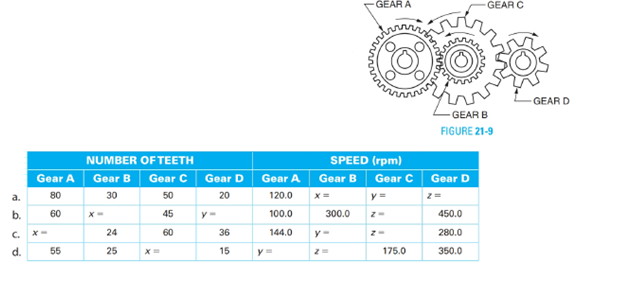
(a)

To find the speed of the different gears given in the problem.

Answer to Problem 16A

Speed of gear B is $x=$ $320$ rpm.

Speed of gear C is $y=$ $320$ rpm.

Speed of gear D is $z=$ $800$ rpm.

Explanation of Solution

Given information:

A gear and pinion arrangement is given as below.

  

$\begin{array}{l}\text{Number of teeth on gear A}=80,\\ \text{Number of teeth on gear B}=30\text{,}\\ \text{Number of teeth on gear C}=50,\\ \text{Number of teeth on gear D}=20\text{,}\end{array}$ Y1 $\begin{array}{l}\text{speed of gear A}=120.0\text{ rpm, }\\ \text{speed of gear B}=x\text{rpm,}\\ \text{speed of gear C}=y\text{rpm,}\\ \text{speed of gear D}=z\text{rpm,}\end{array}$

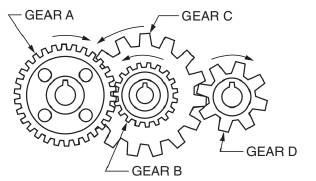
Calculation:

We have been given below information,

  $\begin{array}{l}\text{Number of teeth on gear A}=80,\\ \text{Number of teeth on gear B}=30\text{,}\\ \text{Number of teeth on gear C}=50,\\ \text{Number of teeth on gear D}=20\text{,}\end{array}$ y $\begin{array}{l}\text{speed of gear A}=120.0\text{ rpm, }\\ \text{speed of gear B}=x\text{rpm,}\\ \text{speed of gear C}=y\text{rpm,}\\ \text{speed of gear D}=z\text{rpm,}\end{array}$

As we know that in a gear arrangement,

13 $\frac{\text{Teeth in driving gear }}{\text{Teeth in driven gear }}=\frac{\text{Revolutions in driven gear }}{\text{Revolution in driving gear}}$

So,

  $\begin{array}{l}\frac{\text{Teeth in driving gear A }}{\text{Teeth in driven gear B}}=\frac{\text{Revolutions in driven gear B }}{\text{Revolution in driving gear}\text{A}}\\ \Rightarrow \frac{80}{30}=\frac{x\text{ rpm}}{120.0}\\ \text{Applying cross multiplication,}\\ \Rightarrow 30x=80\times 120.0\text{ rpm}\\ \Rightarrow x=\frac{80\times 120.0}{30}\text{}\text{rpm}\\ \Rightarrow x=320\text{ rpm}\end{array}$

Hence, speed of gear B is

  $320$ rpm.

Since, gear B and C are on same shaft. So, speed of both gear is equal.

Therefore, speed of gear C is $y=$ $320$ rpm.

Again,

  $\begin{array}{l}\frac{\text{Teeth in driving gear C }}{\text{Teeth in driven gear D}}=\frac{\text{Revolutions in driven gear D }}{\text{Revolution in driving gear}C}\\ \Rightarrow \frac{50}{20}=\frac{z\text{ rpm}}{320.0}\\ \text{Applying cross multiplication,}\\ \Rightarrow 20z=50\times 320.0\text{ rpm}\\ \Rightarrow z=\frac{50\times 320.0}{20}\text{}\text{rpm}\\ \Rightarrow z=800.0\text{ rpm}\end{array}$

Hence, speed of gear D is $800$ rpm.

Thus, speed of gear B is $x=$ $320$ rpm.

Speed of gear C is $y=$ $320$ rpm.

Speed of gear D is $z=$ $800$ rpm.

To determine

(b)

To find the number of teeth in the gear and the speed of the gear.

Answer to Problem 16A

Number of teeth in gear B is $x=$ 20.

Number of teeth in gear D is $y=$ $30$.

Speed of gear C is $z=$ $300.0$ rpm.

Explanation of Solution

Given information:

A gear and pinion arrangement is given as below.

  

$\begin{array}{l}\text{Number of teeth on gear A}=60,\\ \text{Number of teeth on gear B}=x\text{,}\\ \text{Number of teeth on gear C}=45,\\ \text{Number of teeth on gear D}=y\text{,}\end{array}$ $\begin{array}{l}\text{speed of gear A}=100.0\text{ rpm, }\\ \text{speed of gear B}=300.0\text{rpm,}\\ \text{speed of gear C}=z\text{rpm,}\\ \text{speed of gear D}=450.0\text{rpm,}\end{array}$

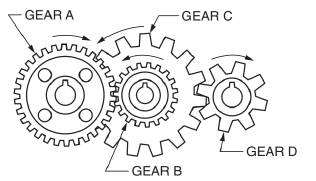
Calculation:

We have been given below information,

  $\begin{array}{l}\text{Number of teeth on gear A}=60,\\ \text{Number of teeth on gear B}=x\text{,}\\ \text{Number of teeth on gear C}=45,\\ \text{Number of teeth on gear D}=y\text{,}\end{array}$ $\begin{array}{l}\text{speed of gear A}=100.0\text{ rpm, }\\ \text{speed of gear B}=300.0\text{rpm,}\\ \text{speed of gear C}=z\text{rpm,}\\ \text{speed of gear D}=450.0\text{rpm,}\end{array}$

As we know that in a gear arrangement,

  $\frac{\text{Teeth in driving gear }}{\text{Teeth in driven gear }}=\frac{\text{Revolutions in driven gear }}{\text{Revolution in driving gear}}$

So,

  $\begin{array}{l}\frac{\text{Teeth in driving gear A }}{\text{Teeth in driven gear B}}=\frac{\text{Revolutions in driven gear B }}{\text{Revolution in driving gear}\text{A}}\\ \Rightarrow \frac{60}{x}=\frac{\text{300}\text{.0 }}{100.0}\\ \text{Applying cross multiplication,}\\ \Rightarrow 300.0x=60\times 100.0\\ \Rightarrow x=\frac{60\times 100.0}{300.0}\text{}\\ \Rightarrow x=20\end{array}$

Hence, number of teeth in gear B is $x=$ 20.

Since, gear B and C are on same shaft. So, speed of both gear is equal.

Therefore, speed of gear C is $z=$ $300.0$ rpm.

Again,

  $\begin{array}{l}\frac{\text{Teeth in driving gear C }}{\text{Teeth in driven gear D}}=\frac{\text{Revolutions in driven gear D }}{\text{Revolution in driving gear}C}\\ \Rightarrow \frac{45}{y}=\frac{\text{450}\text{.0}}{300.0}\\ \text{Applying cross multiplication,}\\ \Rightarrow 450.0y=45\times 300.0\\ \Rightarrow y=\frac{45\times 300.0}{450.0}\text{}\\ \Rightarrow y=30\end{array}$

Hence, number of teeth in gear D is $y=$ $30$.

Thus, number of teeth in gear B is $x=$ 20.

Number of teeth in gear D is $y=$ $30$.

Speed of gear C is $z=$ $300.0$ rpm.

To determine

(c)

To find the number of teeth as well as speed of the gear.

Answer to Problem 16A

Number of teeth in gear A is $x=$ $20.57$.

Speed of gear B is $y=$ $168.0$ rpm.

Speed of gear C is $z=$ $168.0$ rpm.

Explanation of Solution

Given information:

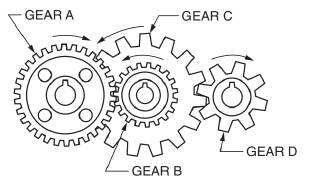
A gear and pinion arrangement is given as below.

  

$\begin{array}{l}\text{Number of teeth on gear A}=x,\\ \text{Number of teeth on gear B}=24\text{,}\\ \text{Number of teeth on gear C}=60,\\ \text{Number of teeth on gear D}=36\text{,}\end{array}$ $\begin{array}{l}\text{speed of gear A}=144.0\text{ rpm, }\\ \text{speed of gear B}=y\text{rpm,}\\ \text{speed of gear C}=z\text{rpm,}\\ \text{speed of gear D}=280.0\text{rpm,}\end{array}$

Calculation:

We have been given below information,

  $\begin{array}{l}\text{Number of teeth on gear A}=x,\\ \text{Number of teeth on gear B}=24\text{,}\\ \text{Number of teeth on gear C}=60,\\ \text{Number of teeth on gear D}=36\text{,}\end{array}$ $\begin{array}{l}\text{speed of gear A}=144.0\text{ rpm, }\\ \text{speed of gear B}=y\text{rpm,}\\ \text{speed of gear C}=z\text{rpm,}\\ \text{speed of gear D}=280.0\text{rpm,}\end{array}$

As we know that in a gear arrangement,

  $\frac{\text{Teeth in driving gear }}{\text{Teeth in driven gear }}=\frac{\text{Revolutions in driven gear }}{\text{Revolution in driving gear}}$

So,

  $\begin{array}{l}\frac{\text{Teeth in driving gear A }}{\text{Teeth in driven gear B}}=\frac{\text{Revolutions in driven gear B }}{\text{Revolution in driving gear}\text{A}}\\ \Rightarrow \frac{x}{24}=\frac{\text{144}\text{.0 }}{y}\\ \text{Applying cross multiplication,}\\ \Rightarrow xy=24\times 144.0\mathrm{...}\text{eq(i)}\end{array}$

Since, gear B and C are on same shaft. So, speed of both gear is equal. i.e. $y=z$.

Again,

  $\begin{array}{l}\frac{\text{Teeth in driving gear C }}{\text{Teeth in driven gear D}}=\frac{\text{Revolutions in driven gear D }}{\text{Revolution in driving gear}C}\\ \Rightarrow \frac{60}{36}=\frac{280.0}{z}\\ \text{Applying cross multiplication,}\\ \Rightarrow 60z=36\times 280.0\\ \Rightarrow z=\frac{36\times 280.0}{60}\text{}\\ \Rightarrow z=168\end{array}$

Hence, speed of gear B and gear C is $168$ rpm. i.e. $y=168$ and $z=168$.

Putting, $y=168$ in eq(i),

  $\begin{array}{l}xy=24\times 144.0\\ \Rightarrow 168x=24\times 144.0\text{ {Put }y=168\text{}}\\ \Rightarrow x=\frac{24\times 144.0}{168}\\ \Rightarrow x=20.57\end{array}$

Thus, number of teeth in gear A is $x=$ $20.57$.

Speed of gear B is $y=$ $168.0$ rpm.

Speed of gear C is $z=$ $168.0$ rpm.

To determine

(d)

To find the speed of the different gears and the number of teeth.

Answer to Problem 16A

Number of teeth in gear C is $x=$ 30.

Speed of gear A is $y=79.55$ rpm.

Speed of gear B is $z=175.0$ rpm.

Explanation of Solution

Given information:

A gear and pinion arrangement is given as below.

  

$\begin{array}{l}\text{Number of teeth on gear A}=55,\\ \text{Number of teeth on gear B}=25\text{,}\\ \text{Number of teeth on gear C}=x,\\ \text{Number of teeth on gear D}=15\text{,}\end{array}$ $\begin{array}{l}\text{speed of gear A}=y\text{ rpm, }\\ \text{speed of gear B}=z\text{rpm,}\\ \text{speed of gear C}=175.0\text{rpm,}\\ \text{speed of gear D}=350.0\text{rpm,}\end{array}$

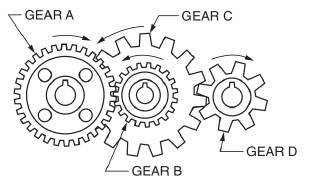
Calculation:

We have been given below information,

  $\begin{array}{l}\text{Number of teeth on gear A}=55,\\ \text{Number of teeth on gear B}=25\text{,}\\ \text{Number of teeth on gear C}=x,\\ \text{Number of teeth on gear D}=15\text{,}\end{array}$ $\begin{array}{l}\text{speed of gear A}=y\text{ rpm, }\\ \text{speed of gear B}=z\text{rpm,}\\ \text{speed of gear C}=175.0\text{rpm,}\\ \text{speed of gear D}=350.0\text{rpm,}\end{array}$

As we know that in a gear arrangement,

  $\frac{\text{Teeth in driving gear }}{\text{Teeth in driven gear }}=\frac{\text{Revolutions in driven gear }}{\text{Revolution in driving gear}}$

So,

  $\begin{array}{l}\frac{\text{Teeth in driving gear A }}{\text{Teeth in driven gear B}}=\frac{\text{Revolutions in driven gear B }}{\text{Revolution in driving gear}\text{A}}\\ \Rightarrow \frac{55}{25}=\frac{z}{y}\\ \text{Applying cross multiplication,}\\ \Rightarrow 55y=25z\mathrm{...}\text{eq(i)}\end{array}$

Since, gear B and C are on same shaft. So, speed of both gear is equal. i.e. $z=175.0$.

Putting $x=175.0$ in above eq(i),

  $\begin{array}{l}55y=25\times 175.0\\ \Rightarrow y=\frac{25\times 175.0}{55}\\ \Rightarrow y=79.55\end{array}$

Hence, speed of gear A is $y=79.55$ rpm.

Again,

  $\begin{array}{l}\frac{\text{Teeth in driving gear C }}{\text{Teeth in driven gear D}}=\frac{\text{Revolutions in driven gear D }}{\text{Revolution in driving gear}C}\\ \Rightarrow \frac{x}{15}=\frac{350.0}{175.0}\\ \text{Applying cross multiplication,}\\ \Rightarrow 175.0x=15\times 350.0\\ \Rightarrow x=\frac{15\times 350.0}{175.0}\text{}\\ \Rightarrow x=30\end{array}$

Hence, number of teeth in gear C is $x=$ 30.

Thus, number of teeth in gear C is $x=$ 30.

Speed of gear A is $y=79.55$ rpm.

Speed of gear B is $z=175.0$ rpm.