Chapter 2.1, Problem 112E

To determine

To determine:

a) We can see from the table that with the increase in value of $x$ , there is decrease in value of $y$ , hence we can say that coefficient of correlation is negative

b) Equation of least squares is $y=-2.9866x+24.92$ and correlation coefficient $r=-0.9995$

Plot is

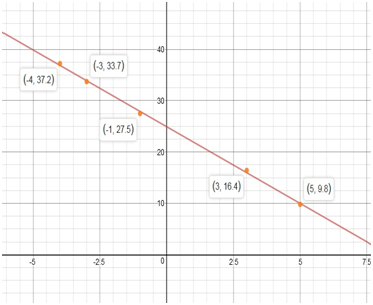
c) Predicted value of y at $x=2.4$ is $17.752$

Given information: Five points

$x$	−4	−3	−1	3	5
$y$	3.7	33.7	27.5	16.4	9.8

Formula used: Slope, $m=\frac{\sum _{i=1}^n(x_i-\overline{X})(y_i-\overline{Y})}{\sum _{i=1}^n{(x_i-\overline{X})}^2}$

Y axis intercept, $b=\overline{Y}-m\overline{X}$

Correlation Coefficient,$r=\frac{\sum _{i=1}^n(x_i-\overline{X})(y_i-\overline{Y})}{\sqrt{\sum _{i=1}^n{(x_i-\overline{X})}^2}\sqrt{\sum _{i=1}^n{(y_i-\overline{Y})}^2}}$

Where $x_i$ and $y_i$ are the $i$ th entry of $x$ and $y$ ; $\overline{X}$ and $\overline{Y}$ are means of $x$ and $y$

Calculation:

Step 1: Calculate the mean of $x$ and $y$

$\begin{array}{â}\overline{X}=\frac{(-4)+(-3)+(-1)+3+5}{5}=0\\ \overline{Y}=\frac{37.2+33.7+27.5+16.4+9.8}{5}=24.92\end{array}$

Step 2: Plot the table as shown

$i$	$x_i$	$y_i$	$x_i-\overline{X}$	$y_i-\overline{Y}$	${(x_i-\overline{X})}^2$	$(x_i-\overline{X})(y_i-\overline{Y})$	${(y_i-\overline{Y})}^2$
1	-4	37.2	-4	12.28	16	-49.12	150.7984
2	-3	33.7	-3	8.78	9	-26.34	77.0884
3	-1	27.5	-1	2.58	1	-2.58	6.6564
4	3	16.4	3	-8.52	9	-25.56	72.5904
5	5	9.8	5	-15.12	25	-75.6	228.6144
					${\displaystyle \sum _{i=1}^n{(x_i-\overline{X})}^2}=60$	${\displaystyle \sum _{i=1}^n(x_i-\overline{X})(y_i-\overline{Y})}=-179.2$	${\displaystyle \sum _{i=1}^n{(y_i-\overline{Y})}^2}=535.7480$

Step 3: Calculate the slope $m=\frac{\sum _{i=1}^n(x_i-\overline{X})(y_i-\overline{Y})}{\sum _{i=1}^n{(x_i-\overline{X})}^2}=\frac{-179.2}{60}\approx -2.9866$

Step 4: Calculate $y$ intercept $b=\overline{Y}-m\overline{X}=24.92-(-2.9866\times 0)\approx 24.92$

The slope of the line is $-2.9866$ and y intercept is $24.92$

Using slope intercept form, $y=mx+b$ ,equation is $y=-2.9866x+24.92$;

Step 5: Draw the scatter plot

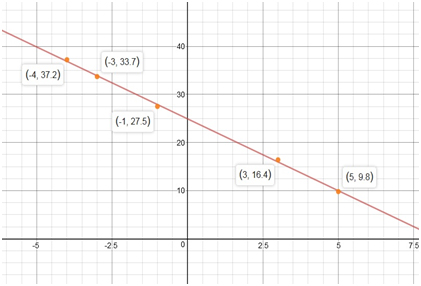
Step 6: Calculate the Correlation coefficient

$r=\frac{\sum _{i=1}^n(x_i-\overline{X})(y_i-\overline{Y})}{\sqrt{\sum _{i=1}^n{(x_i-\overline{X})}^2}\sqrt{\sum _{i=1}^n{(y_i-\overline{Y})}^2}}=\frac{-179.2}{\sqrt{60}\times \sqrt{535.7480}}\approx -0.9995$

Step 7: Prediction for $x=2.4$ ; plug $x=2.4$ in $y=-2.9866x+24.92$

$y=-2.9866\left(2.4\right)+24.92=17.752$