Chapter 20, Problem 3P

(a)

To determine

The current in the metal rod.

Answer to Problem 3P

The current in the metal rod is $\underset{\_}{3.3\times {10}^{-5}\text{A}}$.

Explanation of Solution

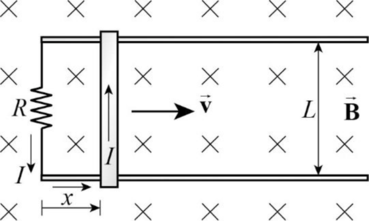
Figure $1$

Write the expression for the induced emf in the metal rod.

$\epsilon =vBL$        (I)

Here, $\epsilon$ is the induced emf, $L$ is the length of the rod, $v$ is the velocity.

Write the expression for the current in the metal rod.

$I=\frac{\epsilon }{R}$        (II)

Here, $I$ is the current, $R$ is the resistance.

Use equation (II) in (I) to solve for $I$.

$I=\frac{vBL}{R}$        (III)

Conclusion:

Substitute $16\text{cm}/\text{s}$ for $v$, $0.75\text{T}$ for $B$, $5.0\text{cm}$ for $L$, $180\Omega$ for $R$ in equation (III) to find $I$.

    $\begin{array}{c}I=\frac{\left(16\text{cm}\times \frac{{10}^{-2}\text{m}}{1\text{cm}}/\text{s}\right)\left(0.75\text{T}\right)\left(5.0\text{cm}\times \frac{{10}^{-2}\text{m}}{1\text{cm}}\right)}{\left(180\Omega \right)}\\ =\frac{0.0060\text{V}}{180\Omega }\\ =3.3\times {10}^{-5}\text{A}\end{array}$

Therefore, the current in the metal rod is $\underset{\_}{3.3\times {10}^{-5}\text{A}}$.

(b)

To determine

The energy dissipated in the resistor.

Answer to Problem 3P

The rate of energy dissipated in the resistor is $\underset{\_}{2.0\times {10}^{-7}\text{W}}$.

Explanation of Solution

Write the expression for the energy dissipated in the resistor.

$P=I^{2}R$        (IV)

Here, $P$ is the power or the rate of energy dissipated in the resistor.

Conclusion:

Substitute $3.3\times {10}^{-5}\text{A}$ for $I$, $180\Omega$ for $R$ in equation (IV) to find $P$.

    $\begin{array}{c}P={\left(3.3\times {10}^{-5}\text{A}\right)}^2\left(180\Omega \right)\\ =2.0\times {10}^{-7}\text{W}\end{array}$

Therefore, the energy dissipated in the resistor is $\underset{\_}{2.0\times {10}^{-7}\text{W}}$.

(c)

To determine

The magnetic force on the metal rod.

Answer to Problem 3P

The magnetic force on the metal rod is $\underset{\_}{1.3\times {10}^{-6}\text{N in the left direction}}$.

Explanation of Solution

Write the expression for the magnetic force.

    $\overrightarrow{F}=I\overrightarrow{L}\times \overrightarrow{B}$        (V)

Here, $F$ is the magnetic force.

Conclusion:

Substitute $3.3\times {10}^{-5}\text{A}$ for $I$, $5.0\text{cm}\widehat{j}$ for $\overrightarrow{L}$, $0.75\text{T}\left(-\widehat{k}\right)$ for $\overrightarrow{B}$ in equation (V) to find $\overrightarrow{F}$.

    $\begin{array}{c}\overrightarrow{F}=\left(3.3\times {10}^{-5}\text{A}\right)\left(5.0\text{cm}\widehat{j}\right)\times \left(0.75\text{T}\left(-\widehat{k}\right)\right)\\ =\left(3.3\times {10}^{-5}\text{A}\right)\left(5.0\text{cm}\right)\left(0.75\text{T}\right)\left(\widehat{j}\times -\widehat{k}\right)\\ =1.3\times {10}^6\text{N}\left(-\widehat{i}\right)\end{array}$

Therefore, the magnetic force on the metal rod is $\underset{\_}{1.3\times {10}^{-6}\text{N in the left direction}}$.