Chapter 20, Problem 19A

To determine

(a)

The indicated ratios in lowest fractional form.

Answer to Problem 19A

The ratio of dimension A to dimension B is $\frac{2}{1}$.

Explanation of Solution

Given:

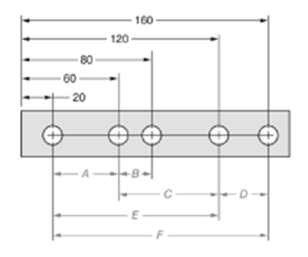
The given figure is as follows:

  

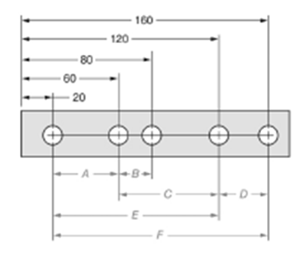
Concept used:

The dimension can be calculated by subtracting the distance of near hole from the one which is farther.

Calculation:

From the given figure, it is clear that the measure of dimension A is given by,

  $\begin{array}{l}A=60-20\\ A=40\end{array}$

The measure of dimension B is given by,

  $\begin{array}{l}B=80-60\\ B=20\end{array}$

The ratio of dimension A to dimension B is given by,

  $\begin{array}{c}\frac{A}{B}=\frac{40}{20}\\ \frac{A}{B}=\frac{2}{1}\end{array}$

Thus, the ratio is $\frac{2}{1}$.

Conclusion:

The ratio of Dimension A to Dimension B is $\frac{2}{1}$.

To determine

(b)

The indicated ratios in lowest fractional form.

Answer to Problem 19A

The ratio of dimension A to dimension C is $\frac{2}{1}$.

Explanation of Solution

Given:

The given figure is as follows:

  

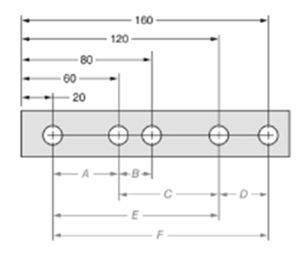
Concept used:

The dimension can be calculated by subtracting the distance of near hole from the one which is farther.

Calculation:

From the given figure, it is clear that the measure of dimension A is given by,

  $\begin{array}{l}A=60-20\\ A=40\end{array}$

The measure of dimension C is given by,

  $\begin{array}{l}C=120-60\\ C=60\end{array}$

The ratio of dimension A to dimension C is given by,

  $\begin{array}{c}\frac{A}{C}=\frac{40}{60}\\ \frac{A}{C}=\frac{2}{3}\end{array}$

Thus, the ratio is $\frac{2}{3}$.

Conclusion:

The ratio of Dimension A to Dimension C is $\frac{2}{3}$.

To determine

(c)

The indicated ratios in lowest fractional form.

Answer to Problem 19A

The ratio of dimension C to dimension D is $\frac{3}{2}$.

Explanation of Solution

Given:

The given figure is as follows:

  

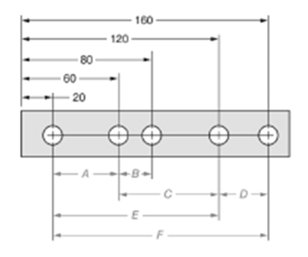
Concept used:

The dimension can be calculated by subtracting the distance of near hole from the one which is farther.

Calculation:

From the given figure, it is clear that the measure of dimension C is given by,

  $\begin{array}{l}C=120-60\\ C=60\end{array}$

The measure of dimension D is given by,

  $\begin{array}{l}D=160-120\\ D=40\end{array}$

The ratio of dimension C to dimension D is given by,

  $\begin{array}{c}\frac{C}{D}=\frac{60}{40}\\ \frac{C}{D}=\frac{3}{2}\end{array}$

Thus, the ratio is $\frac{3}{2}$.

Conclusion:

The ratio of Dimension C to Dimension D is $\frac{3}{2}$.

To determine

(d)

The indicated ratios in lowest fractional form.

Answer to Problem 19A

The ratio of dimension C to dimension E is $\frac{3}{5}$.

Explanation of Solution

Given:

The given figure is as follows:

  

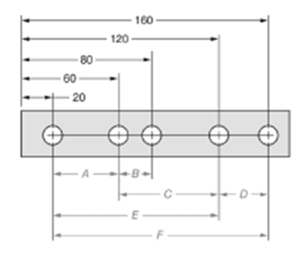
Concept used:

The dimension can be calculated by subtracting the distance of near hole from the one which is farther.

Calculation:

From the given figure, it is clear that the measure of dimension C is given by,

  $\begin{array}{l}C=120-60\\ C=60\end{array}$

The measure of dimension E is given by,

  $\begin{array}{l}E=120-20\\ E=100\end{array}$

The ratio of dimension C to dimension E is given by,

  $\begin{array}{c}\frac{C}{E}=\frac{60}{100}\\ \frac{C}{E}=\frac{3}{5}\end{array}$

Thus, the ratio is $\frac{3}{5}$.

Conclusion:

The ratio of Dimension C to Dimension E is $\frac{3}{5}$.

To determine

(e)

The indicated ratios in lowest fractional form.

Answer to Problem 19A

The ratio of dimension D to dimension F is $\frac{2}{7}$.

Explanation of Solution

Given:

The given figure is as follows:

  

Concept used:

The dimension can be calculated by subtracting the distance of near hole from the one which is farther.

Calculation:

From the given figure, it is clear that the measure of dimension D is given by,

  $\begin{array}{l}D=160-120\\ D=40\end{array}$

The measure of dimension F is given by,

  $\begin{array}{l}F=160-20\\ F=140\end{array}$

The ratio of dimension D to dimension F is given by,

  $\begin{array}{c}\frac{D}{F}=\frac{40}{140}\\ \frac{D}{F}=\frac{2}{7}\end{array}$

Thus, the ratio is $\frac{2}{7}$.

Conclusion:

The ratio of Dimension D to Dimension F is $\frac{2}{7}$.

To determine

(f)

The indicated ratios in lowest fractional form.

Answer to Problem 19A

The ratio of dimension F to dimension B is $\frac{7}{1}$.

Explanation of Solution

Given:

The given figure is as follows:

  

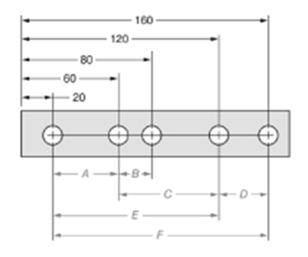
Concept used:

The dimension can be calculated by subtracting the distance of near hole from the one which is farther.

Calculation:

From the given figure, it is clear that the measure of dimension F is given by,

  $\begin{array}{l}F=160-20\\ F=140\end{array}$

The measure of dimension B is given by,

  $\begin{array}{l}B=80-60\\ B=20\end{array}$

The ratio of dimension F to dimension B is given by,

  $\begin{array}{c}\frac{F}{B}=\frac{140}{20}\\ \frac{F}{B}=\frac{7}{1}\end{array}$

Thus, the ratio is $\frac{7}{1}$.

Conclusion:

The ratio of Dimension F to Dimension B is $\frac{7}{1}$.

To determine

(g)

The indicated ratios in lowest fractional form.

Answer to Problem 19A

The ratio of dimension F to dimension C is $\frac{7}{3}$.

Explanation of Solution

Given:

The given figure is as follows:

  

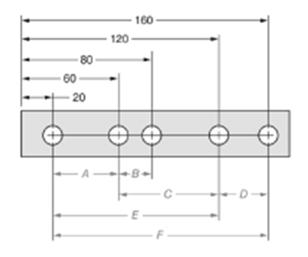
Concept used:

The dimension can be calculated by subtracting the distance of near hole from the one which is farther.

Calculation:

From the given figure, it is clear that the measure of dimension F is given by,

  $\begin{array}{l}F=160-20\\ F=140\end{array}$

The measure of dimension C is given by,

  $\begin{array}{l}C=120-60\\ C=60\end{array}$

The ratio of dimension F to dimension C is given by,

  $\begin{array}{c}\frac{F}{C}=\frac{140}{60}\\ \frac{F}{C}=\frac{7}{3}\end{array}$

Thus, the ratio is $\frac{7}{3}$.

Conclusion:

The ratio of Dimension F to Dimension C is $\frac{7}{3}$.

To determine

(h)

The indicated ratios in lowest fractional form.

Answer to Problem 19A

The ratio of dimension E to dimension A is $\frac{5}{2}$.

Explanation of Solution

Given:

The given figure is as follows:

  

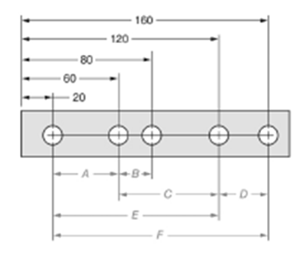
Concept used:

The dimension can be calculated by subtracting the distance of nearer hole from the one which is farther.

Calculation:

From the given figure, it is clear that the measure of dimension E is given by,

  $\begin{array}{l}E=120-20\\ E=100\end{array}$

The measure of dimension A is given by,

  $\begin{array}{l}A=60-20\\ A=40\end{array}$

The ratio of dimension E to dimension A is given by,

  $\begin{array}{c}\frac{E}{A}=\frac{100}{40}\\ \frac{E}{A}=\frac{5}{2}\end{array}$

Thus, the ratio is $\frac{5}{2}$.

Conclusion:

The ratio of Dimension E to Dimension A is $\frac{5}{2}$.

To determine

(i)

The indicated ratios in lowest fractional form.

Answer to Problem 19A

The ratio of dimension D to dimension B is $\frac{2}{1}$.

Explanation of Solution

Given:

The given figure is as follows:

  

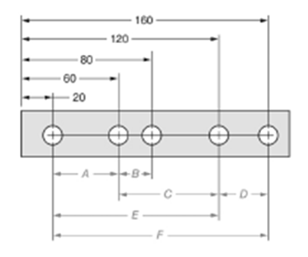
Concept used:

The dimension can be calculated by subtracting the distance the near hole from the one which is farther.

Calculation:

From the given figure, it is clear that the measure of dimension D is given by,

  $\begin{array}{l}D=160-120\\ D=40\end{array}$

The measure of dimension B is given by,

  $\begin{array}{l}B=80-60\\ B=20\end{array}$

The ratio of dimension D to dimension B is given by,

  $\begin{array}{c}\frac{D}{B}=\frac{40}{20}\\ \frac{D}{B}=\frac{2}{1}\end{array}$

Thus, the ratio is $\frac{2}{1}$.

Conclusion:

The ratio of Dimension D to Dimension B is $\frac{2}{1}$.

To determine

(j)

The indicated ratios in lowest fractional form.

Answer to Problem 19A

The ratio of dimension C to dimension F is $\frac{3}{7}$.

Explanation of Solution

Given:

The given figure is as follows:

  

Concept used:

The dimension can be calculated by subtracting the distance of nearer hole from the one which is farther.

Calculation:

From the given figure, it is clear that the measure of dimension C is given by,

  $\begin{array}{l}C=120-60\\ C=60\end{array}$

The measure of dimension F is given by,

  $\begin{array}{l}F=160-20\\ F=140\end{array}$

The ratio of dimension C to dimension F is given by,

  $\begin{array}{c}\frac{C}{F}=\frac{60}{140}\\ \frac{C}{F}=\frac{3}{7}\end{array}$

Thus, the ratio is $\frac{3}{7}$.

Conclusion:

The ratio of Dimension C to Dimension F is $\frac{3}{7}$.