Precalculus - A Custom Text for UNLV
6th Edition
ISBN: 9781133150572
Author: Redlin Watson Stewart
Publisher: Compliation @ Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 2, Problem 1T
(a)
To determine
To describe: Whether the graph is function and if it is a function then whether it is one-to-one.
(a)
Expert Solution
Explanation of Solution
The given graph is,
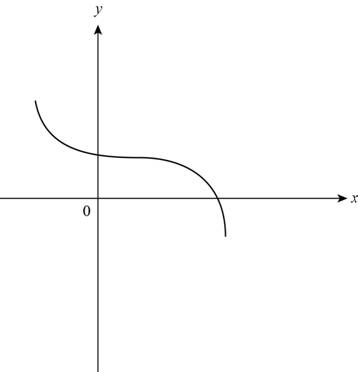
Figure (1)
Use vertical line test to find whether the given graph in Figure (1) is function or not.
Vertical line test states that, if a vertical line intersects the graph at more than one point than the graph is not a function.
Use horizontal line test to find whether the function is one-to-one.
Horizontal line states that if a horizontal line intersects the function more than once than the function is not one-to-one.
Draw a vertical line and horizontal line as shown below,
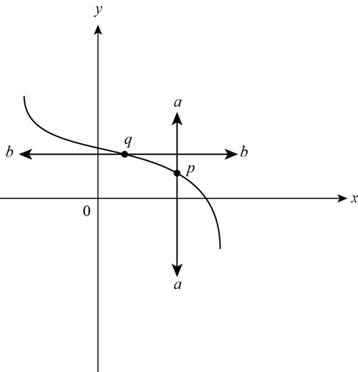
Figure (2)
From Figure (2) observe that line a intersect the graph at only one point p and line b intersect the graph of function at one point q.
The vertical line intersects at one point and horizontal line also intersects at one point.
Thus, the given graph is a function and it is one-to-one.
(b)
To determine
To describe: Whether the graph is function and if it is a function then whether it is one-to-one.
(b)
Expert Solution
Explanation of Solution
The given graph is,
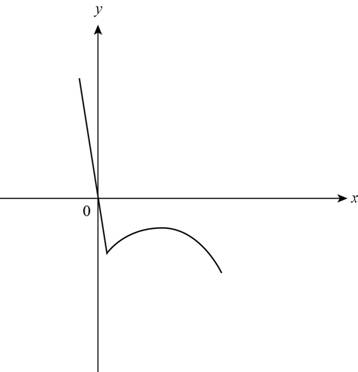
Figure (3)
Use vertical line test to find whether the given graph in Figure (1) is function or not.
Vertical line test states that, if a vertical line intersects the graph at more than one point than the graph is not a function.
Use horizontal line test to find whether the function is one-to-one.
Horizontal line states that if a horizontal line intersects the function more than once than the function is not one-to-one.
Draw a vertical line and a horizontal line as shown below,
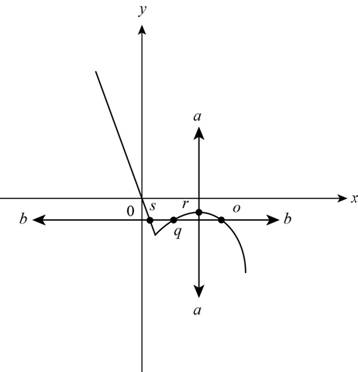
Figure (4)
From Figure (4) it can be observe that line a intersect at only one point r and line b intersect the function at three points s, q and p.
Vertical line intersects at only one point. So the graph is a function.
Horizontal line intersects at more than one point. So, the function is not one-to-one.
Thus, the given graph is a function but not one-to-one.
(c)
To determine
To describe: Whether the graph is function and if it is a function then whether it is one-to-one.
(c)
Expert Solution
Explanation of Solution
The given graph is,
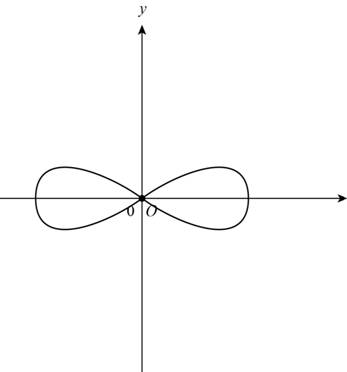
Figure (5)
Use vertical line test to find whether the given graph in Figure (5) is function or not.
Vertical line test states that, if a vertical line intersects the graph at more than one point than the graph is not a function.
Use horizontal line test to find whether the function is one-to-one.
Horizontal line states that if a horizontal line intersects the function more than once than the function is not one-to-one.
Draw a vertical line and a horizontal line as shown below,
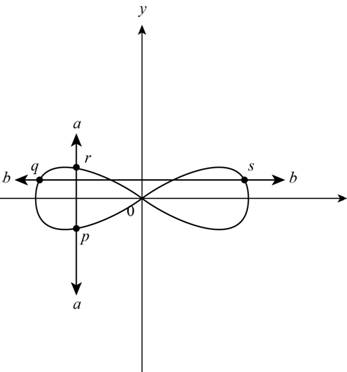
Figure (6)
From Figure (2) it can be observe that vertical line a intersect at points p and r. The horizontal line b intersect the function at points q and s.
So, vertical line intersects at more than one point and horizontal line also intersects at more than one point.
Thus, the given graph is not a function and not one-to-one.
(d)
To determine
To describe: Whether the graph is function and if it is a function then whether it is one-to-one.
(d)
Expert Solution
Explanation of Solution
The given graph is,
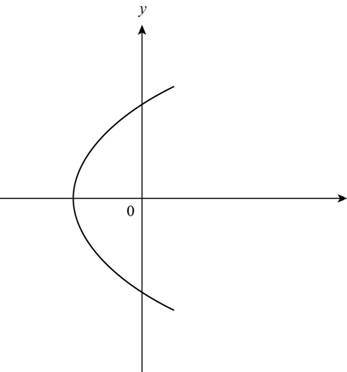
Figure (7)
Use vertical line test to find whether the given graph in Figure (7) is function or not.
Vertical line test states that, if a vertical line intersects the graph at more than one point than the graph is not a function.
Use horizontal line test to find whether the function is one-to-one.
Horizontal line states that if a horizontal line intersects the function more than once than the function is not one-to-one.
Draw a vertical line and horizontal line as shown below,
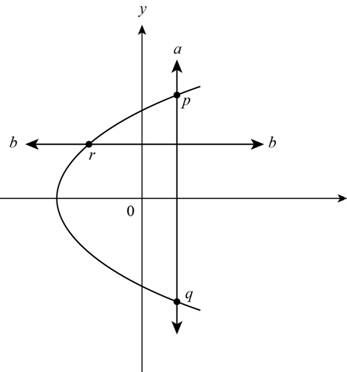
Figure (8)
From Figure (8) it can be observe that vertical line a intersects at two points p and q. The horizontal line b intersects the function at only one point r.
Vertical line intersects the graph at more than one point and horizontal line intersects at only one point.
Thus, the given graph is a not a function but one-to-one.
Chapter 2 Solutions
Precalculus - A Custom Text for UNLV
Ch. 2.1 - Prob. 1ECh. 2.1 - For a function f, the set of all possible inputs...Ch. 2.1 - (a) Which of the following functions have 5 in...Ch. 2.1 - A function is given algebraically by the formula...Ch. 2.1 - Prob. 5ECh. 2.1 - Prob. 6ECh. 2.1 - Prob. 7ECh. 2.1 - Prob. 8ECh. 2.1 - Prob. 9ECh. 2.1 - Prob. 10E
Ch. 2.1 - Prob. 11ECh. 2.1 - Prob. 12ECh. 2.1 - Prob. 13ECh. 2.1 - Prob. 14ECh. 2.1 - Prob. 15ECh. 2.1 - Prob. 16ECh. 2.1 - Prob. 17ECh. 2.1 - Prob. 18ECh. 2.1 - Prob. 19ECh. 2.1 - Prob. 20ECh. 2.1 - Prob. 21ECh. 2.1 - Prob. 22ECh. 2.1 - Prob. 23ECh. 2.1 - Prob. 24ECh. 2.1 - Prob. 25ECh. 2.1 - Prob. 26ECh. 2.1 - Prob. 27ECh. 2.1 - Prob. 28ECh. 2.1 - Prob. 29ECh. 2.1 - Prob. 30ECh. 2.1 - Prob. 31ECh. 2.1 - Prob. 32ECh. 2.1 - Prob. 33ECh. 2.1 - Prob. 34ECh. 2.1 - Prob. 35ECh. 2.1 - Prob. 36ECh. 2.1 - Prob. 37ECh. 2.1 - Prob. 38ECh. 2.1 - Prob. 39ECh. 2.1 - Prob. 40ECh. 2.1 - Prob. 41ECh. 2.1 - Prob. 42ECh. 2.1 - Prob. 43ECh. 2.1 - Prob. 44ECh. 2.1 - Prob. 45ECh. 2.1 - Prob. 46ECh. 2.1 - Prob. 47ECh. 2.1 - Prob. 48ECh. 2.1 - Prob. 49ECh. 2.1 - Prob. 50ECh. 2.1 - Prob. 51ECh. 2.1 - Prob. 52ECh. 2.1 - Prob. 53ECh. 2.1 - Prob. 54ECh. 2.1 - Prob. 55ECh. 2.1 - Prob. 56ECh. 2.1 - Prob. 57ECh. 2.1 - Prob. 58ECh. 2.1 - Prob. 59ECh. 2.1 - Prob. 60ECh. 2.1 - Prob. 61ECh. 2.1 - Prob. 62ECh. 2.1 - Prob. 63ECh. 2.1 - Prob. 64ECh. 2.1 - Prob. 65ECh. 2.1 - Prob. 66ECh. 2.1 - Prob. 67ECh. 2.1 - Prob. 68ECh. 2.1 - Prob. 69ECh. 2.1 - Prob. 70ECh. 2.1 - Prob. 71ECh. 2.1 - Prob. 72ECh. 2.1 - Prob. 73ECh. 2.1 - Prob. 74ECh. 2.1 - Relativity According to the Theory of Relativity,...Ch. 2.1 - Income Tax In a certain country, income tax T is...Ch. 2.1 - Internet Purchases An Internet bookstore charges...Ch. 2.1 - Cost of a Hotel Stay A hotel chain charges 75 each...Ch. 2.1 - Speeding Tickets In a certain state the maximum...Ch. 2.1 - Height of Grass A home owner mows the lawn every...Ch. 2.1 - Prob. 81ECh. 2.1 - Prob. 82ECh. 2.1 - Prob. 83ECh. 2.1 - Prob. 84ECh. 2.1 - Prob. 85ECh. 2.2 - Prob. 1ECh. 2.2 - Prob. 2ECh. 2.2 - Prob. 3ECh. 2.2 - Match the function with its graph. (a) f(x) = x2...Ch. 2.2 - Prob. 5ECh. 2.2 - Prob. 6ECh. 2.2 - Prob. 7ECh. 2.2 - Prob. 8ECh. 2.2 - Prob. 9ECh. 2.2 - Prob. 10ECh. 2.2 - Prob. 11ECh. 2.2 - Prob. 12ECh. 2.2 - Prob. 13ECh. 2.2 - Prob. 14ECh. 2.2 - Prob. 15ECh. 2.2 - Prob. 16ECh. 2.2 - Prob. 17ECh. 2.2 - Prob. 18ECh. 2.2 - Prob. 19ECh. 2.2 - Prob. 20ECh. 2.2 - Prob. 21ECh. 2.2 - Prob. 22ECh. 2.2 - Prob. 23ECh. 2.2 - Prob. 24ECh. 2.2 - Prob. 25ECh. 2.2 - Prob. 26ECh. 2.2 - Prob. 27ECh. 2.2 - Prob. 28ECh. 2.2 - Prob. 29ECh. 2.2 - Prob. 30ECh. 2.2 - Prob. 31ECh. 2.2 - Prob. 32ECh. 2.2 - Prob. 33ECh. 2.2 - Prob. 34ECh. 2.2 - Prob. 35ECh. 2.2 - Prob. 36ECh. 2.2 - Prob. 37ECh. 2.2 - Prob. 38ECh. 2.2 - Prob. 39ECh. 2.2 - Prob. 40ECh. 2.2 - Prob. 41ECh. 2.2 - Prob. 42ECh. 2.2 - Prob. 43ECh. 2.2 - Prob. 44ECh. 2.2 - Prob. 45ECh. 2.2 - Prob. 46ECh. 2.2 - Prob. 47ECh. 2.2 - Prob. 48ECh. 2.2 - Prob. 49ECh. 2.2 - Prob. 50ECh. 2.2 - Prob. 51ECh. 2.2 - Prob. 52ECh. 2.2 - Prob. 53ECh. 2.2 - Prob. 54ECh. 2.2 - Prob. 55ECh. 2.2 - Prob. 56ECh. 2.2 - Prob. 57ECh. 2.2 - Prob. 58ECh. 2.2 - Prob. 59ECh. 2.2 - Prob. 60ECh. 2.2 - Prob. 61ECh. 2.2 - Prob. 62ECh. 2.2 - Prob. 63ECh. 2.2 - Prob. 64ECh. 2.2 - Prob. 65ECh. 2.2 - Prob. 66ECh. 2.2 - Prob. 67ECh. 2.2 - Prob. 68ECh. 2.2 - Prob. 69ECh. 2.2 - Prob. 70ECh. 2.2 - Prob. 71ECh. 2.2 - Prob. 72ECh. 2.2 - Prob. 73ECh. 2.2 - Prob. 74ECh. 2.2 - Prob. 75ECh. 2.2 - Prob. 76ECh. 2.2 - Prob. 77ECh. 2.2 - Prob. 78ECh. 2.2 - Weather Balloon As a weather balloon is inflated,...Ch. 2.2 - Power from a Wind Turbine The power produced by a...Ch. 2.2 - Utility Rates Westside Energy charges its electric...Ch. 2.2 - Taxicab Function A taxi company charges 2.00 for...Ch. 2.2 - Prob. 83ECh. 2.2 - Prob. 84ECh. 2.2 - Prob. 85ECh. 2.2 - Prob. 86ECh. 2.2 - Prob. 87ECh. 2.3 - Prob. 1ECh. 2.3 - Prob. 2ECh. 2.3 - Prob. 3ECh. 2.3 - Prob. 4ECh. 2.3 - Prob. 5ECh. 2.3 - Prob. 6ECh. 2.3 - Prob. 7ECh. 2.3 - Prob. 8ECh. 2.3 - Prob. 9ECh. 2.3 - Prob. 10ECh. 2.3 - Prob. 11ECh. 2.3 - Prob. 12ECh. 2.3 - Prob. 13ECh. 2.3 - Prob. 14ECh. 2.3 - Prob. 15ECh. 2.3 - Prob. 16ECh. 2.3 - Prob. 17ECh. 2.3 - Prob. 18ECh. 2.3 - Prob. 19ECh. 2.3 - Prob. 20ECh. 2.3 - Prob. 21ECh. 2.3 - Prob. 22ECh. 2.3 - Prob. 23ECh. 2.3 - Prob. 24ECh. 2.3 - Prob. 25ECh. 2.3 - Prob. 26ECh. 2.3 - Prob. 27ECh. 2.3 - Prob. 28ECh. 2.3 - Prob. 29ECh. 2.3 - Prob. 30ECh. 2.3 - Prob. 31ECh. 2.3 - Prob. 32ECh. 2.3 - Prob. 33ECh. 2.3 - Prob. 34ECh. 2.3 - Prob. 35ECh. 2.3 - Prob. 36ECh. 2.3 - Prob. 37ECh. 2.3 - Prob. 38ECh. 2.3 - Prob. 39ECh. 2.3 - Prob. 40ECh. 2.3 - Prob. 41ECh. 2.3 - Prob. 42ECh. 2.3 - Prob. 43ECh. 2.3 - Earthquake The graph shows the vertical...Ch. 2.3 - Prob. 45ECh. 2.3 - Prob. 46ECh. 2.3 - Prob. 47ECh. 2.3 - Prob. 48ECh. 2.3 - Hurdle Race Three runners compete in a 100-meter...Ch. 2.3 - Gravity Near the Moon We can use Newtons Law of...Ch. 2.3 - Prob. 51ECh. 2.3 - Migrating Fish A fish swims at a speed v relative...Ch. 2.3 - Prob. 53ECh. 2.3 - Prob. 54ECh. 2.3 - Coughing When a foreign object that is lodged in...Ch. 2.3 - Prob. 56ECh. 2.3 - Prob. 57ECh. 2.3 - Prob. 58ECh. 2.4 - If you travel 100 miles in two hours, then your...Ch. 2.4 - The average rate of change of a function f between...Ch. 2.4 - The average rate of change of the function f(x) =...Ch. 2.4 - (a) The average rate of change of a function f...Ch. 2.4 - Prob. 5ECh. 2.4 - Prob. 6ECh. 2.4 - Prob. 7ECh. 2.4 - Prob. 8ECh. 2.4 - Prob. 9ECh. 2.4 - Prob. 10ECh. 2.4 - Prob. 11ECh. 2.4 - Prob. 12ECh. 2.4 - Prob. 13ECh. 2.4 - Prob. 14ECh. 2.4 - Prob. 15ECh. 2.4 - Prob. 16ECh. 2.4 - Prob. 17ECh. 2.4 - Prob. 18ECh. 2.4 - Prob. 19ECh. 2.4 - Prob. 20ECh. 2.4 - Prob. 21ECh. 2.4 - Prob. 22ECh. 2.4 - Changing Water Levels The graph shows the depth of...Ch. 2.4 - Population Growth and Decline The graph shows the...Ch. 2.4 - Population Growth and Decline The table gives the...Ch. 2.4 - Running Speed A man is running around a circular...Ch. 2.4 - Prob. 27ECh. 2.4 - Book Collection Between 1980 and 2000 a rare book...Ch. 2.4 - Cooling Soup When a bowl of hot soup is left in a...Ch. 2.4 - Farms in the United States The graph gives the...Ch. 2.4 - Prob. 31ECh. 2.4 - Prob. 32ECh. 2.4 - Prob. 33ECh. 2.5 - Fill in the blank with the appropriate direction...Ch. 2.5 - Prob. 2ECh. 2.5 - Prob. 3ECh. 2.5 - Prob. 4ECh. 2.5 - Prob. 5ECh. 2.5 - Prob. 6ECh. 2.5 - Prob. 7ECh. 2.5 - Prob. 8ECh. 2.5 - Prob. 9ECh. 2.5 - Prob. 10ECh. 2.5 - Prob. 11ECh. 2.5 - Prob. 12ECh. 2.5 - Prob. 13ECh. 2.5 - Prob. 14ECh. 2.5 - Prob. 15ECh. 2.5 - Prob. 16ECh. 2.5 - Prob. 17ECh. 2.5 - Prob. 18ECh. 2.5 - Prob. 19ECh. 2.5 - Prob. 20ECh. 2.5 - Prob. 21ECh. 2.5 - Prob. 22ECh. 2.5 - Prob. 23ECh. 2.5 - Prob. 24ECh. 2.5 - Prob. 25ECh. 2.5 - Prob. 26ECh. 2.5 - Prob. 27ECh. 2.5 - Prob. 28ECh. 2.5 - Prob. 29ECh. 2.5 - Prob. 30ECh. 2.5 - Prob. 31ECh. 2.5 - Prob. 32ECh. 2.5 - Prob. 33ECh. 2.5 - Prob. 34ECh. 2.5 - Prob. 35ECh. 2.5 - Prob. 36ECh. 2.5 - Prob. 37ECh. 2.5 - Prob. 38ECh. 2.5 - Prob. 39ECh. 2.5 - Prob. 40ECh. 2.5 - Prob. 41ECh. 2.5 - Prob. 42ECh. 2.5 - Prob. 43ECh. 2.5 - Prob. 44ECh. 2.5 - Prob. 45ECh. 2.5 - Prob. 46ECh. 2.5 - Prob. 47ECh. 2.5 - Prob. 48ECh. 2.5 - Prob. 49ECh. 2.5 - Prob. 50ECh. 2.5 - Prob. 51ECh. 2.5 - Prob. 52ECh. 2.5 - Prob. 53ECh. 2.5 - Prob. 54ECh. 2.5 - Prob. 55ECh. 2.5 - Prob. 56ECh. 2.5 - Prob. 57ECh. 2.5 - Prob. 58ECh. 2.5 - Prob. 59ECh. 2.5 - Prob. 60ECh. 2.5 - Prob. 61ECh. 2.5 - Prob. 62ECh. 2.5 - Prob. 63ECh. 2.5 - Prob. 64ECh. 2.5 - Prob. 65ECh. 2.5 - Prob. 66ECh. 2.5 - Prob. 67ECh. 2.5 - Prob. 68ECh. 2.5 - Prob. 69ECh. 2.5 - Prob. 70ECh. 2.5 - Prob. 71ECh. 2.5 - Prob. 72ECh. 2.5 - Prob. 73ECh. 2.5 - Prob. 74ECh. 2.5 - Prob. 75ECh. 2.5 - Prob. 76ECh. 2.5 - Prob. 77ECh. 2.5 - Prob. 78ECh. 2.5 - Prob. 79ECh. 2.5 - Prob. 80ECh. 2.5 - Prob. 81ECh. 2.5 - Prob. 82ECh. 2.5 - Prob. 83ECh. 2.5 - Prob. 84ECh. 2.5 - Prob. 85ECh. 2.5 - Prob. 86ECh. 2.5 - Prob. 87ECh. 2.5 - Prob. 88ECh. 2.5 - Prob. 89ECh. 2.5 - Prob. 90ECh. 2.5 - Prob. 91ECh. 2.5 - Prob. 92ECh. 2.5 - Prob. 93ECh. 2.6 - From the graphs of f and g in the figure, we find...Ch. 2.6 - By definition, (f g)(x) = _____. So if g(2) = 5...Ch. 2.6 - If the rule of the function f is add one and the...Ch. 2.6 - We can express the functions in Exercise 3...Ch. 2.6 - Prob. 5ECh. 2.6 - Prob. 6ECh. 2.6 - Prob. 7ECh. 2.6 - Prob. 8ECh. 2.6 - Prob. 9ECh. 2.6 - Prob. 10ECh. 2.6 - Prob. 11ECh. 2.6 - Prob. 12ECh. 2.6 - Prob. 13ECh. 2.6 - Prob. 14ECh. 2.6 - Prob. 15ECh. 2.6 - Prob. 16ECh. 2.6 - Prob. 17ECh. 2.6 - Prob. 18ECh. 2.6 - Prob. 19ECh. 2.6 - Prob. 20ECh. 2.6 - Prob. 21ECh. 2.6 - Prob. 22ECh. 2.6 - Prob. 23ECh. 2.6 - Prob. 24ECh. 2.6 - Prob. 25ECh. 2.6 - Prob. 26ECh. 2.6 - Prob. 27ECh. 2.6 - Prob. 28ECh. 2.6 - Prob. 29ECh. 2.6 - Prob. 30ECh. 2.6 - Prob. 31ECh. 2.6 - Prob. 32ECh. 2.6 - Prob. 33ECh. 2.6 - Prob. 34ECh. 2.6 - Prob. 35ECh. 2.6 - Prob. 36ECh. 2.6 - Prob. 37ECh. 2.6 - Prob. 38ECh. 2.6 - Prob. 39ECh. 2.6 - Prob. 40ECh. 2.6 - Prob. 41ECh. 2.6 - Prob. 42ECh. 2.6 - Prob. 43ECh. 2.6 - Prob. 44ECh. 2.6 - Prob. 45ECh. 2.6 - Prob. 46ECh. 2.6 - Prob. 47ECh. 2.6 - Prob. 48ECh. 2.6 - Prob. 49ECh. 2.6 - Prob. 50ECh. 2.6 - Prob. 51ECh. 2.6 - Prob. 52ECh. 2.6 - Prob. 53ECh. 2.6 - Prob. 54ECh. 2.6 - Prob. 55ECh. 2.6 - Prob. 56ECh. 2.6 - Prob. 57ECh. 2.6 - Prob. 58ECh. 2.6 - Prob. 59ECh. 2.6 - Revenue, Cost, and Profit A print shop makes...Ch. 2.6 - Area of a Ripple A stone is dropped in a lake,...Ch. 2.6 - Inflating a Balloon A spherical balloon is being...Ch. 2.6 - Area of a Balloon A spherical weather balloon is...Ch. 2.6 - Multiple Discounts You have a 50 coupon from the...Ch. 2.6 - Multiple Discounts An appliance dealer advertises...Ch. 2.6 - Airplane Trajectory An airplane is flying at a...Ch. 2.6 - Prob. 67ECh. 2.6 - Prob. 68ECh. 2.6 - Prob. 69ECh. 2.6 - Prob. 70ECh. 2.7 - A function f is one-to-one if different inputs...Ch. 2.7 - (a) For a function to have an inverse, it must be...Ch. 2.7 - A function f has the following verbal description:...Ch. 2.7 - True or false? (a) If f has an inverse, then f1(x)...Ch. 2.7 - Prob. 5ECh. 2.7 - Prob. 6ECh. 2.7 - Prob. 7ECh. 2.7 - Prob. 8ECh. 2.7 - Prob. 9ECh. 2.7 - Prob. 10ECh. 2.7 - Prob. 11ECh. 2.7 - Prob. 12ECh. 2.7 - Prob. 13ECh. 2.7 - Prob. 14ECh. 2.7 - Prob. 15ECh. 2.7 - Prob. 16ECh. 2.7 - Prob. 17ECh. 2.7 - Prob. 18ECh. 2.7 - Prob. 19ECh. 2.7 - Prob. 20ECh. 2.7 - Prob. 21ECh. 2.7 - Prob. 22ECh. 2.7 - Prob. 23ECh. 2.7 - Prob. 24ECh. 2.7 - Prob. 25ECh. 2.7 - Prob. 26ECh. 2.7 - Prob. 27ECh. 2.7 - Prob. 28ECh. 2.7 - Prob. 29ECh. 2.7 - Prob. 30ECh. 2.7 - Prob. 31ECh. 2.7 - Prob. 32ECh. 2.7 - Prob. 33ECh. 2.7 - Prob. 34ECh. 2.7 - Prob. 35ECh. 2.7 - Prob. 36ECh. 2.7 - Prob. 37ECh. 2.7 - Prob. 38ECh. 2.7 - Prob. 39ECh. 2.7 - Prob. 40ECh. 2.7 - Prob. 41ECh. 2.7 - Prob. 42ECh. 2.7 - Prob. 43ECh. 2.7 - Prob. 44ECh. 2.7 - Prob. 45ECh. 2.7 - Prob. 46ECh. 2.7 - Prob. 47ECh. 2.7 - Prob. 48ECh. 2.7 - Prob. 49ECh. 2.7 - Prob. 50ECh. 2.7 - Prob. 51ECh. 2.7 - Prob. 52ECh. 2.7 - Prob. 53ECh. 2.7 - Prob. 54ECh. 2.7 - Prob. 55ECh. 2.7 - Prob. 56ECh. 2.7 - Prob. 57ECh. 2.7 - Prob. 58ECh. 2.7 - Prob. 59ECh. 2.7 - Prob. 60ECh. 2.7 - Prob. 61ECh. 2.7 - Prob. 62ECh. 2.7 - Prob. 63ECh. 2.7 - Prob. 64ECh. 2.7 - Prob. 65ECh. 2.7 - Prob. 66ECh. 2.7 - Prob. 67ECh. 2.7 - Prob. 68ECh. 2.7 - Prob. 69ECh. 2.7 - Prob. 70ECh. 2.7 - Prob. 71ECh. 2.7 - Prob. 72ECh. 2.7 - Prob. 73ECh. 2.7 - Prob. 74ECh. 2.7 - Prob. 75ECh. 2.7 - Prob. 76ECh. 2.7 - Prob. 77ECh. 2.7 - Prob. 78ECh. 2.7 - Prob. 79ECh. 2.7 - Prob. 80ECh. 2.7 - Fee for Service For his services, a private...Ch. 2.7 - Prob. 82ECh. 2.7 - Prob. 83ECh. 2.7 - Prob. 84ECh. 2.7 - Prob. 85ECh. 2.7 - Prob. 86ECh. 2.7 - Income Tax In a certain country the tax on incomes...Ch. 2.7 - Prob. 88ECh. 2.7 - Prob. 89ECh. 2.7 - Prob. 90ECh. 2.7 - Prob. 91ECh. 2.7 - Prob. 92ECh. 2.7 - Prob. 93ECh. 2 - Prob. 1RCCCh. 2 - Prob. 2RCCCh. 2 - Prob. 3RCCCh. 2 - Prob. 4RCCCh. 2 - Prob. 5RCCCh. 2 - Prob. 6RCCCh. 2 - Prob. 7RCCCh. 2 - Prob. 8RCCCh. 2 - Prob. 9RCCCh. 2 - Prob. 10RCCCh. 2 - Prob. 11RCCCh. 2 - Prob. 12RCCCh. 2 - Prob. 1RECh. 2 - Prob. 2RECh. 2 - Prob. 3RECh. 2 - Prob. 4RECh. 2 - Prob. 5RECh. 2 - Prob. 6RECh. 2 - Prob. 7RECh. 2 - Prob. 8RECh. 2 - Prob. 9RECh. 2 - Prob. 10RECh. 2 - Prob. 11RECh. 2 - Prob. 12RECh. 2 - Prob. 13RECh. 2 - Prob. 14RECh. 2 - Prob. 15RECh. 2 - Prob. 16RECh. 2 - Prob. 17RECh. 2 - Prob. 18RECh. 2 - Prob. 19RECh. 2 - Prob. 20RECh. 2 - Prob. 21RECh. 2 - Prob. 22RECh. 2 - Prob. 23RECh. 2 - Prob. 24RECh. 2 - Prob. 25RECh. 2 - Prob. 26RECh. 2 - Prob. 27RECh. 2 - Prob. 28RECh. 2 - Prob. 29RECh. 2 - Prob. 30RECh. 2 - Prob. 31RECh. 2 - Prob. 32RECh. 2 - Prob. 33RECh. 2 - Prob. 34RECh. 2 - Prob. 35RECh. 2 - Prob. 36RECh. 2 - Prob. 37RECh. 2 - Prob. 38RECh. 2 - Prob. 39RECh. 2 - Prob. 40RECh. 2 - Prob. 41RECh. 2 - Prob. 42RECh. 2 - Prob. 43RECh. 2 - Prob. 44RECh. 2 - Prob. 45RECh. 2 - Prob. 46RECh. 2 - Prob. 47RECh. 2 - Prob. 48RECh. 2 - Prob. 49RECh. 2 - Prob. 50RECh. 2 - Prob. 51RECh. 2 - Prob. 52RECh. 2 - Prob. 53RECh. 2 - Prob. 54RECh. 2 - Prob. 55RECh. 2 - Prob. 56RECh. 2 - Prob. 57RECh. 2 - Prob. 58RECh. 2 - Prob. 59RECh. 2 - Prob. 60RECh. 2 - Prob. 61RECh. 2 - Prob. 62RECh. 2 - Prob. 63RECh. 2 - Prob. 64RECh. 2 - Prob. 65RECh. 2 - Prob. 66RECh. 2 - Prob. 67RECh. 2 - Prob. 68RECh. 2 - Prob. 69RECh. 2 - Prob. 70RECh. 2 - Prob. 71RECh. 2 - Prob. 72RECh. 2 - Prob. 73RECh. 2 - Prob. 74RECh. 2 - Prob. 75RECh. 2 - Prob. 76RECh. 2 - Prob. 77RECh. 2 - Prob. 78RECh. 2 - Prob. 79RECh. 2 - Prob. 80RECh. 2 - Prob. 81RECh. 2 - Prob. 82RECh. 2 - Prob. 83RECh. 2 - Prob. 84RECh. 2 - Prob. 85RECh. 2 - Prob. 86RECh. 2 - Prob. 87RECh. 2 - Prob. 88RECh. 2 - Prob. 89RECh. 2 - Prob. 90RECh. 2 - Prob. 91RECh. 2 - Prob. 92RECh. 2 - Prob. 1TCh. 2 - Prob. 2TCh. 2 - A function f has the following verbal description:...Ch. 2 - A school fund-raising group sells chocolate bars...Ch. 2 - Prob. 5TCh. 2 - Prob. 6TCh. 2 - Prob. 7TCh. 2 - Prob. 8TCh. 2 - Prob. 9TCh. 2 - Prob. 10TCh. 2 - Prob. 11TCh. 2 - Prob. 12TCh. 2 - Prob. 1PCh. 2 - Prob. 2PCh. 2 - Prob. 3PCh. 2 - Prob. 4PCh. 2 - Prob. 5PCh. 2 - Prob. 6PCh. 2 - Prob. 7PCh. 2 - Prob. 8PCh. 2 - Prob. 9PCh. 2 - Prob. 10PCh. 2 - Prob. 11PCh. 2 - Length A woman 5 ft tall is standing near a street...Ch. 2 - Distance Two ships leave port at the same time....Ch. 2 - Prob. 14PCh. 2 - Area An isosceles triangle has a perimeter of 8...Ch. 2 - Prob. 16PCh. 2 - Area A rectangle is inscribed in a semicircle of...Ch. 2 - Height The volume of a cone is 100 in3. Find a...Ch. 2 - Prob. 19PCh. 2 - Minimizing a Sum Find two positive numbers whose...Ch. 2 - Prob. 21PCh. 2 - Dividing a Pen A rancher with 750 ft of fencing...Ch. 2 - Fencing a Garden Plot A property owner wants to...Ch. 2 - Maximizing Area A wire 10 cm long is cut into two...Ch. 2 - Light from a Window A Norman window has the shape...Ch. 2 - Volume of a Box A box with an open top is to be...Ch. 2 - Area of a Box An open box with a square base is to...Ch. 2 - Inscribed Rectangle Find the dimensions that give...Ch. 2 - Minimizing Costs A rancher wants to build a...Ch. 2 - Minimizing Time A man stands at a point A on the...Ch. 2 - Bird Flight A bird is released from point A on an...Ch. 2 - Area of a Kite A kite frame is to be made from six...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Calculus lll May I please have the solutions for the following examples? Thank youarrow_forwardCalculus lll May I please have the solutions for the following exercises that are blank? Thank youarrow_forwardThe graph of 2(x² + y²)² = 25 (x²-y²), shown in the figure, is a lemniscate of Bernoulli. Find the equation of the tangent line at the point (3,1). -10 Write the expression for the slope in terms of x and y. slope = 4x³ + 4xy2-25x 2 3 4x²y + 4y³ + 25y Write the equation for the line tangent to the point (3,1). LV Q +arrow_forward
- Find the equation of the tangent line at the given value of x on the curve. 2y3+xy-y= 250x4; x=1 y=arrow_forwardFind the equation of the tangent line at the given point on the curve. 3y² -√x=44, (16,4) y=] ...arrow_forwardFor a certain product, cost C and revenue R are given as follows, where x is the number of units sold in hundreds. Cost: C² = x² +92√x+56 Revenue: 898(x-6)² + 24R² = 16,224 dC a. Find the marginal cost at x = 6. dx The marginal cost is estimated to be $ ☐ . (Do not round until the final answer. Then round to the nearest hundredth as needed.)arrow_forward
- The graph of 3 (x² + y²)² = 100 (x² - y²), shown in the figure, is a lemniscate of Bernoulli. Find the equation of the tangent line at the point (4,2). АУ -10 10 Write the expression for the slope in terms of x and y. slope =arrow_forwardUse a geometric series to represent each of the given functions as a power series about x=0, and find their intervals of convergence. a. f(x)=5/(3-x) b. g(x)= 3/(x-2)arrow_forwardAn object of mass 4 kg is given an initial downward velocity of 60 m/sec and then allowed to fall under the influence of gravity. Assume that the force in newtons due to air resistance is - 8v, where v is the velocity of the object in m/sec. Determine the equation of motion of the object. If the object is initially 500 m above the ground, determine when the object will strike the ground. Assume that the acceleration due to gravity is 9.81 m/sec² and let x(t) represent the distance the object has fallen in t seconds. Determine the equation of motion of the object. x(t) = (Use integers or decimals for any numbers in the expression. Round to two decimal places as needed.)arrow_forward
- Early Monday morning, the temperature in the lecture hall has fallen to 40°F, the same as the temperature outside. At 7:00 A.M., the janitor turns on the furnace with the thermostat set at 72°F. The time constant for the building is = 3 hr and that for the building along with its heating system is 1 K A.M.? When will the temperature inside the hall reach 71°F? 1 = 1 hr. Assuming that the outside temperature remains constant, what will be the temperature inside the lecture hall at 8:30 2 At 8:30 A.M., the temperature inside the lecture hall will be about (Round to the nearest tenth as needed.) 1°F.arrow_forwardFind the maximum volume of a rectangular box whose surface area is 1500 cm² and whose total edge length is 200 cm. cm³arrow_forwardFind the minimum cost of a rectangular box of volume 120 cm³ whose top and bottom cost 6 cents per cm² and whose sides cost 5 cents per cm². Round your answer to nearest whole number cents. Cost = cents.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Differential Equation | MIT 18.01SC Single Variable Calculus, Fall 2010; Author: MIT OpenCourseWare;https://www.youtube.com/watch?v=HaOHUfymsuk;License: Standard YouTube License, CC-BY