
Concept explainers
How many moles of electrons are required to produce (a) 0.84 L of O2 at exactly 1 atm and 25°C from aqueous H2SO4 solution; (b) 1.50 L of Cl2 at 750 mmHg and 20°C from molten NaCl; (c) 6.0 g of Sn from molten SnCl2?
(a)
Interpretation:
Need to calculate the Faraday of electricity needed for the production of 0.84L of O2 with 1 atm pressure upon electrolysis of aqueous H2SO4 at 25oC.
Concept introduction:
Electrolysis of aqueous sulfuric acid i.e. acidified water resulted in the production of oxygen and hydrogen gas, which will be liberated at the anode and cathode respectively. The presence of H+ and SO-4 made the solution to be more conductivity. SO-4 is more stable to be inert at the anode.
Further the cell reaction can be written as shown below
Since volume and pressure of oxygen produced was given, by applying it into ideal gas equation we can calculate the number of mole of oxygen produced
The ideal gas equation can be given as follows.
On applying the number of moles of oxygen produced into stoichiometry of the reaction, the number of moles electron involved in the reaction can be calculated. In case of the given reaction 4 mole of electron was liberated during the production of one mole of oxygen. Since one Faraday is equal to one mole of electron, so 4 Faraday of electricity will be needed to produce one mole of oxygen.
Finally the Faraday of electricity utilized to produce the required amount of oxygen can be calculated according the formula
To find: Amount of Faraday of electricity need to produce 0.076L of O2 with pressure 755mmHg, at 298K, through electrolysis of water.
Answer to Problem 18.52QP
Ideal gas equation can be used to calculate the number of moles of oxygen produced, from that faraday of electricity needed will be calculated in successive steps (a)
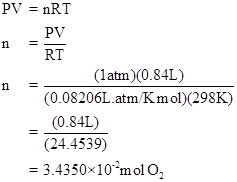
Since one mole of oxygen need 4 Faraday of electricity, so the Faraday of electricity needed to produce
Faraday of electricity need to produce 0.84L of oxygen with pressure 1 atm was calculated as
Explanation of Solution
Ideal gas equation can be used to calculate the number of moles of oxygen produced
Since one mole of oxygen need 4 Faraday of electricity, so the Faraday of electricity needed to produce
Faraday of electricity need to produce 0.84L of oxygen with pressure 1 atm was calculated as
At first the number of moles of oxygen produced through electrolysis was calculated using ideal gas equation, from the given volume and pressure. Thus it was calculated as
The amount of electricity needed to produce 0.84L of oxygen with pressure of 1atm was determined to be
(b)
Interpretation:
Need to calculate the Faraday of electricity needed for the production of 1.50L of Cl2 with pressure 750 mmHg at 20oC by electrolysis of molten NaCl.
Concept introduction:
Electrolysis of molten sodium chloride was represented by the below equation. By using ideal gas equation, the number of moles of chlorine liberated at the anode can be calculated, provided the pressure and volume are known.
The ideal gas equation can be given as follows.
The equation we find that two mole of electron is needed to produce one mole of chlorine gas , Since one Faraday is equal to one mole of electron, The Faraday of electricity utilized to produce given amount of chlorine can be calculated according the formula
To find: Faraday of electricity need to produce 1.50 L of Cl2 with pressure 750mmHg, at 293K, through electrolysis of molten NaCl.
Answer to Problem 18.52QP
Ideal gas equation can be used to calculate the number of moles of chlorine gas produced, Further from the number of moles of chlorine; the faraday of electricity utilized will be calculated in successive steps (b)
Since one mole of chlorine need two Faraday of electricity, so the Faraday of electricity needed to produce
Faraday of electricity need to produce 1.50L of chlorine with pressure 750mm Hg was calculated as
Explanation of Solution
Ideal gas equation can be used to calculate the number of moles of oxygen produced
Since one mole of chlorine need two Faraday of electricity, so the Faraday of electricity needed to produce
The number of moles of chlorine produced through electrolysis was calculated using ideal gas equation, from the given volume and pressure it was calculated as
The amount of electricity needed to produce 1.5 L of chlorine with pressure of 750 mmHg was determined to be
(c)
Interpretation:
Need to calculate the Faraday of electricity needed for the production of 6g of Sn though electrolysis of molten SnCl2.
Concept introduction:
Electrolysis of molten stannous chloride will result in the formation of Tin (Sn) and chlorine gas and half-cell reaction at the anode and cathode was given below. In this two electrons were released by chloride ion at the anode and get liberated as chlorine gas, further stannous ion accept two electron and for tin metal
The ideal gas equation can be given as follows.
Since the mass of the metal produced was given, from that number of moles of Sn can be calculated. Further from the number of moles of Sn produced the Faraday of electricity can be calculated by the formula given below, since one Faraday is equal to one mole of electron. In the present case 2 moles of electrons are needed to reduce one mole of Sn2+
So
To find: Faraday of electricity need to produce 6 g of Tin, by electrolysis of molten SnCl2.
Answer to Problem 18.52QP
From the mass of tin produced during the electrolysis, the Faraday of electricity needed for reaction can be calculated in the following steps (c).
Since one mole of Sn2+ ion need two Faraday of electricity to, so the Faraday of electricity needed to produce
Explanation of Solution
From the molar mass calculation
Weight = 6g
Atomic Mass = 118.7g
Since one mole of Sn2+ ion need two Faraday of electricity, so the Faraday of electricity needed to produce
The number of moles of tin produced through electrolysis was calculated as
The Faraday of electricity need to produce 6g of Tin from by electrolysis of molten SnCl2 was identified as
Want to see more full solutions like this?
Chapter 18 Solutions
CHEMISTRY (LL) W/CNCT >BI<
- Give the organic products: (benzyne) Br ? CH3 + K* :NH, liq NH3 HINT: Two products are formed. Each is a substituted aniline; they are isomers of each other. NH2 II I H₂N. CH3 CH3 III Select one: ○ A. I and II ○ B. I and III O C. I and IV O D. II and III O E. III and IV H₂N CH3 IV CH₂-NH2arrow_forwardPredict the major products of this organic reaction: HBr (1 equiv) cold ? Some important notes: • Draw the major product, or products, of this reaction in the drawing area below. • You can draw the products in any arrangement you like. • Pay careful attention to the reaction conditions, and only include the major products. • Be sure to use wedge and dash bonds when necessary, for example to distinguish between major products that are enantiomers. • Note that there is only 1 equivalent of HBr reactant, so you need not consider the case of multiple additions. Erase something Explanation Check 2025 McGraw Hill LLC. All Rights Reserved. Terarrow_forwardQ14. Fill this chart: (please refer to ppt notes/browser to answer these questions) What alcohol is also called wood alcohol? What is the common name of ethanol? Draw the structure of phenol and thiophene? Are bigger chain alcohol like heptanol and octanol are soluble or insoluble in water and explain it ? Are ethers soluble or insoluble in water? What suffix and prefix are used for alcohol while naming alcohol and ether? What the process called when we add water to any alkene to make alcohol? Q16. Draw the diagram of following aromatic compound (practice from previous module) Aniline Phenol Benzoic acid Methyl benzoate Q17. a. Write the oxidation reactions for the 2 propanol. b. Write the oxidation reaction of the ethanol.arrow_forward
- Question 11 of 18 (1 point) Question Attempt: 3 of How many signals do you expect in the 'H NMR spectrum for this molecule? Br Br Write the answer below. Also, in each of the drawing areas below is a copy of the molecule, with Hs shown. In each copy, one of the H atoms is colored red. Highlight in red all other H atoms that would contribute to the same signal as the H already highlighted red. Note for advanced students: In this question, any multiplet is counted as one signal. Number of signals in the 'H NMR spectrum. 1 For the molecule in the top drawing area, highlight in red any other H atoms that will contribute to the same signal as the H atom already highlighted red. If no other H atoms will contribute, check the box at right. No additional Hs to color in top molecule Check For the molecule in the bottom drawing area, highlight in red any other H atoms that will contribute to the same signal as the H atom already highlighted red. If no other H atoms will contribute, check the box…arrow_forwardOrganic Chemistry Esterification reactions 1. Write the steps to prepare ester. 2. Write complete reaction of ethanol and acetic acid to make ester. 3. What does ester smell like? What are the uses of ester. 4. What the role of sulfuric acid in the esterification reactionarrow_forward11. Complete the following esterification reaction with names of all the reactants and products under. Hint: Remove the water and end up with ester R-C-OH + ROH R-C-OR + H₂O A carboxylic acid An alcohol An ester Water BYJU'S H-C-C O-H Нин C-C-C-H HAAA H O-C-C-C-H AAA Ethanoic acid Propanol Water Propyl ethanoate By com CH3COOH + CH3CH2CH2CH₂CH₂OH → Practice for alcohols aldehydes and ketones: 12. Draw the structures from the following names mixed of alcohol/aldehyde and ketone: a. 4-methyl cyclohexanone b. 3-methyl-2-pentenal c. 2,3-dimethylcyclohexanone d. 1,3propanediol or Propane 1,3 diol 13. Write systematic names for the following compounds identify functional group: a. b. (CH3)2CH-C OH c) CH(CH₂)-- OH -,-,arrow_forward
- may you please show all steps! i am having a hard time understanding and applying in this format, thank you!arrow_forward10. Complete the substitution reaction of 2 pentanol with these reagents. Reagents & Reaction Conditions use practice sheet. Please write only major products, minor product like water, other gases are not required. Hint: In substitution of alcohol, we generally substitute OH group with Halogens like cl, Br, F using some reagent containing halogens. Ensure to add halogens to the same carbon number where you are removing OH from Examples Alcohols can be converted to Alkyl Halides with HX acids HBr H₂O HCI + H₂O HI + H₂O CH,CH₂OH + SOCI₂ CH,CH₂OH + PCI₁₂ A BBYJU'S CH CHCI + SO₂+ HCI CH₂CH CIP(OH), + HCI CH,CH₂OH + PCI CHCHCI + POCI + HCI CH,CH₂OH + PBr, CH,CH,Br + P(OH), + HBr 1. Reaction with HBr with 2 Pentanol 2.Reaction with HI with 2 pentanol © Byjus.com 3.Reaction with HCI+ZnCl,, with 2 pentanol (Zncl2 is catalyst no role) 4.Reaction with SOCI,, with 2 Pentanol 5.Reaction with PBr; or PCl, with 2 pentanolarrow_forward3. Is 2-methyl-2-propanol a primary, secondary, or tertiary alcohol? Write out the structures of 2-methyl-2-propanol and also any oxidation products of 2- methyl-2- propanol. If there is more than one oxidation product, give the structure of each of the products. 4. 2-Propanol is the IUPAC systematic name of this alcohol. It has a common name by which it is much better known (You'll see it in the grocery store or pharmacy). Give that common name 5. Aldehydes can be synthesized by the oxidation of. Please choose from below choices A. Primary alcohols B. Secondary alcohols C. Organic acids D. Inorganic acids 6. Tertiary alcohol Can undergo oxidation. yes or no. ? If yes then answer the product.arrow_forward
- Finish the reactions hand written pleasearrow_forwardPart A Identify each alcohol as primary, secondary, or tertiary Drag the appropriate items to their respective bins. CH₂ H₂C- -C-OH HO CH₂ Primary Он OH CH₂ OH CCH₂OH CH₂ сн Secondary Tertiary Reset Help CH,CH₂ (CH)CHCH,OH CH,CH,CH,CCH, CHOH CH₂ Different types of alcohol groups Alcohol and its reaction: 8. Combing two alcohol molecules below and completing the reaction with Product .( Hint Reaction called etherification as ether is formed and name the ether once you complete the reaction. Hint.: R-O-H+H-O-RR-O-R Do the reaction: CH₂OH + CH₂OH---→ + H-O-H 9. Write the reaction of formation of alcohol from alkene by adding water: Addition reaction also called hydration reaction as we are adding water which occur always in presence of acid Hint: Break the double bond and add H and OH if symmetrical then add anywhere if unsymmetrical then follow Markovnikov rule H should go to that double bone carbon which has more hydrogen CH2=CH2 + H₂O-→arrow_forwardComplete the reaction hand written pleasearrow_forward
 Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning
Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning Chemistry by OpenStax (2015-05-04)ChemistryISBN:9781938168390Author:Klaus Theopold, Richard H Langley, Paul Flowers, William R. Robinson, Mark BlaserPublisher:OpenStax
Chemistry by OpenStax (2015-05-04)ChemistryISBN:9781938168390Author:Klaus Theopold, Richard H Langley, Paul Flowers, William R. Robinson, Mark BlaserPublisher:OpenStax Principles of Modern ChemistryChemistryISBN:9781305079113Author:David W. Oxtoby, H. Pat Gillis, Laurie J. ButlerPublisher:Cengage Learning
Principles of Modern ChemistryChemistryISBN:9781305079113Author:David W. Oxtoby, H. Pat Gillis, Laurie J. ButlerPublisher:Cengage Learning Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage LearningChemistry: Matter and ChangeChemistryISBN:9780078746376Author:Dinah Zike, Laurel Dingrando, Nicholas Hainen, Cheryl WistromPublisher:Glencoe/McGraw-Hill School Pub Co
Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage LearningChemistry: Matter and ChangeChemistryISBN:9780078746376Author:Dinah Zike, Laurel Dingrando, Nicholas Hainen, Cheryl WistromPublisher:Glencoe/McGraw-Hill School Pub Co Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning
Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning





