
Find the factor of safety against overturning, sliding, and bearing capacity.
Answer to Problem 17.1P
The factor of safety against overturning is
The factor of safety against sliding is
The factor of safety against bearing capacity failure is
Explanation of Solution
Given information:
The frictional angle of backfill
Unit weight of backfill
The backfill makes an angle of
Unit weight of concrete is
Calculation:
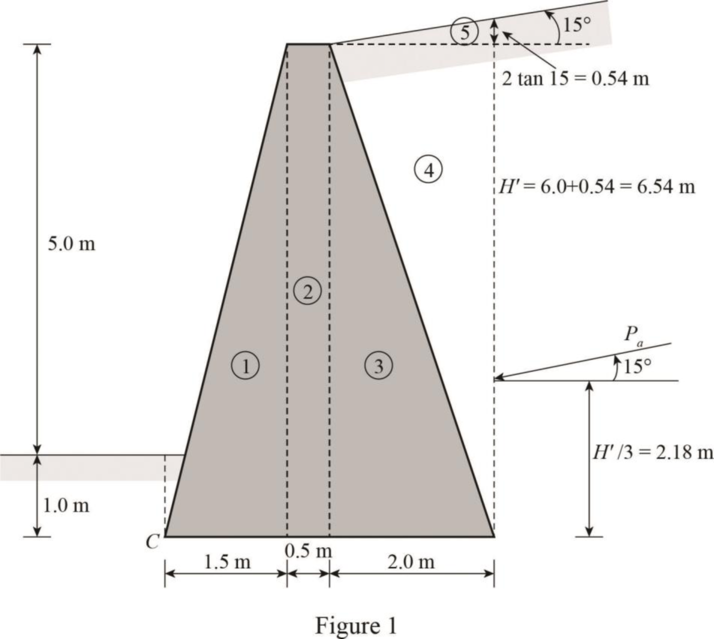
Calculate the weight and moment arms by dividing the retaining wall and soil regions interest into rectangles and triangles.
Show the rectangles and triangles divided in the structure as in Figure 1.
Refer Table 16.3, “Values of
The value of active earth pressure
From Figure 1.
The total height from base is
Find the total force per unit length of the wall
Substitute
Find the horizontal force
Substitute
Find the vertical force
Substitute
Find the weight and moment about C for the sections as in Table 1.
| Section |
Weight |
Moment arm from C (m) |
Moment about C |
| 1 | 1 | 108 | |
| 2 | 1.75 | 126 | |
| 3 | 2.67 | 384.5 | |
| 4 | 3.33 | 369.6 | |
| 5 | 3.33 | 33.3 | |
| 4 | 121.6 | ||
Analyze the stability with respect to overturning:
Find the overturning moment
Substitute
From Table 1, the value of resisting moment is
Find the factor of safety against overturning using the relation:
Substitute
Therefore, the factor of safety against overturning is
Find the passive earth pressure coefficient
Substitute
Find the passive force
Here, D is the depth of retaining wall below the soil.
Substitute
Find the value of
Substitute
Find the factor of safety against sliding using the relation:
Substitute
Therefore, the factor of safety against sliding is
Analyze the stability with respect to bearing capacity failure:
Find the eccentricity (e) of the resulting force using the relation:
Here, B is the base width of the retaining wall.
Substitute 4 m for B,
The value of
The calculated eccentricity value is less than the value of
Find the maximum value of pressure at
Substitute
Find the ultimate bearing capacity
Find the value of
Substitute
Find the value of
Substitute 4 m for B and 0.116 m for e.
Refer Table 6.2, “Bearing capacity factors” in the textbook.
The value of
Find the depth factor
Substitute
For
Find the inclination of load on the foundation with respect to vertical
Substitute
Find the inclination factor
Substitute
Find the inclination factor
Substitute
Substitute
Find the factor of safety against bearing capacity failure using the relation:
Substitute
Therefore, the factor of safety against bearing capacity failure is
Want to see more full solutions like this?
Chapter 17 Solutions
Principles Of Foundation Engineering 9e
- Determine the stiffness matrices of elements 2, 3 and 4 in the global co-ordinate system. Assume A=0.0015m2 and E=200GPa, indicate the degrees of freedom in all stiffness matricies.arrow_forwardA short plain concrete column with cross-section dimensions of 12 in x 12 in is to be constructed. If the compressive strength of the concrete (f’c) is 5000 psi, what is the maximum load that can be safely applied to the column? - 600 k - 950 k - 720 k - 347 karrow_forwardThe borrow pit has 2000 cyds of suitable fill. The fill required for the project is 1900 cyds. The swell factor is 10% and the shrinkage factor is 15%. How much more borrow do we need? Or is there extra? - 13 yards extra - 13 yards short - 200 yards extra - 161 yards shortarrow_forward
- The job site has a primary vertical control point with a reference benchmark of 100 ft. An instrument is set up with an HI of 5.42 ft above the BM. A grade stake is set at an elevation of 96 ft. What is the height reading on the rod at the grade stake? - 9.42 ft - 4.00 ft - 1.42 ft - 5.42 ftarrow_forwardAssume you have a simple beam 16 ft long supported on each end by R1 and R2. There is a concentrated load of 900 lb that is 4 ft from R2. Reaction R1 is pinned 12 ft from the load. Reaction R1 is 225 lb and R2 is 675 lb. What is the maximum bending moment in pounds per foot? - 3,600 - 1,800 - 2,700- 900arrow_forwardA wall form is four-feet high, ten-feet long and ten-feet wide. It is full of fluid concrete. What is the pressure at the bottom of the form? - 86,400 psi - 60,000 psf - 600 psf - 60,000 psiarrow_forward
- he sides of a building are 300 feet long and 200 feet wide. What is the diagonal distance between the opposite corners? - 300 feet - 306 feet - 360.60 feet - 306.6 feetarrow_forwardThe excavation for a square basement requires a 1:2 H:V slope cut back. The external dimensions of the footings are 30 x 30 feet. The excavation is 8 feet deep and you need to add 2 feet on each side to install the footing forms. What is the volume of cubic yards of excavation? - 486.7cy - 13140cy - 858.8cy - 429.4cyarrow_forwardThe Modulus of Elasticity is 30,000,000 for mild carbon steel. In the plastic state, the unit stress is 25000 psi. What is the strain? - 1.45 - 145.0 - 0.00083 - 1450.0arrow_forward
- The building is twenty-five feet by twenty five feet. The side line of the building and two corners along the line have been staked. What is the diagonal distance and the 90 degree distance to the other corners? - 35.36 feet and 35.36 feet - 25.00 feet and 35.36 feet - 35.36 feet and 25 feet - 25.00 feet and 25.00 feetarrow_forwardNEED HELP THANK YOU IN ADVACEarrow_forwardNEED HELP THANK YOU IN ADVANCEarrow_forward
 Fundamentals of Geotechnical Engineering (MindTap...Civil EngineeringISBN:9781305635180Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Fundamentals of Geotechnical Engineering (MindTap...Civil EngineeringISBN:9781305635180Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Principles of Geotechnical Engineering (MindTap C...Civil EngineeringISBN:9781305970939Author:Braja M. Das, Khaled SobhanPublisher:Cengage Learning
Principles of Geotechnical Engineering (MindTap C...Civil EngineeringISBN:9781305970939Author:Braja M. Das, Khaled SobhanPublisher:Cengage Learning Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781305081550Author:Braja M. DasPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781305081550Author:Braja M. DasPublisher:Cengage Learning



