Chapter 16.2, Problem 19E

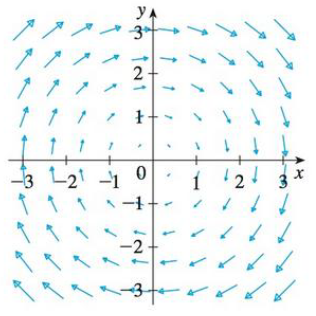
Let F be the vector field shown in the figure.

(a) If C₁ is the vertical line segment from (−3, −3) to (−3, 3), determine whether ${\displaystyle \underset{c_1}{\int }\text{F}\cdot d\text{r}}$ is positive, negative, or zero.

(b) If C₂ is the counterclockwise-oriented circle with radius 3 and center the origin, determine whether ${\displaystyle \underset{c_2}{\int }\text{F}\cdot d\text{r}}$ is positive, negative, or zero.