Calculus, Early Transcendentals
9th Edition
ISBN: 9781337613927
Author: Stewart
Publisher: CENGAGE L
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 16.1, Problem 21E
Match the
21.
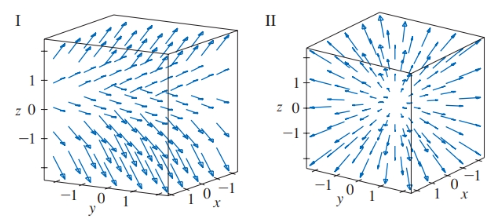
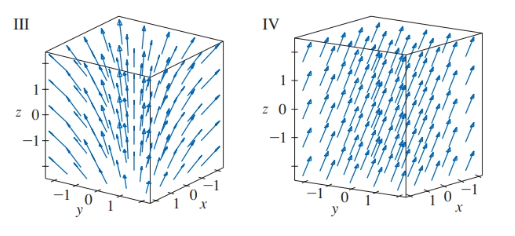
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
(2) (8 points) Determine normal vectors for the planes given by the equations x-y+2z = 3
and 2x + z = 3. Then determine a parametrization of the intersection line of the two
planes.
(3) (6 points)
(a) (4 points) Find all vectors u in the yz-plane that have magnitude [u
also are at a 45° angle with the vector j = (0, 1,0).
= 1 and
(b) (2 points) Using the vector u from part (a) that is counterclockwise to j, find an
equation of the plane through (0,0,0) that has u as its normal.
(1) (4 points) Give a parametrization c: R R³ of the line through the points P =
(1,0,-1) and Q = (-2, 0, 1).
Chapter 16 Solutions
Calculus, Early Transcendentals
Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...
Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Match the vector fields F with the plots labeled...Ch. 16.1 - Match the vector fields F with the plots labeled...Ch. 16.1 - Match the vector fields F with the plots labeled...Ch. 16.1 - Match the vector fields F with the plots labeled...Ch. 16.1 - Match the vector fields F with the plots labeled...Ch. 16.1 - Match the vector fields F with the plots labeled...Ch. 16.1 - Match the vector fields F on 3 with the plots...Ch. 16.1 - Match the vector fields F on 3 with the plots...Ch. 16.1 - Match the vector fields F on 3 with the plots...Ch. 16.1 - Match the vector fields F on 3 with the plots...Ch. 16.1 - Use graphing software to plot the vector field...Ch. 16.1 - Let F(x)=r22rx , where x=x,y and r=x . Use...Ch. 16.1 - Find the gradient vector field of f. 21. f(x, y) =...Ch. 16.1 - Find the gradient vector field of f. 22. f(s, t) =...Ch. 16.1 - Find the gradient vector field of f. 23. f(x, y,...Ch. 16.1 - Find the gradient vector field of f. 24. f(x, y,...Ch. 16.1 - Find the gradient vector field f of f and sketch...Ch. 16.1 - Find the gradient vector field f of f and sketch...Ch. 16.1 - Match the functions f with the plots of their...Ch. 16.1 - Match the functions f with the plots of their...Ch. 16.1 - Match the functions f with the plots of their...Ch. 16.1 - Prob. 34ECh. 16.1 - Prob. 35ECh. 16.1 - Plot the gradient vector field of f together with...Ch. 16.1 - A particle moves in a velocity field V(x, y) = x2,...Ch. 16.1 - At time t = 1, a particle is located at position...Ch. 16.1 - Prob. 39ECh. 16.1 - Prob. 40ECh. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Prob. 8ECh. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Let F be the vector field shown in the figure. (a)...Ch. 16.2 - The figure shows a vector field F and two curves...Ch. 16.2 - Prob. 21ECh. 16.2 - Prob. 22ECh. 16.2 - Evaluate the line integral C F dr, where C is...Ch. 16.2 - Evaluate the line integral C F dr, where C is...Ch. 16.2 - Use a calculator or computer to evaluate the line...Ch. 16.2 - Use a calculator or computer to evaluate the line...Ch. 16.2 - Prob. 34ECh. 16.2 - A thin wire is bent into the shape of a semicircle...Ch. 16.2 - A thin wire has the shape of the first-quadrant...Ch. 16.2 - Prob. 37ECh. 16.2 - Prob. 38ECh. 16.2 - If a wire with linear density (x, y) lies along a...Ch. 16.2 - If a wire with linear density (x, y, z) lies along...Ch. 16.2 - Find the work done by the force field F(x, y) = x...Ch. 16.2 - Find the work done by the force field F(x, y) = x2...Ch. 16.2 - Find the work done by the force field F(x, y, z) =...Ch. 16.2 - The force exerted by an electric charge at the...Ch. 16.2 - The position of an object with mass m at time t is...Ch. 16.2 - Prob. 46ECh. 16.2 - A 160-lb man carries a 25-lb can of paint up a...Ch. 16.2 - Prob. 48ECh. 16.2 - (a) Show that a constant force field does zero...Ch. 16.2 - Prob. 50ECh. 16.2 - Prob. 51ECh. 16.2 - Prob. 52ECh. 16.2 - An object moves along the curve C shown in the...Ch. 16.2 - Experiments show that a steady current I in a long...Ch. 16.3 - The figure shows a curve C and a contour map of a...Ch. 16.3 - A table of values of a function f with continuous...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - The figure shows the vector field F(x, y) = 2xy,...Ch. 16.3 - Prob. 13ECh. 16.3 - Prob. 14ECh. 16.3 - Prob. 15ECh. 16.3 - Prob. 18ECh. 16.3 - (a) Find a function f such that F = f and (b) use...Ch. 16.3 - (a) Find a function f such that F = f and (b) use...Ch. 16.3 - Prob. 23ECh. 16.3 - (a) Find a function f such that F = f and (b) use...Ch. 16.3 - Show that the line integral is independent of path...Ch. 16.3 - Show that the line integral is independent of path...Ch. 16.3 - Suppose youre asked to determine the curve that...Ch. 16.3 - Suppose an experiment determines that the amount...Ch. 16.3 - Find the work done by the force field F in moving...Ch. 16.3 - Find the work done by the force field F in moving...Ch. 16.3 - Is the vector field shown in the figure...Ch. 16.3 - Is the vector field shown in the figure...Ch. 16.3 - Prob. 33ECh. 16.3 - Let F = f, where f(x, y) = sin(x 2y). Find...Ch. 16.3 - Show that if the vector field F = P i + Q j + R k...Ch. 16.3 - Prob. 36ECh. 16.3 - Determine whether or not the given set is (a)...Ch. 16.3 - Determine whether or not the given set is (a)...Ch. 16.3 - Prob. 39ECh. 16.3 - Determine whether or not the given set is (a)...Ch. 16.3 - Let F(x, y) = yi+xjx2+y2 (a) Show that P/y=Q/x....Ch. 16.4 - Evaluate the line integral by two methods: (a)...Ch. 16.4 - Evaluate the line integral by two methods: (a)...Ch. 16.4 - Evaluate the line integral by two methods: (a)...Ch. 16.4 - Evaluate the line integral by two methods: (a)...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Green's Theorem to evaluate the line integral...Ch. 16.4 - Use Green's Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Green's Theorem to evaluate cFdr . (Check the...Ch. 16.4 - Use Green's Theorem to evaluate cFdr . (Check the...Ch. 16.4 - Use Green's Theorem to evaluate CFdr . (Check the...Ch. 16.4 - Use Green's Theorem to evaluate CFdr . (Check the...Ch. 16.4 - Prob. 17ECh. 16.4 - Use Green's Theorem to evaluate CFdr . (Check the...Ch. 16.4 - Prob. 19ECh. 16.4 - Prob. 20ECh. 16.4 - Prob. 21ECh. 16.4 - A particle starts at the origin, moves along the...Ch. 16.4 - Use one of the formulas in (5) to find the area...Ch. 16.4 - Prob. 24ECh. 16.4 - (a) If C is the line segment connecting the point...Ch. 16.4 - Let D be a region bounded by a simple closed path...Ch. 16.4 - Use Exercise 26 to find the centroid of a...Ch. 16.4 - Prob. 28ECh. 16.4 - Prob. 29ECh. 16.4 - Prob. 30ECh. 16.4 - Use the method of Example 5 to calculate C F dr,...Ch. 16.4 - Calculate C F dr, where F(x, y) = x2 + y, 3x y2...Ch. 16.4 - If F is the vector field of Example 5, show that C...Ch. 16.4 - Complete the proof of the special case of Greens...Ch. 16.4 - Use Greens Theorem to prove the change of...Ch. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Prob. 6ECh. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Prob. 9ECh. 16.5 - Prob. 10ECh. 16.5 - Prob. 11ECh. 16.5 - Prob. 12ECh. 16.5 - (a) Verify Formula 3 for f(x,y,z)=sinxyz . (b)...Ch. 16.5 - Let f be a scalar field and F a vector field....Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Is there a vector field G on 3 such that curl G =...Ch. 16.5 - Is there a vector field G on 3 such that curl G =...Ch. 16.5 - Show that any vector field of the form F(x, y, z)...Ch. 16.5 - Show that any vector field of the form F(x, y, z)...Ch. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Prob. 26ECh. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Let r = x i + y j + z k and r = |r|. 30. Verify...Ch. 16.5 - Prob. 33ECh. 16.5 - Let r = x i + y j + z k and r = |r|. 32. If F =...Ch. 16.5 - Use Greens Theorem in the form of Equation 13 to...Ch. 16.5 - Prob. 36ECh. 16.5 - Prob. 37ECh. 16.5 - Use Green's first identity to show that if f is...Ch. 16.5 - Prob. 41ECh. 16.6 - Determine whether the points P and Q lie on the...Ch. 16.6 - Determine whether the points P and Q lie on the...Ch. 16.6 - Identify the surface with the given vector...Ch. 16.6 - Prob. 4ECh. 16.6 - Prob. 5ECh. 16.6 - Prob. 6ECh. 16.6 - Prob. 7ECh. 16.6 - Prob. 9ECh. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Prob. 17ECh. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Prob. 20ECh. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Prob. 27ECh. 16.6 - Prob. 28ECh. 16.6 - Prob. 29ECh. 16.6 - Find parametric equations for the surface obtained...Ch. 16.6 - Prob. 31ECh. 16.6 - Prob. 32ECh. 16.6 - Find an equation of the tangent plane to the given...Ch. 16.6 - Find an equation of the tangent plane to the given...Ch. 16.6 - Find an equation of the tangent plane to the given...Ch. 16.6 - Find an equation of the tangent plane to the given...Ch. 16.6 - Prob. 37ECh. 16.6 - Find an equation of the tangent plane to the given...Ch. 16.6 - Find the area of the surface. 39. The part of the...Ch. 16.6 - Prob. 40ECh. 16.6 - Find the area of the surface. 41. The part of the...Ch. 16.6 - Find the area of the surface. 42. The part of the...Ch. 16.6 - Find the area of the surface. 43. The surface z =...Ch. 16.6 - Find the area of the surface. 44. The part of the...Ch. 16.6 - Find the area of the surface. 45. The part of the...Ch. 16.6 - Prob. 46ECh. 16.6 - Find the area of the surface. 47. The part of the...Ch. 16.6 - Find the area of the surface. 48. The helicoid (or...Ch. 16.6 - Find the area of the surface. 49. The surface with...Ch. 16.6 - Find the area of the surface. 50. The part of the...Ch. 16.6 - Prob. 51ECh. 16.6 - Find the area of the surface correct to four...Ch. 16.6 - Find the area of the surface correct to four...Ch. 16.6 - Prob. 59ECh. 16.6 - (a) Show that the parametric equationsx = acosh u...Ch. 16.6 - Find the area of the part of the spherex2+y2+ z2=...Ch. 16.6 - The figure shows the surface created when the...Ch. 16.6 - Find the area of the part of the spherex2+y2+ z2 =...Ch. 16.7 - LetSbe the surface of the box enclosed by the...Ch. 16.7 - A surface S consists of the cylinderx2+ y2=1, 1 z...Ch. 16.7 - Prob. 3ECh. 16.7 - Suppose thatf(x, y,z)=g(), where g is a function...Ch. 16.7 - Evaluate the surface integral. 6. s xyz dS, Sis...Ch. 16.7 - Evaluate the surface integral. 7. s y dS,Sis the...Ch. 16.7 - Evaluate the surface integral. 8.s (x2+ y2)dS, Sis...Ch. 16.7 - Evaluate the surface integral. 9. s x2yz dS, Sis...Ch. 16.7 - Evaluate the surface integral. 10. s xz dS, S is...Ch. 16.7 - Evaluate the surface integral. 11. s x dS, S is...Ch. 16.7 - Evaluate the surface integral. 12. s y dS, S is...Ch. 16.7 - Evaluate the surface integral. 13. s z2dS, S is...Ch. 16.7 - Evaluate the surface integral. 14. s y2z2 dS, S is...Ch. 16.7 - Evaluate the surface integral. 16 s y2 dS, S is...Ch. 16.7 - Evaluate the surface integral. 17. s (x2z +...Ch. 16.7 - Evaluate the surface integral. 18. s (x + y + z)...Ch. 16.7 - Evaluate the surface integral. 20. s (x2 + y2 +...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - F(x,y,z)=yz, S consists of the paraboloid...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Prob. 29ECh. 16.7 - Prob. 30ECh. 16.7 - Find a formula for s F dS similar to Formula 10...Ch. 16.7 - Find the center of mass of the hemisphere x2 + y2...Ch. 16.7 - Find the mass of a thin funnel in the shape of a...Ch. 16.7 - (a) Give an integral expression for the moment of...Ch. 16.7 - Let S be the part of the sphere x2 + y2 + z2 = 25...Ch. 16.7 - Prob. 43ECh. 16.7 - Prob. 44ECh. 16.7 - Use Gausss Law to find the charge contained in the...Ch. 16.7 - Use Gausss Law to find the charge enclosed by the...Ch. 16.7 - The temperature at the point (x, y, z) in a...Ch. 16.7 - Prob. 48ECh. 16.7 - Let F be an inverse square field, that is, |F(r) =...Ch. 16.8 - Use Stokes Theorem to evaluate s curl F dS. 2....Ch. 16.8 - Use Stokes Theorem to evaluate s curl F dS. 3....Ch. 16.8 - Use Stokes Theorem to evaluate s curl F dS. 4....Ch. 16.8 - F(x, y, z) = xyz i + xy j + x2yz k. S consists of...Ch. 16.8 - F(x,y,z)=exyi+exzj+x2zk S is the half of the...Ch. 16.8 - Use Stokes Theorem to evaluate c F dr. In each...Ch. 16.8 - Use Stokes Theorem to evaluate c F dr. In each...Ch. 16.8 - Use Stokes' Theorem to evaluate CFdr . In each...Ch. 16.8 - Use Stokes Theorem to evaluate c F dr. In each...Ch. 16.8 - F(x,y,z)=yx2,xy2,exy,C is the circle in the...Ch. 16.8 - F(x,y,z)=zexi+zy3j+xz3k C is the circle...Ch. 16.8 - F(x,y,z)=x2yi+x3j+eztan1zk C is the curve with...Ch. 16.8 - F(x,y,z)=x3z,xy,y+z2,C is the curve of...Ch. 16.8 - (a) Use Stokes Theorem to evaluate c F dr, where...Ch. 16.8 - (a) Use Stokes Theorem to evaluate c F dr, where...Ch. 16.8 - Verify that Stokes Theorem is true for the given...Ch. 16.8 - Verify that Stokes Theorem is true for the given...Ch. 16.8 - Verify that Stokes Theorem is true for the given...Ch. 16.8 - Prob. 20ECh. 16.8 - A particle moves along line segments from the...Ch. 16.8 - Evaluate c (y + sin x) dx + (z2 + cos y) dy + x3...Ch. 16.8 - If S is a sphere and F satisfies the hypotheses of...Ch. 16.8 - Suppose S and C satisfy the hypotheses of Stokes...Ch. 16.9 - Verify that the Divergence Theorem is true for the...Ch. 16.9 - Verify that the Divergence Theorem is true for the...Ch. 16.9 - Verify that the Divergence Theorem is true for the...Ch. 16.9 - Verify that the Divergence Theorem is true for the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Prob. 13ECh. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Prob. 16ECh. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to evaluate s F dS,...Ch. 16.9 - Let F(x, y, z) = z tan-1(y2) i + z3 ln(x2 + 1) j +...Ch. 16.9 - Prob. 21ECh. 16.9 - (a) Are the points P1 and P2 sources or sinks for...Ch. 16.9 - Prob. 23ECh. 16.9 - Prob. 24ECh. 16.9 - Verify that div E = 0 for the electric field...Ch. 16.9 - Prob. 26ECh. 16.9 - Prove each identity, assuming that S and E satisfy...Ch. 16.9 - Prob. 28ECh. 16.9 - Prob. 29ECh. 16.9 - Prove each identity, assuming that S and E satisfy...Ch. 16.9 - Prob. 31ECh. 16.9 - Prove each identity, assuming that S and E satisfy...Ch. 16.9 - Prob. 33ECh. 16.9 - Prob. 34ECh. 16 - What is a vector field? Give three examples that...Ch. 16 - Prob. 2CCCh. 16 - Prob. 3CCCh. 16 - (a) Define the line integral of a vector field F...Ch. 16 - Prob. 5CCCh. 16 - Prob. 6CCCh. 16 - Prob. 7CCCh. 16 - Write expressions for the area enclosed by a curve...Ch. 16 - Prob. 9CCCh. 16 - Prob. 10CCCh. 16 - Prob. 11CCCh. 16 - Prob. 12CCCh. 16 - Prob. 13CCCh. 16 - Prob. 14CCCh. 16 - Prob. 15CCCh. 16 - Prob. 16CCCh. 16 - Determine whether the statement is true or false....Ch. 16 - Prob. 2TFQCh. 16 - Prob. 3TFQCh. 16 - Prob. 4TFQCh. 16 - Prob. 5TFQCh. 16 - Prob. 6TFQCh. 16 - Determine whether the statement is true or false....Ch. 16 - Prob. 8TFQCh. 16 - Determine whether the statement is true or false....Ch. 16 - Prob. 10TFQCh. 16 - Prob. 11TFQCh. 16 - Prob. 12TFQCh. 16 - Determine whether the statement is true or false....Ch. 16 - A vector field F, a curve C, and a point P are...Ch. 16 - Evaluate the line integral. 2. C x ds, C is the...Ch. 16 - Evaluate the line integral. 3. C yz cos x ds, C: x...Ch. 16 - Evaluate the line integral. 4. C y dx + (x + y2)...Ch. 16 - Evaluate the line integral. 5. C y3 dx + x2 dy, C...Ch. 16 - Evaluate the line integral. 6. C xy dx + ey dy +...Ch. 16 - Evaluate the line integral. 7. C xy dx + y2 dy +...Ch. 16 - Evaluate the line integral. 8. C F dr, where F(x,...Ch. 16 - Evaluate the line integral. 9. C F dr, where...Ch. 16 - Find the work done by the force field F(x, y, z) =...Ch. 16 - Show that F is a conservative vector field. Then...Ch. 16 - Show that F is a conservative vector field. Then...Ch. 16 - Show that F is a conservative and use this fact to...Ch. 16 - Show that F is a conservative and use this fact to...Ch. 16 - Verify that Greens Theorem is true for the line...Ch. 16 - Use Greens Theorem to evaluate C 1+x3dx + 2xydy...Ch. 16 - Prob. 17ECh. 16 - Find curl F and div F if F(x, y, z) = e-x sin y i...Ch. 16 - Show that there is no vector field G such that...Ch. 16 - If F and G are vector fields whose component...Ch. 16 - If C is any piecewise-smooth simple closed plane...Ch. 16 - If f and g are twice differentiable functions,...Ch. 16 - If f is a harmonic function, that is, 2f = 0, show...Ch. 16 - Prob. 24ECh. 16 - Find the area of the part of the surface z = x2 +...Ch. 16 - (a) Find an equation of the tangent plane at the...Ch. 16 - Evaluate the surface integral. 27. S z dS, where S...Ch. 16 - Evaluate the surface integral. 28. s (x2z +...Ch. 16 - Evaluate the surface integral. 29. S F dS, where...Ch. 16 - Evaluate the surface integral. 30. S F dS, where...Ch. 16 - Verify that Stokes Theorem is true for the vector...Ch. 16 - Use Stokes Theorem to evaluate s curl F dS, where...Ch. 16 - Use Stokes Theorem to evaluate C F dr, where F(x,...Ch. 16 - Use the Divergence Theorem to calculate the...Ch. 16 - Verify that the Divergence Theorem is true for the...Ch. 16 - Compute the outward flux of F(x, y, z) =...Ch. 16 - Let F(x, y, z) = (3x2 yz 3y) i + (x3z 3x) j +...Ch. 16 - Prob. 38ECh. 16 - Prob. 39ECh. 16 - If the components of F have continuous second...Ch. 16 - Prob. 41ECh. 16 - 1. Let S be a smooth parametric surface and let P...Ch. 16 - Find the positively oriented simple closed curve C...Ch. 16 - Let C be a simple closed piecewise-smooth space...Ch. 16 - Prove the following identity: (F G) = (F )G + (G...Ch. 16 - Prob. 6PP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 4. Consider the initial value problem y' = 3x(y-1) 1/3, y(xo) = yo. (a) For what points (co, yo) does the IVP have a solution? (b) For what points (xo, yo) does the IVP have a unique solution on some open interval that contains 20? (c) Solve the IVP y' = 3x(y-1) 1/3, y(0) = 9 and determine the largest open interval on which this solution is unique.arrow_forwardFind the limit. (If the limit is infinite, enter 'oo' or '-o', as appropriate. If the limit does not otherwise exist, enter DNE.) lim X→ ∞ (✓ 81x2 - 81x + x 9x)arrow_forward2) Compute the following anti-derivative. √1x4 dxarrow_forward
- Question 3 (5pt): A chemical reaction. In an elementary chemical reaction, single molecules of two reactants A and B form a molecule of the product C : ABC. The law of mass action states that the rate of reaction is proportional to the product of the concentrations of A and B: d[C] dt = k[A][B] (where k is a constant positive number). Thus, if the initial concentrations are [A] = = a moles/L and [B] = b moles/L we write x = [C], then we have (E): dx dt = k(ax)(b-x) 1 (a) Write the differential equation (E) with separate variables, i.e. of the form f(x)dx = g(t)dt. (b) Assume first that a b. Show that 1 1 1 1 = (a - x) (b - x) - a) a - x b - x b) (c) Find an antiderivative for the function f(x) = (a-x) (b-x) using the previous question. (d) Solve the differentiel equation (E), i.e. find x as a function of t. Use the fact that the initial concentration of C is 0. (e) Now assume that a = b. Find x(t) assuming that a = b. How does this expression for x(t) simplify if it is known that [C] =…arrow_forward3) Find the volume of the solid that lies inside both the sphere x² + y² + z² cylinder x²+y² = 1. = 4 and thearrow_forward1) Compute the following limit. lim x-0 2 cos(x) 2x² - x4arrow_forward
- y = f(x) b C The graph of y = f(x) is shown in the figure above. On which of the following intervals are dy > 0 and dx d²y dx2 <0? I. aarrow_forward3 2 1 y O a The graph of the function f is shown in the figure above. Which of the following statements about f is true? о limb f(x) = 2 Olima f(x) = 2 о lima f (x) = lim x →b f(x) → f (x) = 1 limb. lima f(x) does not existarrow_forwardQuestion 1 (1pt). The graph below shows the velocity (in m/s) of an electric autonomous vehicle moving along a straight track. At t = 0 the vehicle is at the charging station. 1 8 10 12 0 2 4 6 (a) How far is the vehicle from the charging station when t = 2, 4, 6, 8, 10, 12? (b) At what times is the vehicle farthest from the charging station? (c) What is the total distance traveled by the vehicle?arrow_forwardQuestion 2 (1pt). Evaluate the following (definite and indefinite) integrals (a) / (e² + ½) dx (b) S (3u 2)(u+1)du (c) [ cos³ (9) sin(9)do .3 (d) L³ (₂ + 1 dzarrow_forward= Question 4 (5pt): The Orchard Problem. Below is the graph y f(t) of the annual harvest (assumed continuous) in kg/year from my cranapple orchard t years after planting. The trees take about 25 years to get established, and from that point on, for the next 25 years, they give a fairly good yield. But after 50 years, age and disease are taking their toll, and the annual yield is falling off. 40 35 30 。 ៣៩ ថា8 8 8 8 6 25 20 15 10 y 5 0 0 5 10 15 20 25 30 35 40 45 50 55 60 The orchard problem is this: when should the orchard be cut down and re- planted, thus starting the cycle again? What you want to do is to maximize your average harvest per year over a full cycle. Of course there are costs to cutting the orchard down and replanting, but it turns out that we can ignore these. The first cost is the time it takes to cut the trees down and replant but we assume that this can effectively be done in a week, and the loss of time is negligible. Secondly there is the cost of the labour to cut…arrow_forwardnd ave a ction and ave an 48. The domain of f y=f'(x) x 1 2 (= x<0 x<0 = f(x) possible. Group Activity In Exercises 49 and 50, do the following. (a) Find the absolute extrema of f and where they occur. (b) Find any points of inflection. (c) Sketch a possible graph of f. 49. f is continuous on [0,3] and satisfies the following. X 0 1 2 3 f 0 2 0 -2 f' 3 0 does not exist -3 f" 0 -1 does not exist 0 ve tes where X 0 < x <1 1< x <2 2arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_iosRecommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:CengageElementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage LearningLinear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Basic Differentiation Rules For Derivatives; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=IvLpN1G1Ncg;License: Standard YouTube License, CC-BY