
Concept explainers
(a)
The depth of cut for the given piece of round stock.
Answer to Problem 35A
Depth of cut for the given piece of round stock should be
Explanation of Solution
Given information:
The formula for calculating the depth of round stock piece is given by -
Where,

Also, given that -
Calculation:
As per the problem statement, the formula for calculating the depth of round stock piece is given by -
Here, we have been given
Putting above values in given formula for depth of cut and following order of operation as below.
Hence, depth of cut for the given piece of round stock should be
(b)
To evaluate required depth of cut for the given piece of round stock.
Answer to Problem 35A
Depth of cut for the given piece of round stock should be
Explanation of Solution
Given information:
The formula for calculating the depth of round stock piece is given by -
Where,
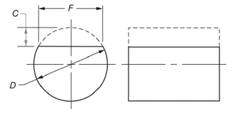
Also, given that -
Calculation:
As per the problem statement, the formula for calculating the depth of round stock piece is given by -
Here, we have been given
Putting above values in given formula for depth of cut and following order of operation as below.
Hence, depth of cut for the given piece of round stock should be
(c)
To find out the required depth of cut for the given piece of round stock.
Answer to Problem 35A
Depth of cut for the given piece of round stock should be
Explanation of Solution
Given information:
The formula for calculating the depth of round stock piece is given by -
Where,
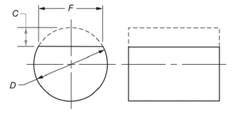
Also, given that -
Calculation:
As per the problem statement, the formula for calculating the depth of round stock piece is given by -
Here, we have been given
Putting above values in given formula for depth of cut and following order of operation as below.
Hence, depth of cut for the given piece of round stock should be
Want to see more full solutions like this?
Chapter 16 Solutions
EBK MATHEMATICS FOR MACHINE TECHNOLOGY
- Problems Construct shear and moment diagrams using the equilib- rium method. Indicate the magnitudes of Vmax and Mmax. 7.4 8=2K/FT. W=2K/FT. 10' 10'arrow_forwardProblems Determine I, and Iy for the cross-sections 6.8 89 2" 1011 2" ส 10 |x= ly=arrow_forwardProblems Construct shear and moment diagrams using the equilib- rium method. Indicate the magnitudes of Vmax and Mmax. 7.3 107 B 5' 201arrow_forward
- Can you help me with this problem using linear recurrance: Find an explicit formula for the recurrence relation an = 2can−1 + 3c2an−2 where c not equal to 0 with initial conditions a0=4c and a1 = 0arrow_forwardCan you help me solved this problem using generalized combination:How many combinations are there to pick r objects from 2n objects numbered from 1to 2n when repetitions are allowed and at least one object of odd type does not appear?arrow_forwardNarrow_forward
- Please help me organize the proof of the following theorem:arrow_forwardHow come that I marked ?arrow_forwardIn Exercises 1-14, state whether each statement is true or false. If false, give a reason. 1. The set of stores located in the state of Wyoming is a well- defined set. 2. The set of the three best songs is a well-defined set. 3. maple = {oak, elm, maple, sycamore} 4{} cơ 5. {3, 6, 9, 12,...} and {2, 4, 6, 8, ...} are disjoint sets. 6. {Mercury, Venus, Earth, Mars} is an example of a set in roster form. 7. {candle, picture, lamp} = {picture, chair, lamp } 8. {apple, orange, banana, pear} is equivalent to {tomato, corn, spinach, radish}.arrow_forward
- Exercises Evaluate the following limits. 1. lim cot x/ln x +01x 2. lim x² In x +014 3. lim x* x0+ 4. lim (cos√√x)1/x +014 5. lim x2/(1-cos x) x10 6. lim e*/* 818 7. lim (secx - tan x) x-x/2- 8. lim [1+(3/x)]* x→∞0arrow_forwardIn Exercises 1 through 3, let xo = O and calculate P7(x) and R7(x). 1. f(x)=sin x, x in R. 2. f(x) = cos x, x in R. 3. f(x) = In(1+x), x≥0. 4. In Exercises 1, 2, and 3, for |x| 1, calculate a value of n such that P(x) approximates f(x) to within 10-6. 5. Let (an)neN be a sequence of positive real numbers such that L = lim (an+1/an) exists in R. If L < 1, show that an → 0. [Hint: Let 1111 Larrow_forwardiation 7. Let f be continuous on [a, b] and differentiable on (a, b). If lim f'(x) xia exists in R, show that f is differentiable at a and f'(a) = lim f'(x). A similar result holds for b. x-a 8. In reference to Corollary 5.4, give an example of a uniformly continuous function on [0, 1] that is differentiable on (0, 1] but whose derivative is not bounded there. 9. Recall that a fixed point of a function f is a point c such that f(c) = c. (a) Show that if f is differentiable on R and f'(x)| x if x 1 and hence In(1+x) 0. 12. For 0 л/2. (Thus, as x л/2 from the left, cos x is never large enough for x+cosx to be greater than л/2 and cot x is never small enough for x + cot x to be less than x/2.)arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal LittellAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal LittellAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,





