
Concept explainers
(a)
Interpretation:
The length of the face diagonal in terms of
Concept introduction:
The crystal can exist in various shapes but the most common one is cubic. The FCC unit cell has lattice points at eight corners of the unit cell along with the face centers of unit cell. The total number of atoms in FCC unit cell is four.
Answer to Problem 1ASA
The length of the face diagonal in terms of
Explanation of Solution
The face diagonal BC, represented by a, is shown below.

Figure 1
In the Figure 1, the face diagonal, represented by a, is the hypotenuse of right angle triangle ABC. The given unit cell is cube. Therefore, the length of AB will be equal to length of AC.
Therefore,
The length of face diagonal is calculated by using Pythagoras theorem as shown below.
Substitute the value of AB and AC in equation (1)
Therefore, the length of the face diagonal in terms of
The length of the face diagonal in terms of
(b)
Interpretation:
The length of the cube diagonal in terms of
Concept introduction:
The crystal can exist in various shapes but the most common one is cubic. The FCC unit cell has lattice points at eight corners of the unit cell along with the face centers of unit cell. The total number of atoms in FCC unit cell is four.
Answer to Problem 1ASA
The length of the cube diagonal in terms of
Explanation of Solution
A line that runs from one corner to other corner of the cube via centre of the cube is termed as cube diagonal. The cube diagonal is represented by CE as shown below.
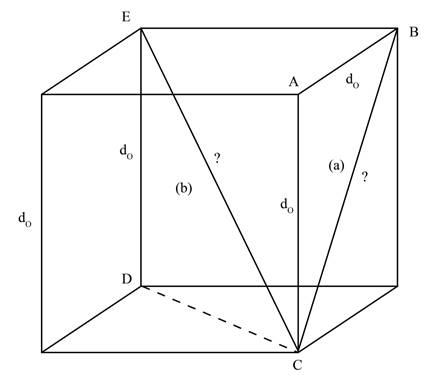
Figure 2
In the Figure 2, the cube diagonal, represented by b, is the hypotenuse of right angle triangle CDE. The edge length DE is given as
Therefore,
The length of face diagonal is calculated by using Pythagoras theorem as shown below.
Substitute the value of edge length DE and face diagonal CD in equation (2).
Therefore, the length of the cube diagonal in terms of
The length of the cube diagonal in terms of
Want to see more full solutions like this?
Chapter 16 Solutions
Chemical Principles in the Laboratory
- File Preview The following is a total synthesis of the pheromone of the western pine beetle. Such syntheses are interesting both because of the organic chemistry, and because of the possibility of using species specific insecticides, rather than broad band insecticides. Provide the reagents for each step. There is some chemistry from our most recent chapter in this synthesis, but other steps are review from earlier chapters. (8 points) COOEt COOEt A C COOEt COOEt COOH B OH OTS CN D E See the last homework set F for assistance on this one. H+, H₂O G OH OH The last step is just nucleophilic addition reactions, taking the ketone to an acetal, intramolecularly. But it is hard to visualize the three dimensional shape as it occurs. Frontalin, pheromone of the western pine beetlearrow_forwardFor the reaction below: 1. Draw all reasonable elimination products to the right of the arrow. 2. In the box below the reaction, redraw any product you expect to be a major product. C Major Product: Check + ◎ + X ง © Cl I F2 80 F3 I σ F4 I F5 NaOH Click and drawing F6 A 2025 McGraw Hill LLC. All Rights E F7 F8 $ # % & 2 3 4 5 6 7 8 Q W E R T Y U A S D F G H Jarrow_forwardCan I please get help with this graph. If you can show exactly where it needs to pass through.arrow_forward
- N Draw the major product of this reaction. Ignore inorganic byproducts. D 1. H₂O, pyridine 2. neutralizing work-up V P W X DE CO e C Larrow_forwardDraw the major product of this reaction. Ignore inorganic byproducts. N O' 1. H2O, pyridine 2. neutralizing work-up く 8 W aarrow_forwardIdeal Gas Law Practice Name If you need a refresher on Ideal Gas Law, go back to your Ideal Gas Law Reading Assignment from last week! On all of the following, you'll need to make sure to convert pressures to atm and convert temperatures to Kelvin in order to be able to use the R gas constant on your equation sheet! Given: Ideal Gas Law = then P= pressure V = volume R= ideal gas consent PV=nRT namount of substance n=PV/TR P=nRT/V I = temperature V=nRT/P T=PV/nR R=PV/nT 1. What pressure is required to contain 0.023 moles of nitrogen gas in a 4.2 L container at a temperature of 20.°C? 2. Oxygen gas is collected at a pressure of 123 kPa in a container which has a volume of 10.0 L. What temperature must be maintained on 0.500 moles of this gas in order to maintain this pressure? Express the temperature in degrees Celsius. 3. How many moles of chlorine gas would occupy a volume of 35.5 L at a pressure of 100.0 kPa and a temperature of 100. °C? After determining the number of moles,…arrow_forward
- 1. The following conversion includes chemistry we have covered very recently, some chemistry from last term, and chemistry from the first chapter of this unit. Provide curly arrows and an explanation for this mechanism. Use the reagents in the order given. You do not need any other reagents. 1. NaOEt OEt 2.arrow_forwardCOOEt COOEt Step 1 Step 2 Step 3 COOEt COOEt COOH Step 6 OH Step 4 Step 7 (racemic) cyclizes under conditions (8) OTS Step 5 Step 8 ОН OH (racemic) Frontalin (racemic) Shown above are the steps in one of the several published syntheses of Frontalin, a pheromone of the western pine beetle. From the choices provided, show the reagents and conditions by which step 3 of this synthesis might be accomplished. List the reagent(s) in order that will accomplish this transformation. No more than 4 steps are required. List your answer as a single letter (single-step transformation) or a series of letters (multi-step transformation) with no commas separating them. For example, "ab" corresponds to: 1. Eto Na+ 2. NaOH, H₂O NOTE: The order in which you list your letters matters! Reagents: a. Eto Na* g. NaCN b. NaOH, H₂O h. SOCI₂ c. H3O+, heat i. (CH3)2CuLi, ether, -78°C d. LiAlH4 j. H₂O e. p-TsCI, pyridine k. RCO3H f. Br I. H3O+ 1,024arrow_forwardK ← nationa Login - Paymentivet MapQue Draw the major product of this reaction. Ignore inorganic byproducts and the carboxylic acid side product. N 1. excess LiAlH4 2. H₂O ✓ W aarrow_forward
- Draw the major product of this reaction. Ignore inorganic byproducts and the alcohol side product. 1. H3O+, heat 2. Neutralizing work-up Drawing Qarrow_forwardIndicate the procedure (reagent Z) to go from compound A1 to compound A2. A1 Z P(C6H5)3 A2arrow_forwardPlease help with this graph.arrow_forward
 Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning
General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning
Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning Chemistry by OpenStax (2015-05-04)ChemistryISBN:9781938168390Author:Klaus Theopold, Richard H Langley, Paul Flowers, William R. Robinson, Mark BlaserPublisher:OpenStax
Chemistry by OpenStax (2015-05-04)ChemistryISBN:9781938168390Author:Klaus Theopold, Richard H Langley, Paul Flowers, William R. Robinson, Mark BlaserPublisher:OpenStax





