Chapter 16, Problem 16.1P

To determine

The structure stiffness matrix for the frame.

Answer to Problem 16.1P

The structure stiffness matrix for the frame is shown below.

   $k=\left[\begin{array}{ccccccccc}4833.33& 0& 0& -4833.33& 0& 0& 0& 0& 0\\ 0& 130.9& 7854.17& 0& -130.9& 7854.17& 0& 0& 0\\ 0& 7854.17& 628333.3& 0& -7854.17& 314166.67& 0& 0& 0\\ -4833.33& 0& 0& 4909.01& 0& 5454.28& -75.754& 0& 5454.28\\ 0& -130.9& -7854.17& 0& 4338.69& -7854.17& 0& 4207.78& 0\\ 0& 7854.17& 314166.67& 5454.28& -7854.17& 11519144.41& 5454.28& 0& 261805.56\\ 0& 0& 0& -75.754& 0& -5454.28& 75.754& 0& -5454.28\\ 0& 0& 0& 0& -4207.78& 0& 0& 4207.78& 0\\ 0& 0& 0& 5454.28& 0& 261805.56& -5454.28& 0& 523611.11\end{array}\right]$

Explanation of Solution

Concept Used:

Write the expression for direction cosine in x-direction.

${\lambda }_x=\frac{x_F-x_N}{L}$          ...... (I)

Here, coordinate of x at near end of the member is $x_F$ and coordinate of x at far end of the member is $x_N$.

Write the expression for direction cosine in x-direction.

${\lambda }_y=\frac{y_F-y_N}{L}$          ...... (II)

Here, coordinate of y at near end of the member is $y_F$ and coordinate of y at far end of the member is $y_N$.

Write the global stiffness matrix for the member.

Here, cross-sectional area of the member is $A$, length of the member is $L$, modulus of elasticity is $E$ and moment of inertia is $I$

Calculation:

The free body diagram of the frame is shown below.

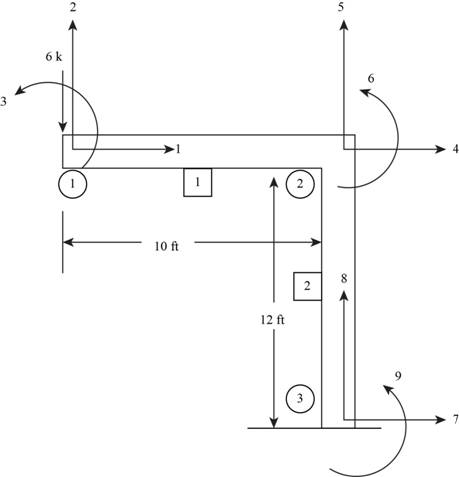
          Figure (1)

Consider the member-1.

Calculate direction cosine in x-direction.

Substitute $10\text{ ft}$ for $x_F$, $0\text{ ft}$ for $x_N$ and $10\text{ ft}$ for $L$ in Equation (I).

$\begin{array}{c}{\lambda }_x=\frac{10\text{ ft}-0\text{ ft}}{10\text{ ft}}\\ =1\end{array}$

Calculate direction cosine in y-direction.

Substitute $0\text{ ft}$ for $y_F$, $0\text{ ft}$ for $y_N$ and $10\text{ ft}$ for $L$ in Equation (II).

$\begin{array}{c}{\lambda }_y=\frac{0\text{ ft}-0\text{ ft}}{10\text{ ft}}\\ =0\end{array}$

The stiffness matrix for member-1 is shown below.

Substitute $1$ for ${\lambda }_x$ and $0$ for ${\lambda }_y$ in global stiffness matrix.

$k_1=\left[\begin{array}{cccccc}\frac{AE}{L}& 0& 0& -\frac{AE}{L}& 0& 0\\ 0& \frac{12EI}{L^3}& \frac{6EI}{L^2}& 0& -\frac{12EI}{L^3}& \frac{6EI}{L^2}\\ 0& \frac{6EI}{L^2}& \frac{4EI}{L}& 0& -\frac{6EI}{L^2}& \frac{2EI}{L}\\ -\frac{AE}{L}& 0& 0& \frac{AE}{L}& 0& 0\\ 0& \frac{12EI}{L^3}& -\frac{6EI}{L^2}& 0& \frac{12EI}{L^3}& -\frac{6EI}{L^2}\\ 0& \frac{6EI}{L^2}& \frac{2EI}{L}& 0& -\frac{6EI}{L^2}& \frac{4EI}{L}\end{array}\right]$          ...... (III)

Calculate the value of $\frac{AE}{L}$ in stiffness matrix.

Substitute $20{\text{ in}}^2$ for $A$, $29\times {10}^3\text{ ksi}$ for $E$ and $10\text{ ft}$ for $L$.

$\begin{array}{c}\frac{AE}{L}=\frac{\left(20{\text{ in}}^2\right)\times \left(29\times {10}^3\text{ ksi}\right)}{\left(10\times 12\right)\text{in}}\\ =4833.33\text{ kips/in}\end{array}$

Calculate the value of $\frac{6EI}{L^2}$ in stiffness matrix.

Substitute $29\times {10}^3\text{ ksi}$ for $E$, $650{\text{ in}}^4$ for $I$ and $10\text{ ft}$ for $L$.

$\begin{array}{c}\frac{6EI}{L^2}=\frac{6\times \left(29\times {10}^3\text{ ksi}\right)\times \left(650{\text{ in}}^4\right)}{{\left(10\times 12\right)}^2{\text{in}}^2}\\ =7854.17\text{ kips}\end{array}$

Calculate the value of $\frac{12EI}{L^3}$ in stiffness matrix.

Substitute $29\times {10}^3\text{ ksi}$ for $E$, $650{\text{ in}}^4$ for $I$ and $10\text{ ft}$ for $L$.

$\begin{array}{c}\frac{12EI}{L^3}=\frac{12\times \left(29\times {10}^3\text{ ksi}\right)\times \left(650{\text{ in}}^4\right)}{{\left(10\times 12\right)}^3{\text{in}}^3}\\ =130.9\text{ kips/in}\end{array}$

Calculate the value of $\frac{4EI}{L}$ in stiffness matrix.

Substitute $29\times {10}^3\text{ ksi}$ for $E$, $650{\text{ in}}^4$ for $I$ and $10\text{ ft}$ for $L$.

$\begin{array}{c}\frac{4EI}{L}=\frac{4\times \left(29\times {10}^3\text{ ksi}\right)\times \left(650{\text{ in}}^4\right)}{\left(10\times 12\right)\text{in}}\\ =628333.3\text{ kip-in}\end{array}$

Calculate the value of $\frac{2EI}{L}$ in stiffness matrix.

Substitute $29\times {10}^3\text{ ksi}$ for $E$, $650{\text{ in}}^4$ for $I$ and $10\text{ ft}$ for $L$.

$\begin{array}{c}\frac{2EI}{L}=\frac{2\times \left(29\times {10}^3\text{ ksi}\right)\times \left(650{\text{ in}}^4\right)}{\left(10\times 12\right)\text{in}}\\ =314166.67\text{ kip-in}\end{array}$

Substitute $4833.33\text{ kips/in}$ for $\frac{AE}{L}$, $7854.17\text{ kips}$ for $\frac{6EI}{L^2}$, $130.9\text{ kips/in}$ for $\frac{12EI}{L^3}$, $628333.3\text{ kip-in}$ for $\frac{4EI}{L}$ and $314166.67\text{ kip-in}$ for $\frac{2EI}{L}$ in matrix (III). $k_1=\left[\begin{array}{cccccc}4833.33& 0& 0& -4833.33& 0& 0\\ 0& 130.9& 7854.17& 0& 130.9& 7854.17\\ 0& 7854.17& 628333.3& 628333.3& -7854.17& 314166.67\\ -4833.33& 0& 0& 4833.33& 0& 0\\ 0& 130.9& -7854.17& 0& 130.9& -7854.17\\ 0& 7854.17& 314166.67& 314166.67& -7854.17& 628333.3\end{array}\right]$          ...... (IV)

Consider the member-2.

Calculate direction cosine in x-direction.

Substitute $0\text{ ft}$ for $x_F$, $0\text{ ft}$ for $x_N$ and $12\text{ ft}$ for $L$ in Equation (I)

$\begin{array}{c}{\lambda }_x=\frac{0\text{ft}-0\text{ft}}{12\text{ft}}\\ =0\end{array}$

Calculate direction cosine in y-direction.

Substitute $0\text{ ft}$ for $y_F$, $-12\text{ ft}$ for $y_N$ and $12\text{ ft}$ for $L$ in Equation (II)

$\begin{array}{c}{\lambda }_y=\frac{0\text{ft}-\left(-12\text{ft}\right)}{12\text{ft}}\\ =1\end{array}$

The stiffness matrix for member-1 is shown below.

Substitute $0$ for ${\lambda }_x$ and $1$ for ${\lambda }_y$ in global stiffness matrix.

   $k_2=\left[\begin{array}{cccccc}\frac{12EI}{L^3}& 0& \frac{6EI}{L^2}& -\frac{12EI}{L^3}& 0& \frac{6EI}{L^2}\\ 0& \frac{AE}{L}& 0& 0& -\frac{AE}{L}& 0\\ \frac{6EI}{L^2}& 0& \frac{4EI}{L}& -\frac{6EI}{L^2}& 0& \frac{2EI}{L}\\ -\frac{12EI}{L^3}& 0& -\frac{6EI}{L^2}& \frac{12EI}{L^3}& 0& -\frac{6EI}{L^2}\\ 0& -\frac{AE}{L}& 0& 0& \frac{AE}{L}& 0\\ \frac{6EI}{L^2}& 0& \frac{2EI}{L}& -\frac{6EI}{L^2}& 0& \frac{4EI}{L}\end{array}\right]$          ...... (V)

Calculate the value of $\frac{AE}{L}$ in stiffness matrix.

Substitute $20{\text{ in}}^2$ for $A$, $29\times {10}^3\text{ ksi}$ for $E$ and $12\text{ ft}$ for $L$.

$\begin{array}{c}\frac{AE}{L}=\frac{\left(20{\text{ in}}^2\right)\times \left(29\times {10}^3\text{ ksi}\right)}{\left(12\times 12\right)\text{in}}\\ =4027.78\text{ kips/in}\end{array}$

Calculate the value of $\frac{6EI}{L^2}$ in stiffness matrix.

Substitute $29\times {10}^3\text{ ksi}$ for $E$, $650{\text{ in}}^4$ for $I$ and $12\text{ ft}$ for $L$.

$\begin{array}{c}\frac{6EI}{L^2}=\frac{6\times \left(29\times {10}^3\text{ ksi}\right)\times \left(650{\text{ in}}^4\right)}{{\left(12\times 12\right)}^2{\text{in}}^2}\\ =5454.28\text{ kips}\end{array}$

Calculate the value of $\frac{12EI}{L^3}$ in stiffness matrix.

Substitute $29\times {10}^3\text{ ksi}$ for $E$, $650{\text{ in}}^4$ for $I$ and $12\text{ ft}$ for $L$.

$\begin{array}{c}\frac{12EI}{L^3}=\frac{12\times \left(29\times {10}^3\text{ ksi}\right)\times \left(650{\text{ in}}^4\right)}{{\left(12\times 12\right)}^3{\text{in}}^3}\\ =75.754\text{ kips/in}\end{array}$

Calculate the value of $\frac{4EI}{L}$ in stiffness matrix.

Substitute $29\times {10}^3\text{ ksi}$ for $E$, $650{\text{ in}}^4$ for $I$ and $12\text{ ft}$ for $L$.

$\begin{array}{c}\frac{4EI}{L}=\frac{4\times \left(29\times {10}^3\text{ ksi}\right)\times \left(650{\text{ in}}^4\right)}{\left(12\times 12\right)\text{in}}\\ =523611.11\text{ kip-in}\end{array}$

Calculate the value of $\frac{2EI}{L}$ in stiffness matrix.

Substitute $29\times {10}^3\text{ ksi}$ for $E$, $650{\text{ in}}^4$ for $I$ and $12\text{ ft}$ for $L$.

$\begin{array}{c}\frac{2EI}{L}=\frac{2\times \left(29\times {10}^3\text{ ksi}\right)\times \left(650{\text{ in}}^4\right)}{\left(12\times 12\right)\text{in}}\\ =261805.56\text{ kip-in}\end{array}$

Substitute $4027.78\text{ kips/in}$ for $\frac{AE}{L}$, $5454.28\text{ kips}$ for $\frac{6EI}{L^2}$, $75.754\text{ kips/in}$ for $\frac{12EI}{L^3}$, $523611.11\text{ kip-in}$ for $\frac{4EI}{L}$ and $261805.56\text{ kip-in}$ for $\frac{2EI}{L}$ in matrix (III).

   $k_2=\left[\begin{array}{cccccc}75.754& 0& 5454.28& -75.754& 0& 5454.28\\ 0& 4027.78& 0& 0& -4027.78& 0\\ 5454.28& 0& 523611.11& -5454.28& 0& 261805.56\\ -75.754& 0& -5454.28& 75.754& 0& -5454.28\\ 0& -4027.78& 0& 0& 4027.78& 0\\ 5454.28& 0& 261805.56& -5454.28& 0& 523611.11\end{array}\right]$          ...... (VI)

The final matrix of the frame by assembling matrices (III) and (IV) is shown below.

   $k=\left[\begin{array}{ccccccccc}4833.33& 0& 0& -4833.33& 0& 0& 0& 0& 0\\ 0& 130.9& 7854.17& 0& -130.9& 7854.17& 0& 0& 0\\ 0& 7854.17& 628333.3& 0& -7854.17& 314166.67& 0& 0& 0\\ -4833.33& 0& 0& 4909.01& 0& 5454.28& -75.754& 0& 5454.28\\ 0& -130.9& -7854.17& 0& 4338.69& -7854.17& 0& 4207.78& 0\\ 0& 7854.17& 314166.67& 5454.28& -7854.17& 11519144.41& 5454.28& 0& 261805.56\\ 0& 0& 0& -75.754& 0& -5454.28& 75.754& 0& -5454.28\\ 0& 0& 0& 0& -4207.78& 0& 0& 4207.78& 0\\ 0& 0& 0& 5454.28& 0& 261805.56& -5454.28& 0& 523611.11\end{array}\right]$

Conclusion:

The structure stiffness matrix for the frame is shown below.

   $k=\left[\begin{array}{ccccccccc}4833.33& 0& 0& -4833.33& 0& 0& 0& 0& 0\\ 0& 130.9& 7854.17& 0& -130.9& 7854.17& 0& 0& 0\\ 0& 7854.17& 628333.3& 0& -7854.17& 314166.67& 0& 0& 0\\ -4833.33& 0& 0& 4909.01& 0& 5454.28& -75.754& 0& 5454.28\\ 0& -130.9& -7854.17& 0& 4338.69& -7854.17& 0& 4207.78& 0\\ 0& 7854.17& 314166.67& 5454.28& -7854.17& 11519144.41& 5454.28& 0& 261805.56\\ 0& 0& 0& -75.754& 0& -5454.28& 75.754& 0& -5454.28\\ 0& 0& 0& 0& -4207.78& 0& 0& 4207.78& 0\\ 0& 0& 0& 5454.28& 0& 261805.56& -5454.28& 0& 523611.11\end{array}\right]$