
(a)
The linear programming problem to maximize the profit if the factors are given as below,
| Resource | Regular | Premium | Supreme | Resource Availability |
| Raw gas | ||||
| Production time | ||||
| Storage | ||||
| Profit |
(a)
Answer to Problem 2P
Solution:
The linear programming problem to maximize the profit is,
Subject to the constraints:
Explanation of Solution
Given Information:
The factors are given as below,
| Resource | Regular | Premium | Supreme | Resource Availability |
| Raw gas | ||||
| Production time | ||||
| Storage | ||||
| Profit |
Assume x be the amount of regular resource, y be the amount of premium resource and z be the amount of supreme resource
Therefore, total amount of raw gas is
But the resource availability is
Now, the total production time from the provided table is
But the resource production time is
Now, regular resource can store up to 9 tones. Therefore,
And, premium resource can store up to 6 tones. Therefore,
Also, supreme resource can store up to 5 tones. Therefore,
Since, the amount of resource cannot be negative. Therefore, the positivity constraints are,
Now, the company makes profits of
Subject to the constraints:
(b)
The solution of the linear programming problem,
Subject to the constraints:
By the Simplex method.
(b)
Answer to Problem 2P
Solution:
The values of variables are
Explanation of Solution
Given Information:
The linear programming problem,
Subject to the constraints:
Consider the provided linear programming problem,
Subject to the constraints:
First convert the above problem to standard form by adding slack variables.
As the constraints are subjected to less than condition, non- negative slack variables are added to reach equality.
Let the slack variables be
Thus, the linear programming model would be:
Subject to the constraints:
The above linear programming models consist of three non-basic variables
Now the apply the Simplex method and solve the above problem as:
| Basic | x | y | z | Solution | Intercept |
||||||
| 1 | -150 | -175 | -250 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 7 | 11 | 15 | 1 | 0 | 0 | 0 | 0 | 154 | 10.2667 | |
| 0 | 10 | 8 | 12 | 0 | 1 | 0 | 0 | 0 | 80 | 6.66667 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 9 | ∞ | |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 6 | ∞ | |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 5 | 5 |
The negative minimum, P is
The minimum ratio is 5 and it corresponds to basis variable S5. So, the leaving variable is S5.
Therefore, the pivot element is 1.
| Basic | x | y | z | Solution | Intercept |
||||||
| 1 | -150 | -175 | 0 | 0 | 0 | 0 | 0 | 250 | 1250 | ||
| 0 | 7 | 11 | 0 | 1 | 0 | 0 | 0 | -15 | 79 | 7.18182 | |
| 0 | 10 | 8 | 0 | 0 | 1 | 0 | 0 | -12 | 20 | 2.5 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 9 | ∞ | |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 6 | 6 | |
| z | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 5 | ∞ |
The negative minimum, P is
The minimum ratio is 2.5 and it corresponds to basis variable S2. So, the leaving variable is S2.
Therefore, the pivot element is 8.
| Basic | x | y | z | Solution | Intercept |
||||||
| 1 | 68.75 | 0 | 0 | 0 | 21.88 | 0 | 0 | -12.5 | 1687.5 | ||
| 0 | -6.75 | 0 | 0 | 1 | -1.375 | 0 | 0 | 1.5 | 51.5 | 34.3333 | |
| y | 0 | 1.25 | 1 | 0 | 0 | 0.125 | 0 | 0 | -1.5 | 2.5 | -1.66667 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 9 | ∞ | |
| 0 | -1.25 | 0 | 0 | 0 | -0.125 | 0 | 1 | 1.5 | 3.5 | 2.33333 | |
| z | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 5 | 5 |
The negative minimum, P is
The minimum positive ratio is 2.33333 and it corresponds to basis variable S4. So, the leaving variable is S4.
Therefore, the pivot element is 1.5.
| Basic | x | y | z | Solution | ||||||
| 1 | 58.3333 | 0 | 0 | 0 | 20.83 | 0 | 8.33 | 0 | 1716.7 | |
| 0 | -5.5 | 0 | 0 | 1 | -1.25 | 0 | -1 | 0 | 48 | |
| y | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 6 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 9 | |
| 0 | -0.8333 | 0 | 0 | 0 | -0.083 | 0 | 0.67 | 1 | 2.3333 | |
| z | 0 | 0.83333 | 0 | 1 | 0 | 0.083 | 0 | -0.67 | 0 | 2.6667 |
Since
Hence, the values of variables are
(c)
The solution of the linear programming problem,
Subject to the constraints:
By the use of software.
(c)
Answer to Problem 2P
Solution:
The maximum profit is 1716.7 with
Explanation of Solution
Given Information:
The linear programming problem,
Subject to the constraints:
Use excel solver as below, to solve the linear programming,
Step 1: Enter the coefficients of x, y and z for each constraint as below,
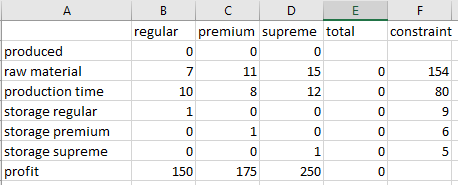
Step 2: Use formulas in column E to find total are as below,
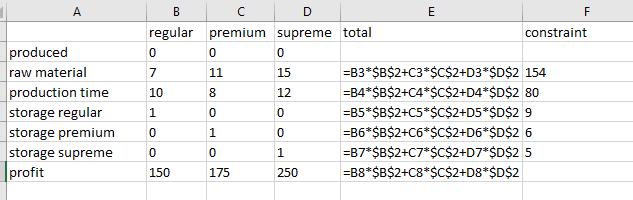
Step 3: click on Solver button under the Data Ribbon. Set the values in the Solver dialogue box as below:
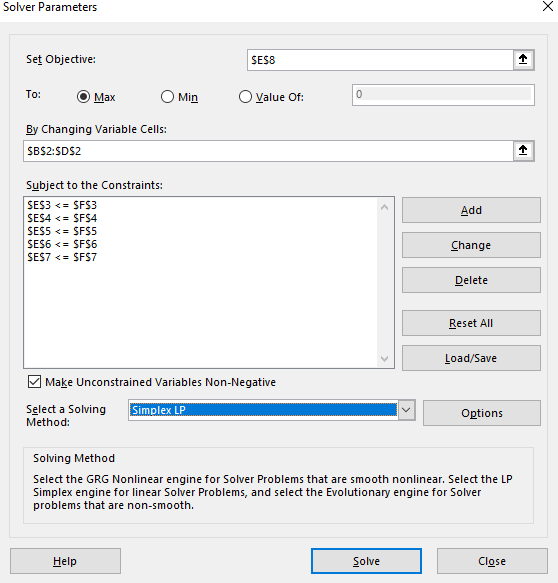
Step 4: Press the solve button.
The result obtained as,
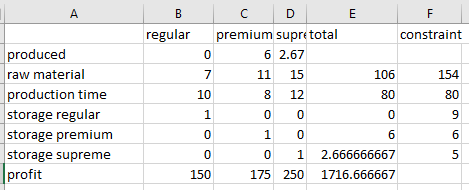
Hence, the maximum value profit is 1716.7 with
(d)
The constraint among increasing raw material, storage or production time that gives the maximum profit.
(d)
Answer to Problem 2P
Solution:
The increasing production time will give the maximum profit.
Explanation of Solution
Given Information:
The linear programming problem,
Subject to the constraints:
To obtain the maximum profit, the shadow price should be high.
Use excel as below to find the shadow price by generating the sensitivity report,
Follow same steps up to the step 4 of part (d) then select the report as sensitivity as below,
The sensitivity report for the linear programming problem is as follows,
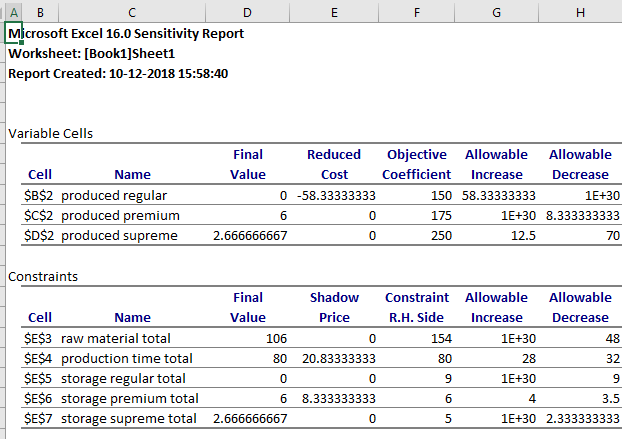
From the above sensitivity report, it is observed that the production time has a high shadow price.
Hence, the production time will give the maximum profit.
Want to see more full solutions like this?
Chapter 15 Solutions
Numerical Methods For Engineers, 7 Ed
- Find all positive integers n such that n.2n +1 is a square.arrow_forwardA straight-line H is tangent to the function g(x)=-6x-3+ 8 and passes through the point (- 4,7). Determine, the gradient of the straight-line Choose.... y-intercept of the straight-line Choose... + which of the following is the answers -1.125 -6.72 1.125 7.28 0.07 - 7.28 6.72arrow_forwardYou are required to match the correct response to each statement provided. Another term/word that can be used synonymously to Choose... gradient. A term/phrase that is associated with Arithmetic Progression. Common difference → An identity matrix can be referred to as a Choose... ÷ What is the inequality sign that represents "at most"? VIarrow_forward
- Complex Analysis 2 First exam Q1: Evaluate f the Figure. 23+3 z(z-i)² 2024-2025 dz, where C is the figure-eight contour shown in C₂arrow_forwardQ/ Find the Laurent series of (2-3) cos around z = 1 2-1arrow_forward31.5. Let be the circle |+1| = 2 traversed twice in the clockwise direction. Evaluate dz (22 + 2)²arrow_forward
- Using FDF, BDF, and CDF, find the first derivative; 1. The distance x of a runner from a fixed point is measured (in meters) at an interval of half a second. The data obtained is: t 0 x 0 0.5 3.65 1.0 1.5 2.0 6.80 9.90 12.15 Use CDF to approximate the runner's velocity at times t = 0.5s and t = 1.5s 2. Using FDF, BDF, and CDF, find the first derivative of f(x)=x Inx for an input of 2 assuming a step size of 1. Calculate using Analytical Solution and Absolute Relative Error: = True Value - Approximate Value| x100 True Value 3. Given the data below where f(x) sin (3x), estimate f(1.5) using Langrage Interpolation. x 1 1.3 1.6 1.9 2.2 f(x) 0.14 -0.69 -0.99 -0.55 0.31 4. The vertical distance covered by a rocket from t=8 to t=30 seconds is given by: 30 x = Loo (2000ln 140000 140000 - 2100 9.8t) dt Using the Trapezoidal Rule, n=2, find the distance covered. 5. Use Simpson's 1/3 and 3/8 Rule to approximate for sin x dx. Compare the results for n=4 and n=8arrow_forward1. A Blue Whale's resting heart rate has period that happens to be approximately equal to 2π. A typical ECG of a whale's heartbeat over one period may be approximated by the function, f(x) = 0.005x4 2 0.005x³-0.364x² + 1.27x on the interval [0, 27]. Find an nth-order Fourier approximation to the Blue Whale's heartbeat, where n ≥ 3 is different from that used in any other posts on this topic, to generate a periodic function that can be used to model its heartbeat, and graph your result. Be sure to include your chosen value of n in your Subject Heading.arrow_forward7. The demand for a product, in dollars, is p = D(x) = 1000 -0.5 -0.0002x² 1 Find the consumer surplus when the sales level is 200. [Hints: Let pm be the market price when xm units of product are sold. Then the consumer surplus can be calculated by foam (D(x) — pm) dx]arrow_forward
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,






