Excursions in Modern Mathematics (9th Edition)
9th Edition
ISBN: 9780134468372
Author: Peter Tannenbaum
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 15, Problem 1E
Exercises 1 through 4 refer to the data set shown in Table 15-12. The table shows the scores on a Chem 103 test consisting of 10 questions worth 10 points each.
Chem 103 test scores.
Table 15-12
Chem 103 test scores
| Student ID | Score | Student ID | Score |
| 1362 | 50 | 4315 | 70 |
| 1486 | 70 | 4719 | 70 |
| 1721 | 80 | 4951 | 60 |
| 1932 | 60 | 5321 | 60 |
| 2489 | 70 | 5872 | 100 |
| 2766 | 10 | 6433 | 50 |
| 2877 | 80 | 6921 | 50 |
| 2964 | 60 | 8317 | 70 |
| 3217 | 70 | 8854 | 100 |
| 3588 | 80 | 8964 | 80 |
| 3780 | 80 | 9158 | 60 |
| 3921 | 60 | 9347 | 60 |
| 4107 | 40 |
a. Make a frequency table for the Chem 103 test scores.
b. Draw a bar graph for the data in Table 15-12.
Expert Solution
To determine
a.
To find:
The frequency table for the Chem 103 test scores.
Answer to Problem 1E
Solution:
The frequency table for the Chem 103 test scores is given by,
| Score | Frequency |
| 10 | 1 |
| 40 | 1 |
| 50 | 3 |
| 60 | 7 |
| 70 | 6 |
| 80 | 5 |
| 100 | 2 |
Explanation of Solution
Given:
The table below shows the scores on a Chem 103 test consisting of 10 questions worth 10 points each.
| Student ID | Score | Student ID | Score |
| 1362 | 50 | 4315 | 70 |
| 1486 | 70 | 4719 | 70 |
| 1721 | 80 | 4951 | 60 |
| 1932 | 60 | 5321 | 60 |
| 2489 | 70 | 5872 | 100 |
| 2766 | 10 | 6433 | 50 |
| 2877 | 80 | 6921 | 50 |
| 2964 | 60 | 8317 | 70 |
| 3217 | 70 | 8854 | 100 |
| 3588 | 80 | 8964 | 80 |
| 3780 | 80 | 9158 | 60 |
| 3921 | 60 | 9347 | 60 |
| 4107 | 40 |
A frequency table is a table with the frequency of each actual value in the data set.
Approach:
From the given table the number of students with a score of 10 is 1, so the frequency of score 10 is 1, similarly the number of students with a score of 40 is 1, so the frequency of score 40 is 1 similarly frequencies for rest of scores can be computed.
The frequency table for the Chem 103 test is given by,
| Score | Frequency |
| 10 | 1 |
| 40 | 1 |
| 50 | 3 |
| 60 | 7 |
| 70 | 6 |
| 80 | 5 |
| 100 | 2 |
Expert Solution
To determine
b)
To construct:
The bar graph corresponding to the given table.
Answer to Problem 1E
Solution:
The bar graph is given below.
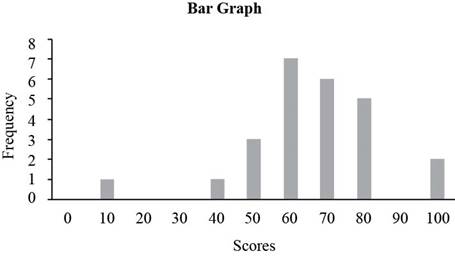
Explanation of Solution
Given:
The table below shows the scores on a Chem 103 test consisting of 10 questions worth 10 points each.
| Student ID | Score | Student ID | Score |
| 1362 | 50 | 4315 | 70 |
| 1486 | 70 | 4719 | 70 |
| 1721 | 80 | 4951 | 60 |
| 1932 | 60 | 5321 | 60 |
| 2489 | 70 | 5872 | 100 |
| 2766 | 10 | 6433 | 50 |
| 2877 | 80 | 6921 | 50 |
| 2964 | 60 | 8317 | 70 |
| 3217 | 70 | 8854 | 100 |
| 3588 | 80 | 8964 | 80 |
| 3780 | 80 | 9158 | 60 |
| 3921 | 60 | 9347 | 60 |
| 4107 | 40 |
A bar graph is a graph with bars (column) representing each of the actual values in the data set. The height of each column represents the frequency of the value in the data set.
Approach:
From the given table the number of students with a score of 0 is 0, so the frequency of score 0 is 0, similarly the number of students with a score of 10 is 1, so the frequency of score 10 is 1 similarly frequencies for rest of scores can be computed.
The frequency table for the Chem 103 test is given by,
| Score | Frequency |
| 0 | 0 |
| 10 | 1 |
| 20 | 0 |
| 30 | 0 |
| 40 | 1 |
| 50 | 3 |
| 60 | 7 |
| 70 | 6 |
| 80 | 5 |
| 90 | 0 |
| 100 | 2 |
Place the scores along horizontal axis and the frequencies along vertical axis to construct bar graph. The bar graph of the frequency table is given below.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
4.
Select all of the solutions for x²+x - 12 = 0?
A. -12
B. -4
C. -3
D. 3
E 4
F 12
4 of 10
2.
Select all of the polynomials with the degree of 7.
A. h(x) = (4x + 2)³(x − 7)(3x + 1)4
B
h(x) = (x + 7)³(2x + 1)^(6x − 5)²
☐
Ch(x)=(3x² + 9)(x + 4)(8x + 2)ª
h(x) = (x + 6)²(9x + 2) (x − 3)
h(x)=(-x-7)² (x + 8)²(7x + 4)³
Scroll down to see more
2 of 10
1.
If all of the zeros for a polynomial are included in the graph, which polynomial could the graph represent?
100
-6
-2
0
2
100
200
Chapter 15 Solutions
Excursions in Modern Mathematics (9th Edition)
Ch. 15 - Exercises 1 through 4 refer to the data set shown...Ch. 15 - Exercises 1 through 4 refer to the data set shown...Ch. 15 - Exercises 1 through 4 refer to the data set shown...Ch. 15 - Exercises 1 through 4 refer to the data set shown...Ch. 15 - Exercises 5 through 10 refer to Table 15-13, which...Ch. 15 - Exercises 5 through 10 refer to Table 15-13, which...Ch. 15 - Exercises 5 through 10 refer to Table 15-13, which...Ch. 15 - Exercise 5 through 10 refer to Table 15-13, which...Ch. 15 - Exercise 5 through 10 refer to Table 15-13, which...Ch. 15 - Exercise 5 through 10 refer to Table 15-13, which...
Ch. 15 - Exercise 11 and 12 refer to the bar graph shown in...Ch. 15 - Exercise 11 and 12 refer to the bar graph shown in...Ch. 15 - Exercise 13 and 14 refer to the pie chart in Fig....Ch. 15 - Exercise 13 and 14 refer to the pie chart in Fig....Ch. 15 - Table 15-14 shows the class interval frequencies...Ch. 15 - Table 15-15 shows the class interval frequencies...Ch. 15 - Table 15-16 shows the percentage of U.S. working...Ch. 15 - Table 15-17 shows the percentage of U.S. workers...Ch. 15 - Exercises 19 and 20 refer to Table 15-18, which...Ch. 15 - More than Less than or equal to Number of babies...Ch. 15 - Exercises 21 and 22 refer to the two histograms...Ch. 15 - Exercises 21 and 22 refer to the two histograms...Ch. 15 - Consider the data set {3,5,7,4,8,2,8,3,6}. a.Find...Ch. 15 - Consider the data set {4,6,8,5.2,10.4,10,12.6,13}...Ch. 15 - Find the average A and median M of each of the...Ch. 15 - Find the average A and median M of each of the...Ch. 15 - Find the average A and median M of each of the...Ch. 15 - Find the average A and median M of each of the...Ch. 15 - Table 15-19 shows the results of a 5-point musical...Ch. 15 - Table 15-20 shows the ages of the firefighters in...Ch. 15 - Table 15-21 shows the relative frequencies of the...Ch. 15 - Table 15-22 shows the relative frequencies of the...Ch. 15 - Consider the data set {5,7,4,8,2,8,3,6}. a. Find...Ch. 15 - Consider the data set {4,6,8,5.2,10.4,10,12.6,13}....Ch. 15 - For each data set, find the 75th and the 90th...Ch. 15 - For each data set, find the 10th and the 25th...Ch. 15 - Table 15-20 Age 25 27 28 29 30 Frequency 2 7 6 9...Ch. 15 - This exercise refers to the math quiz scores shown...Ch. 15 - Prob. 39ECh. 15 - Exercise 39 and 40 refer to SAT test scores for...Ch. 15 - Consider the data set {5,7,4,8,2,8,3,6}. a. Find...Ch. 15 - Consider the data set {4,6,8,5.2,10.4,10,12.6,13}....Ch. 15 - Prob. 43ECh. 15 - This exercise refers to the distribution of the...Ch. 15 - Exercises 45 and 46 refer to the two box plots in...Ch. 15 - Exercises 45 and 46 refer to the two box plots in...Ch. 15 - For the data set {5,7,4,8,2,8,3,6}, find a. the...Ch. 15 - For the data set {4,6,8,5.2,10.4,10,12.6,13}, find...Ch. 15 - A realty company has sold N=341 homes in the last...Ch. 15 - Exercise 45 and 46 refer to the box plot in...Ch. 15 - Prob. 51ECh. 15 - For Exercises 51 through 54, you should use the...Ch. 15 - For Exercises 51 through 54, you should use the...Ch. 15 - For Exercises 51 through 54, you should use the...Ch. 15 - The purpose of Exercises 55 and 56 is to practice...Ch. 15 - The purpose of Exercises 55 and 56 is to practice...Ch. 15 - Exercises 57 and 58 refer to the mode of a data...Ch. 15 - Exercises 57 and 58 refer to the mode of a data...Ch. 15 - Mikes average on the first five exams in Econ 1A...Ch. 15 - Explain each of the following statements regarding...Ch. 15 - In 2006, the median SAT score was the average of...Ch. 15 - In 2004, the third quartile SAT scores was...Ch. 15 - Prob. 63ECh. 15 - Suppose that the average of 10 numbers is 7.5 and...Ch. 15 - Prob. 65ECh. 15 - What happens to the five-number summary of the...Ch. 15 - Prob. 67ECh. 15 - Prob. 68ECh. 15 - Prob. 69ECh. 15 - Prob. 70ECh. 15 - Prob. 71ECh. 15 - Prob. 72ECh. 15 - Prob. 73ECh. 15 - Suppose that the standard deviation of the data...Ch. 15 - Chebyshevs theorem. The Russian mathematician P.L....
Additional Math Textbook Solutions
Find more solutions based on key concepts
1. How much money is Joe earning when he’s 30?
Pathways To Math Literacy (looseleaf)
For Problems 23-28, write in simpler form, as in Example 4. logbFG
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Empirical versus Theoretical A Monopoly player claims that the probability of getting a 4 when rolling a six-si...
Introductory Statistics
The largest polynomial that divides evenly into a list of polynomials is called the _______.
Elementary & Intermediate Algebra
Fill in each blank so that the resulting statement is true.
1. The degree of the polynomial function is _____....
Algebra and Trigonometry (6th Edition)
First Derivative Test a. Locale the critical points of f. b. Use the First Derivative Test to locale the local ...
Calculus: Early Transcendentals (2nd Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 3. Select the polynomial that matches the description given: Zero at 4 with multiplicity 3 Zero at −1 with multiplicity 2 Zero at -10 with multiplicity 1 Zero at 5 with multiplicity 5 ○ A. P(x) = (x − 4)³(x + 1)²(x + 10)(x — 5)³ B - P(x) = (x + 4)³(x − 1)²(x − 10)(x + 5)³ ○ ° P(x) = (1 − 3)'(x + 2)(x + 1)"'" (x — 5)³ 51 P(r) = (x-4)³(x − 1)(x + 10)(x − 5 3 of 10arrow_forwardMatch the equation, graph, and description of transformation. Horizontal translation 1 unit right; vertical translation 1 unit up; vertical shrink of 1/2; reflection across the x axis Horizontal translation 1 unit left; vertical translation 1 unit down; vertical stretch of 2 Horizontal translation 2 units right; reflection across the x-axis Vertical translation 1 unit up; vertical stretch of 2; reflection across the x-axis Reflection across the x - axis; vertical translation 2 units down Horizontal translation 2 units left Horizontal translation 2 units right Vertical translation 1 unit down; vertical shrink of 1/2; reflection across the x-axis Vertical translation 2 units down Horizontal translation 1 unit left; vertical translation 2 units up; vertical stretch of 2; reflection across the x - axis f(x) = - =-½ ½ (x − 1)²+1 f(x) = x²-2 f(x) = -2(x+1)²+2 f(x)=2(x+1)²-1 f(x)=-(x-2)² f(x)=(x-2)² f(x) = f(x) = -2x²+1 f(x) = -x²-2 f(x) = (x+2)²arrow_forwardWhat is the vertex, increasing interval, decreasing interval, domain, range, root/solution/zero, and the end behavior?arrow_forward
- Calculate a (bxc) where a = i, b = j, and c = k.arrow_forwardi+2j+3k = (1,2,3) and b = -i-k. Calculate the cross product a x b where a Next calculate the area of the parallelogram spanned by a and b.arrow_forwardThe measured receptance data around two resonant picks of a structure are tabulated in the followings. Find the natural frequencies, damping ratios, and mode shapes of the structure. (30 points) (@)×10 m/N α₁₂ (@)×10 m/N w/2z (Hz) 99 0.1176 0.17531 0.1114 -0.1751i 101 -0.0302 0.2456i -0.0365 -0.2453i 103 -0.1216 0.1327i -0.1279-0.1324i 220 0.0353 0.0260i -0.0419+0.0259i 224 0.0210 0.0757i |-0.0273 +0.0756i 228 -0.0443 0.0474i 0.0382 +0.0474iarrow_forward
- Q3: Define the linear functional J: H(2) R by 1(v) = a(v. v) - L(v) Let u be the unique weak solution to a(u,v) = L(v) in H() and suppose that a(...) is a symmetric bilinear form on H(2) prove that 1- u is minimizer. 2- u is unique. 3- The minimizer J(u,) can be rewritten under algebraic form u Au-ub. J(u)=u'Au- Where A. b are repictively the stiffence matrix and the load vectorarrow_forward== 1. A separable differential equation can be written in the form hy) = g(a) where h(y) is a function of y only, and g(x) is a function of r only. All of the equations below are separable. Rewrite each of these in the form h(y) = g(x), then find a general solution by integrating both sides. Determine whether the solutions you found are explicit (functions) or implicit (curves but not functions) (a) 1' = — 1/3 (b) y' = = --- Y (c) y = x(1+ y²)arrow_forwardJa дх dx dx Q3: Define the linear functional J: H()-R by تاریخ (v) = ½a(v, v) - (v) == Let u be the unique weak solution to a(u,v) = L(v) in H₁(2) and suppose that a(...) is a symmetric bilinear form on H() prove that a Buy v) = 1- u is minimizer. 2- u is unique. 3- The minimizer J(u,) can be rewritten under J(u)=u' Au-ub, algebraic form Where A, b are repictively the stiffence matrix and the load vector Q4: A) Answer only 1-show that thelation to -Auf in N, u = 0 on a satisfies the stability Vulf and show that V(u-u,)||² = ||vu||2 - ||vu||2 lu-ulls Chu||2 2- Prove that Where =1 ||ul|= a(u, u) = Vu. Vu dx + fu. uds B) Consider the bilinear form a(u, v) = (Au, Av) + (Vu, Vv) + (Vu, v) + (u, v) Show that a(u, v) continues and V- elliptic on H(2) (3) (0.0), (3.0)arrow_forward
- Q1: A) fill the following: 1- The number of triangular in a triangular region with 5 nodes is quadrilateral with n=5 and m=6 nodés is 2- The complex shape function in 1-D 3- dim(P4(K))=- (7M --- and in the and multiplex shape function in 2-D is 4- The trial space and test space for problem -Auf, u = go on and B) Define the energy norm and prove that the solution u, defined by Galerkin orthogonal satisfies the best approximation. Q2: A) Find the varitional form for the problem 1330 (b(x)) - x²=0, 0arrow_forwardDescribe a three step process you choose to determine how many elementary schools there are in the city of 5 million people.arrow_forwardA circle of radius r centered at the point (0,r) in the plane will intersect the y-axis at the origin and the point A=(0,2r), as pictured below. A line passes through the point A and the point C=(11/2,0) on the x-axis. In this problem, we will investigate the coordinates of the intersection point B between the circle and the line, as 1 → ∞ A=(0,2r) B (0,0) (a) The line through A and C has equation: y= 2 117 x+27 (b) The x-coordinate of the point B is 4472 121,2 +4 40 (c) The y-coordinate of the point B is +27 121 44 (d) The limit as r→ ∞ of the x-coordinate of B is 121 (if your answer is oo, write infinity).arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
The Shape of Data: Distributions: Crash Course Statistics #7; Author: CrashCourse;https://www.youtube.com/watch?v=bPFNxD3Yg6U;License: Standard YouTube License, CC-BY
Shape, Center, and Spread - Module 20.2 (Part 1); Author: Mrmathblog;https://www.youtube.com/watch?v=COaid7O_Gag;License: Standard YouTube License, CC-BY
Shape, Center and Spread; Author: Emily Murdock;https://www.youtube.com/watch?v=_YyW0DSCzpM;License: Standard Youtube License