Connect Math hosted by ALEKS Access Card 52 Weeks for Math in Our World
3rd Edition
ISBN: 9781259232848
Author: David Sobecki, Allan Bluman
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 14.2, Problem 20E
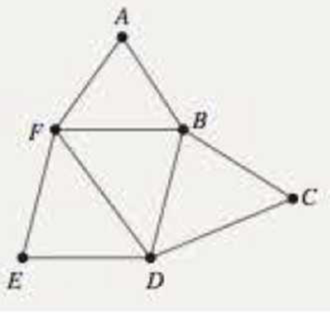
For Exercises 11–20,
(a) State whether the graph has an Euler path, an Euler circuit, or neither
(b) If the graph has an Euler path or an Euler circuit, find one.
20. 
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Jamal wants to save $48,000 for a down payment on a home. How much will he need to invest in an
account with 11.8% APR, compounding daily, in order to reach his goal in 10 years? Round to the
nearest dollar.
r
nt
Use the compound interest formula, A (t) = P(1 + 1)".
An account is opened with an intial deposit of $7,500 and earns 3.8% interest compounded semi-
annually. Round all answers to the nearest dollar.
a. What will the account be worth in 10 years? $
b. What if the interest were compounding monthly? $
c. What if the interest were compounded daily (assume 365 days in a year)? $
Kyoko has $10,000 that she wants to invest. Her bank has several accounts to choose from. Her goal is
to have $15,000 by the time she finishes graduate school in 7 years. To the nearest hundredth of a
percent, what should her minimum annual interest rate be in order to reach her goal assuming they
compound daily? (Hint: solve the compound interest formula for the intrerest rate. Also, assume there
are 365 days in a year)
%
Chapter 14 Solutions
Connect Math hosted by ALEKS Access Card 52 Weeks for Math in Our World
Ch. 14.1 - Draw a graph to represent ferry service between...Ch. 14.1 - The floor plan shown in Figure 14-7 is for a...Ch. 14.1 - Prob. 3TTOCh. 14.1 - Draw a graph for my neighborhood, shown in Figure...Ch. 14.1 - Prob. 5TTOCh. 14.1 - Prob. 6TTOCh. 14.1 - Prob. 7TTOCh. 14.1 - Prob. 8TTOCh. 14.1 - Prob. 1ECh. 14.1 - What is the difference between a loop and a...
Ch. 14.1 - What is the difference between a circuit and a...Ch. 14.1 - Draw two graphs that look physically different but...Ch. 14.1 - Prob. 5ECh. 14.1 - Prob. 8ECh. 14.1 - Prob. 9ECh. 14.1 - Prob. 10ECh. 14.1 - Prob. 11ECh. 14.1 - How does graph coloring apply to maps?Ch. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Prob. 18ECh. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Prob. 20ECh. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Prob. 25ECh. 14.1 - Prob. 26ECh. 14.1 - Prob. 27ECh. 14.1 - Prob. 28ECh. 14.1 - Prob. 29ECh. 14.1 - Prob. 30ECh. 14.1 - For Exercises 3134, represent each figure using a...Ch. 14.1 - Prob. 32ECh. 14.1 - Prob. 33ECh. 14.1 - Prob. 34ECh. 14.1 - Prob. 35ECh. 14.1 - Prob. 36ECh. 14.1 - For Exercises 3538, draw a graph to represent each...Ch. 14.1 - Prob. 38ECh. 14.1 - Prob. 39ECh. 14.1 - For Exercises 3942, draw a graph that represents...Ch. 14.1 - Prob. 41ECh. 14.1 - Prob. 42ECh. 14.1 - In Exercises 4350, use graph coloring to find the...Ch. 14.1 - Prob. 44ECh. 14.1 - Prob. 45ECh. 14.1 - Prob. 46ECh. 14.1 - In Exercises 4350, use graph coloring to find the...Ch. 14.1 - Prob. 48ECh. 14.1 - Prob. 49ECh. 14.1 - Prob. 50ECh. 14.1 - Prob. 51ECh. 14.1 - Prob. 52ECh. 14.1 - Prob. 53ECh. 14.1 - Prob. 54ECh. 14.1 - Prob. 55ECh. 14.1 - Draw a graph that represents the street map in...Ch. 14.1 - Prob. 57ECh. 14.1 - Prob. 58ECh. 14.1 - Prob. 59ECh. 14.1 - Prob. 61ECh. 14.1 - Prob. 62ECh. 14.1 - Prob. 63ECh. 14.1 - (a)When a graph represents a map as in Exercise...Ch. 14.2 - Use Eulers theorem to determine if the graphs...Ch. 14.2 - Prob. 2TTOCh. 14.2 - Prob. 3TTOCh. 14.2 - Prob. 1ECh. 14.2 - Prob. 2ECh. 14.2 - Prob. 3ECh. 14.2 - Prob. 4ECh. 14.2 - Prob. 5ECh. 14.2 - Prob. 6ECh. 14.2 - For Exercises 710, decide whether each connected...Ch. 14.2 - Prob. 8ECh. 14.2 - For Exercises 710, decide whether each connected...Ch. 14.2 - Prob. 10ECh. 14.2 - For Exercises 1120, (a)State whether the graph has...Ch. 14.2 - Prob. 12ECh. 14.2 - For Exercises 1120, (a)State whether the graph has...Ch. 14.2 - Prob. 14ECh. 14.2 - For Exercises 1120, (a)State whether the graph has...Ch. 14.2 - Prob. 16ECh. 14.2 - For Exercises 1120, (a)State whether the graph has...Ch. 14.2 - Prob. 18ECh. 14.2 - For Exercises 1120, (a)State whether the graph has...Ch. 14.2 - For Exercises 1120, (a)State whether the graph has...Ch. 14.2 - Prob. 21ECh. 14.2 - Prob. 22ECh. 14.2 - Prob. 23ECh. 14.2 - Prob. 24ECh. 14.2 - Prob. 25ECh. 14.2 - For Exercises 2126, draw a graph for the figures...Ch. 14.2 - Prob. 27ECh. 14.2 - Prob. 28ECh. 14.2 - Prob. 29ECh. 14.2 - Prob. 30ECh. 14.2 - Prob. 31ECh. 14.2 - Prob. 32ECh. 14.2 - For Exercises 33 and 34, determine if an Euler...Ch. 14.2 - For Exercises 33 and 34, determine if an Euler...Ch. 14.2 - Prob. 35ECh. 14.2 - Prob. 37ECh. 14.2 - Prob. 38ECh. 14.2 - Draw some sample graphs and use them to discuss...Ch. 14.2 - Prob. 40ECh. 14.2 - Prob. 41ECh. 14.2 - Prob. 42ECh. 14.2 - Explain why the word connected is crucial...Ch. 14.2 - Prob. 44ECh. 14.2 - Prob. 45ECh. 14.2 - Prob. 46ECh. 14.3 - Find a Hamilton path that begins at vertex C for...Ch. 14.3 - Prob. 2TTOCh. 14.3 - Prob. 3TTOCh. 14.3 - The driving times in minutes between four cities...Ch. 14.3 - Prob. 5TTOCh. 14.3 - Prob. 6TTOCh. 14.3 - Prob. 7TTOCh. 14.3 - What is the difference between a Hamilton path and...Ch. 14.3 - Prob. 2ECh. 14.3 - Give an example of a problem in our world that can...Ch. 14.3 - Prob. 4ECh. 14.3 - Prob. 5ECh. 14.3 - Prob. 6ECh. 14.3 - Describe what a typical traveling salesperson...Ch. 14.3 - Prob. 8ECh. 14.3 - Prob. 9ECh. 14.3 - Prob. 10ECh. 14.3 - For Exercises 1118, find two different Hamilton...Ch. 14.3 - Prob. 12ECh. 14.3 - Prob. 13ECh. 14.3 - Prob. 14ECh. 14.3 - For Exercises 1118, find two different Hamilton...Ch. 14.3 - Prob. 16ECh. 14.3 - Prob. 17ECh. 14.3 - Prob. 18ECh. 14.3 - For Exercises 1118, find two different Hamilton...Ch. 14.3 - Prob. 20ECh. 14.3 - Prob. 21ECh. 14.3 - Prob. 22ECh. 14.3 - For Exercises 1924, find two different Hamilton...Ch. 14.3 - Prob. 24ECh. 14.3 - Prob. 25ECh. 14.3 - Prob. 26ECh. 14.3 - For Exercises 2528, find the number of Hamilton...Ch. 14.3 - Prob. 28ECh. 14.3 - Prob. 29ECh. 14.3 - For Exercises 29 and 30, use the brute force...Ch. 14.3 - For Exercises 3134, use the nearest neighbor...Ch. 14.3 - Prob. 32ECh. 14.3 - Prob. 33ECh. 14.3 - Prob. 34ECh. 14.3 - In Exercises 3538, use the cheapest link algorithm...Ch. 14.3 - Prob. 36ECh. 14.3 - Prob. 37ECh. 14.3 - Prob. 38ECh. 14.3 - Prob. 39ECh. 14.3 - For Exercises 3942, use the information in the...Ch. 14.3 - Prob. 41ECh. 14.3 - Prob. 42ECh. 14.3 - Prob. 43ECh. 14.3 - For Exercises 4346, use the information in the...Ch. 14.3 - For Exercises 4346, use the information in the...Ch. 14.3 - Prob. 46ECh. 14.3 - Prob. 47ECh. 14.3 - A pizza delivery person has five prearranged...Ch. 14.3 - Prob. 49ECh. 14.3 - Prob. 50ECh. 14.3 - Prob. 51ECh. 14.3 - Prob. 52ECh. 14.3 - When planning routes, distance isnt always the key...Ch. 14.3 - Prob. 54ECh. 14.3 - Repeat questions 51 through 54, choosing four...Ch. 14.3 - Prob. 56ECh. 14.3 - Prob. 57ECh. 14.3 - Prob. 58ECh. 14.3 - Find a road atlas that has a mileage chart. Pick...Ch. 14.3 - Prob. 60ECh. 14.3 - Prob. 61ECh. 14.3 - Prob. 62ECh. 14.3 - Prob. 63ECh. 14.3 - Prob. 64ECh. 14.3 - Prob. 65ECh. 14.3 - Prob. 66ECh. 14.4 - Prob. 1TTOCh. 14.4 - Prob. 2TTOCh. 14.4 - Prob. 3TTOCh. 14.4 - Prob. 4TTOCh. 14.4 - Prob. 5TTOCh. 14.4 - Prob. 1ECh. 14.4 - Prob. 2ECh. 14.4 - Prob. 3ECh. 14.4 - Prob. 4ECh. 14.4 - Prob. 5ECh. 14.4 - Prob. 6ECh. 14.4 - For Exercise 716, decide whether or not each graph...Ch. 14.4 - Prob. 8ECh. 14.4 - Prob. 9ECh. 14.4 - Prob. 10ECh. 14.4 - Prob. 11ECh. 14.4 - Prob. 12ECh. 14.4 - Prob. 13ECh. 14.4 - Prob. 14ECh. 14.4 - Prob. 15ECh. 14.4 - Prob. 16ECh. 14.4 - Prob. 17ECh. 14.4 - Prob. 18ECh. 14.4 - Prob. 19ECh. 14.4 - Prob. 20ECh. 14.4 - Prob. 21ECh. 14.4 - Prob. 22ECh. 14.4 - Prob. 23ECh. 14.4 - Prob. 24ECh. 14.4 - Prob. 25ECh. 14.4 - Prob. 26ECh. 14.4 - Prob. 27ECh. 14.4 - Prob. 28ECh. 14.4 - Prob. 29ECh. 14.4 - Prob. 30ECh. 14.4 - Prob. 31ECh. 14.4 - Prob. 32ECh. 14.4 - Prob. 33ECh. 14.4 - As a new suburban neighborhood is being built, the...Ch. 14.4 - Prob. 35ECh. 14.4 - Prob. 36ECh. 14.4 - Prob. 37ECh. 14.4 - Prob. 38ECh. 14.4 - Prob. 39ECh. 14.4 - In the last two sections, we used both Hamilton...Ch. 14.4 - Prob. 41ECh. 14.4 - Prob. 42ECh. 14 - Use the graph shown in Figure 14-62 for Exercise...Ch. 14 - Prob. 2RECh. 14 - Prob. 3RECh. 14 - Prob. 4RECh. 14 - Prob. 5RECh. 14 - Prob. 6RECh. 14 - Use the graph shown in Figure 14-62 for Exercises...Ch. 14 - Prob. 8RECh. 14 - Prob. 9RECh. 14 - Prob. 10RECh. 14 - Prob. 11RECh. 14 - Prob. 12RECh. 14 - Prob. 13RECh. 14 - Repeat Exercise 13 for the graphs from Exercises...Ch. 14 - Prob. 15RECh. 14 - Prob. 16RECh. 14 - Prob. 17RECh. 14 - Prob. 18RECh. 14 - Prob. 19RECh. 14 - Prob. 20RECh. 14 - Prob. 21RECh. 14 - Prob. 22RECh. 14 - Prob. 23RECh. 14 - Prob. 24RECh. 14 - Prob. 25RECh. 14 - Prob. 26RECh. 14 - Prob. 27RECh. 14 - Prob. 28RECh. 14 - Prob. 29RECh. 14 - Prob. 30RECh. 14 - Prob. 31RECh. 14 - Prob. 32RECh. 14 - Prob. 33RECh. 14 - Prob. 34RECh. 14 - For the following graph: (a)What is the degree of...Ch. 14 - Draw a graph with two bridges, and the...Ch. 14 - Prob. 3CTCh. 14 - Prob. 4CTCh. 14 - (a)For the graph shown in Figure 14-73, find an...Ch. 14 - Prob. 6CTCh. 14 - For the housing plan shown in Figure 14-75, draw a...Ch. 14 - Prob. 8CTCh. 14 - Use the brute force method to find the shortest...Ch. 14 - Use the nearest neighbor method and cheapest link...Ch. 14 - Prob. 11CTCh. 14 - Decide whether the problem can be solved using...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Test the claim that a student's pulse rate is different when taking a quiz than attending a regular class. The mean pulse rate difference is 2.7 with 10 students. Use a significance level of 0.005. Pulse rate difference(Quiz - Lecture) 2 -1 5 -8 1 20 15 -4 9 -12arrow_forwardThere are three options for investing $1150. The first earns 10% compounded annually, the second earns 10% compounded quarterly, and the third earns 10% compounded continuously. Find equations that model each investment growth and use a graphing utility to graph each model in the same viewing window over a 20-year period. Use the graph to determine which investment yields the highest return after 20 years. What are the differences in earnings among the three investment? STEP 1: The formula for compound interest is A = nt = P(1 + − − ) n², where n is the number of compoundings per year, t is the number of years, r is the interest rate, P is the principal, and A is the amount (balance) after t years. For continuous compounding, the formula reduces to A = Pert Find r and n for each model, and use these values to write A in terms of t for each case. Annual Model r=0.10 A = Y(t) = 1150 (1.10)* n = 1 Quarterly Model r = 0.10 n = 4 A = Q(t) = 1150(1.025) 4t Continuous Model r=0.10 A = C(t) =…arrow_forwardThe following ordered data list shows the data speeds for cell phones used by a telephone company at an airport: A. Calculate the Measures of Central Tendency from the ungrouped data list. B. Group the data in an appropriate frequency table. C. Calculate the Measures of Central Tendency using the table in point B. D. Are there differences in the measurements obtained in A and C? Why (give at least one justified reason)? I leave the answers to A and B to resolve the remaining two. 0.8 1.4 1.8 1.9 3.2 3.6 4.5 4.5 4.6 6.2 6.5 7.7 7.9 9.9 10.2 10.3 10.9 11.1 11.1 11.6 11.8 12.0 13.1 13.5 13.7 14.1 14.2 14.7 15.0 15.1 15.5 15.8 16.0 17.5 18.2 20.2 21.1 21.5 22.2 22.4 23.1 24.5 25.7 28.5 34.6 38.5 43.0 55.6 71.3 77.8 A. Measures of Central Tendency We are to calculate: Mean, Median, Mode The data (already ordered) is: 0.8, 1.4, 1.8, 1.9, 3.2, 3.6, 4.5, 4.5, 4.6, 6.2, 6.5, 7.7, 7.9, 9.9, 10.2, 10.3, 10.9, 11.1, 11.1, 11.6, 11.8, 12.0, 13.1, 13.5, 13.7, 14.1, 14.2, 14.7, 15.0, 15.1, 15.5,…arrow_forward
- A tournament is a complete directed graph, for each pair of vertices x, y either (x, y) is an arc or (y, x) is an arc. One can think of this as a round robin tournament, where the vertices represent teams, each pair plays exactly once, with the direction of the arc indicating which team wins. (a) Prove that every tournament has a direct Hamiltonian path. That is a labeling of the teams V1, V2,..., Un so that vi beats Vi+1. That is a labeling so that team 1 beats team 2, team 2 beats team 3, etc. (b) A digraph is strongly connected if there is a directed path from any vertex to any other vertex. Equivalently, there is no partition of the teams into groups A, B so that every team in A beats every team in B. Prove that every strongly connected tournament has a directed Hamiltonian cycle. Use this to show that for any team there is an ordering as in part (a) for which the given team is first. (c) A king in a tournament is a vertex such that there is a direct path of length at most 2 to any…arrow_forwardUse a graphing utility to find the point of intersection, if any, of the graphs of the functions. Round your result to three decimal places. (Enter NONE in any unused answer blanks.) y = 100e0.01x (x, y) = y = 11,250 ×arrow_forwardhow to construct the following same table?arrow_forward
- The following is known. The complete graph K2t on an even number of vertices has a 1- factorization (equivalently, its edges can be colored with 2t - 1 colors so that the edges incident to each vertex are distinct). This implies that the complete graph K2t+1 on an odd number of vertices has a factorization into copies of tK2 + K₁ (a matching plus an isolated vertex). A group of 10 people wants to set up a 45 week tennis schedule playing doubles, each week, the players will form 5 pairs. One of the pairs will not play, the other 4 pairs will each play one doubles match, two of the pairs playing each other and the other two pairs playing each other. Set up a schedule with the following constraints: Each pair of players is a doubles team exactly 4 times; during those 4 matches they see each other player exactly once; no two doubles teams play each other more than once. (a) Find a schedule. Hint - think about breaking the 45 weeks into 9 blocks of 5 weeks. Use factorizations of complete…arrow_forward. The two person game of slither is played on a graph. Players 1 and 2 take turns, building a path in the graph. To start, Player 1 picks a vertex. Player 2 then picks an edge incident to the vertex. Then, starting with Player 1, players alternate turns, picking a vertex not already selected that is adjacent to one of the ends of the path created so far. The first player who cannot select a vertex loses. (This happens when all neighbors of the end vertices of the path are on the path.) Prove that Player 2 has a winning strategy if the graph has a perfect matching and Player 1 has a winning strategy if the graph does not have a perfect matching. In each case describe a strategy for the winning player that guarantees that they will always be able to select a vertex. The strategy will be based on using a maximum matching to decide the next choice, and will, for one of the cases involve using the fact that maximality means no augmenting paths. Warning, the game slither is often described…arrow_forwardLet D be a directed graph, with loops allowed, for which the indegree at each vertex is at most k and the outdegree at each vertex is at most k. Prove that the arcs of D can be colored so that the arcs entering each vertex must have distinct colors and the arcs leaving each vertex have distinct colors. An arc entering a vertex may have the same color as an arc leaving it. It is probably easiest to make use of a known result about edge coloring. Think about splitting each vertex into an ‘in’ and ‘out’ part and consider what type of graph you get.arrow_forward
- 3:56 wust.instructure.com Page 0 Chapter 5 Test Form A of 2 - ZOOM + | Find any real numbers for which each expression is undefined. 2x 4 1. x Name: Date: 1. 3.x-5 2. 2. x²+x-12 4x-24 3. Evaluate when x=-3. 3. x Simplify each rational expression. x²-3x 4. 2x-6 5. x²+3x-18 x²-9 6. Write an equivalent rational expression with the given denominator. 2x-3 x²+2x+1(x+1)(x+2) Perform the indicated operation and simplify if possible. x²-16 x-3 7. 3x-9 x²+2x-8 x²+9x+20 5x+25 8. 4.x 2x² 9. x-5 x-5 3 5 10. 4x-3 8x-6 2 3 11. x-4 x+4 x 12. x-2x-8 x²-4 ← -> Copyright ©2020 Pearson Education, Inc. + 5 4. 5. 6. 7. 8. 9. 10. 11. 12. T-97arrow_forwardplease work out more details give the solution.arrow_forwardProblem #5 Suppose you flip a two sided fair coin ("heads" or "tails") 8 total times. a). How many ways result in 6 tails and 2 heads? b). How many ways result in 2 tails and 6 heads? c). Compare your answers to part (a) and (b) and explain in a few sentences why the comparison makes sense.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON
Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON
Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY