6th Edition

ISBN: 9780321867322

Author: Robert F. Blitzer

Publisher: PEARSON

See similar textbooks

Videos

Textbook Question

100%

Chapter 14.1, Problem 14E

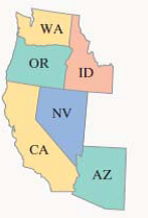
In Exercises 13-14, create a graph that models the bordering relationships among the states shown in each map. Use vertices to represent the states and edges to represent common borders.

Chapter 14.1, Problem 14E, In Exercises 13-14, create a graph that models the bordering relationships among the states shown in

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Chapter 14.1, Problem 13E

Chapter 14.1, Problem 15E

Students have asked these similar questions

5. (a) State the Residue Theorem. Your answer should include all the conditions required for the theorem to hold. (4 marks) (b) Let y be the square contour with vertices at -3, -3i, 3 and 3i, described in the anti-clockwise direction. Evaluate に dz. You must check all of the conditions of any results that you use. (5 marks) (c) Evaluate L You must check all of the conditions of any results that you use. ཙ x sin(Tx) x²+2x+5 da. (11 marks)

3. (a) Lety: [a, b] C be a contour. Let L(y) denote the length of y. Give a formula for L(y). (1 mark) (b) Let UCC be open. Let f: U→C be continuous. Let y: [a,b] → U be a contour. Suppose there exists a finite real number M such that |f(z)| < M for all z in the image of y. Prove that < ||, f(z)dz| ≤ ML(y). (3 marks) (c) State and prove Liouville's theorem. You may use Cauchy's integral formula without proof. (d) Let R0. Let w € C. Let (10 marks) U = { z Є C : | z − w| < R} . Let f UC be a holomorphic function such that 0 < |ƒ(w)| < |f(z)| for all z Є U. Show, using the local maximum modulus principle, that f is constant. (6 marks)

3. (a) Let A be an algebra. Define the notion of an A-module M. When is a module M a simple module? (b) State and prove Schur's Lemma for simple modules. (c) Let AM(K) and M = K" the natural A-module. (i) Show that M is a simple K-module. (ii) Prove that if ƒ € Endд(M) then ƒ can be written as f(m) = am, where a is a matrix in the centre of M, (K). [Recall that the centre, Z(M,(K)) == {a Mn(K) | ab M,,(K)}.] = ba for all bЄ (iii) Explain briefly why this means End₁(M) K, assuming that Z(M,,(K))~ K as K-algebras. Is this consistent with Schur's lemma?

Chapter 14 Solutions

Thinking Mathematically (6th Edition)

Ch. 14.1 - CHECK POINT 1 Explain why Figures 14.4(a) and (b)...Ch. 14.1 - CHECK POINT 2 The city of Metroville is located on...Ch. 14.1 - Prob. 3CP Ch. 14.1 - CHECK POINT 4 The floor plan of a four-room house...Ch. 14.1 - CHECK POINT 5 A security guard needs to walk the...Ch. 14.1 - CHECK POINT 6 List the pairs of adjacent vertices...Ch. 14.1 - Fill in each blank so that the resulting statement...Ch. 14.1 - Fill in each blank so that the resulting statement...Ch. 14.1 - Fill in each blank so that the resulting statement...Ch. 14.1 - Fill in each blank so that the resulting statement...

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.

In Exercises 13-14, create a graph that models the bordering relationships among the states shown in each map. Use vertices to represent the states and edges to represent common borders.

Solution Summary: The author explains that graph modelling is a pictorial representation of objects that describes the relationships among objects. The states are represented by vertices and the common border from one state to another is represented.

Videos

Want to see the full answer?

Chapter 14 Solutions