
Concept explainers
(a)
The free-body diagram of the forces acting on the ladder.
(a)
Answer to Problem 82PQ
The free-body diagram of the forces acting on the ladder is
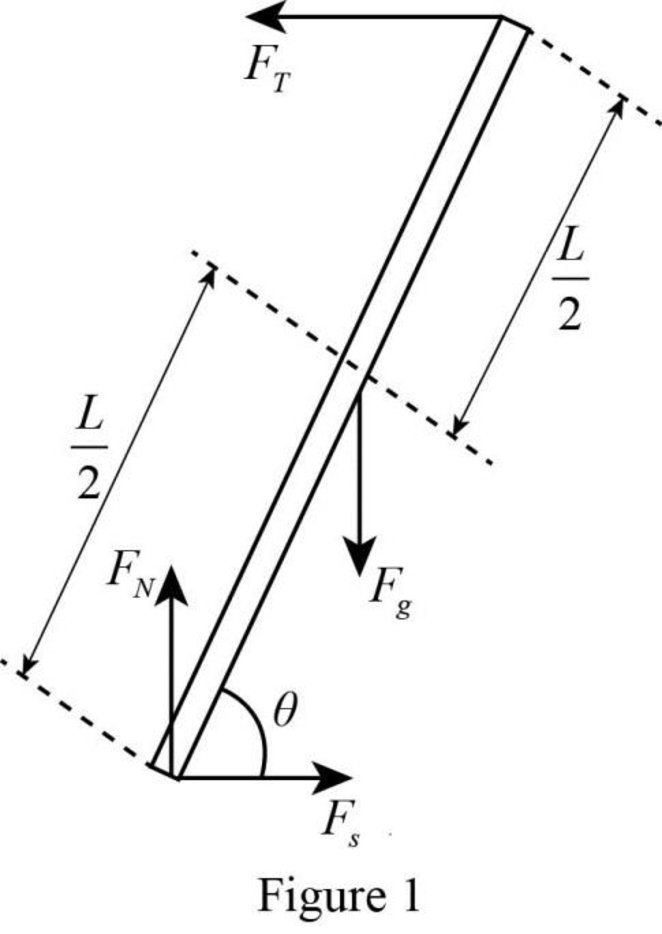
Explanation of Solution
A free-body diagram is a graphical tool used to illustrate the different forces acting on a particular object. It helps to solve complex physical problems. The free-body diagram of the ladder in the given situation is drawn in figure 1.
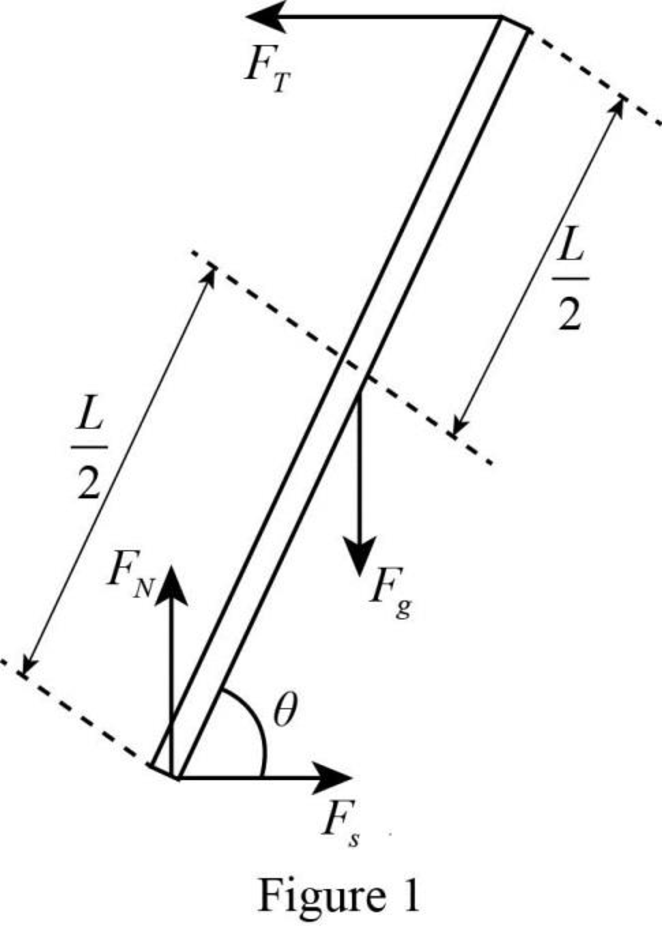
The forces acting on the ladder are the weight, the normal force, the tension and the force of static friction. In the figure weight is represented as
Conclusion:
Thus, the free-body diagram of the forces acting on the ladder is drawn in figure 1.
(b)
The tension in the rope in terms of
(b)
Answer to Problem 82PQ
The tension in the rope in terms of
Explanation of Solution
Take the lower end of the ladder as the pivot point. This will eliminate the torque due to normal force and the torque due to force of static friction.
Since the ladder is in rotational equilibrium, the net torque about the lower end of the ladder must be zero.
Write the condition for the rotational equilibrium.
Here,
Write the equation for
Here,
Put the above equation in equation (I).
Write the expression for
Write the expression for
Write the expression for
Here,
Write the expression for
Here,
Put the above four equations in equation (II) and rewrite it for
Conclusion:
Therefore, the tension in the rope in terms of
(c)
The expression for the tension in the rope in terms of
(c)
Answer to Problem 82PQ
The expression for the tension in the rope in terms of
Explanation of Solution
Since the ladder is in translational equilibrium, the net force in
Write the conditions for the translational equilibrium.
Here,
Here,
Write the equation for
Here,
Write the equation for
Here,
Put the above equation in equation (VI).
Put the above equation in equation (IV) and rewrite it for
Write the equation for
Here,
Write the equation for
Put the above equation in equation (VIII).
Put the above equation in equation (V) and rewrite it for
Put the above equation in equation (VII).
Conclusion:
Therefore, the expression for the tension in the rope in terms of
(d)
The coefficient of static friction in terms of the angle
(d)
Answer to Problem 82PQ
The coefficient of static friction in terms of the angle
Explanation of Solution
Equate equations (III) and (IX).
Conclusion:
Therefore, the coefficient of static friction in terms of the angle
(e)
The after effect of moving the ladder slightly so as to reduce the angle
(e)
Answer to Problem 82PQ
The ladder will slip if it is moved slightly to reduce the angle
Explanation of Solution
The expression for the angle
The expression for the tension force obtained in part (b),
Conclusion:
Thus, the ladder will slip if it is moved slightly to reduce the angle
Want to see more full solutions like this?
Chapter 14 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- please answer this asap!!!!arrow_forwardRT = 4.7E-30 18V IT = 2.3E-3A+ 12 38Ω ли 56Ω ли r5 27Ω ли r3 28Ω r4 > 75Ω r6 600 0.343V 75.8A Now figure out how much current in going through the r4 resistor. |4 = unit And then use that current to find the voltage drop across the r resistor. V4 = unitarrow_forward7 Find the volume inside the cone z² = x²+y², above the (x, y) plane, and between the spheres x²+y²+z² = 1 and x² + y²+z² = 4. Hint: use spherical polar coordinates.arrow_forward
- ганм Two long, straight wires are oriented perpendicular to the page, as shown in the figure(Figure 1). The current in one wire is I₁ = 3.0 A, pointing into the page, and the current in the other wire is 12 4.0 A, pointing out of the page. = Find the magnitude and direction of the net magnetic field at point P. Express your answer using two significant figures. VO ΜΕ ΑΣΦ ? Figure P 5.0 cm 5.0 cm ₁ = 3.0 A 12 = 4.0 A B: μΤ You have already submitted this answer. Enter a new answer. No credit lost. Try again. Submit Previous Answers Request Answer 1 of 1 Part B X Express your answer using two significant figures. ΜΕ ΑΣΦ 0 = 0 ? below the dashed line to the right P You have already submitted this answer. Enter a new answer. No credit lost. Try again.arrow_forwardAn infinitely long conducting cylindrical rod with a positive charge λ per unit length is surrounded by a conducting cylindrical shell (which is also infinitely long) with a charge per unit length of −2λ and radius r1, as shown in the figure. What is σinner, the surface charge density (charge per unit area) on the inner surface of the conducting shell? What is σouter, the surface charge density on the outside of the conducting shell? (Recall from the problem statement that the conducting shell has a total charge per unit length given by −2λ.)arrow_forwardA small conducting spherical shell with inner radius aa and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d (Figure 1). The inner shell has total charge +2q, and the outer shell has charge −2q. What's the total charge on the inner surface of the small shell? What's the total charge on the outer surface of the small shell? What's the total charge on the inner surface of the large shell? What's the total charge on the outer surface of the large shell?arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





