Chapter 14, Problem 6P

(a) Newton's method for approximating a root of an equation f(x) = 0 (see Section 4.8) can be adapted lo approximating a solution of a system of equations f(x, y) = 0 and g(x, y) = 0. The surfaces z = f(x, y) and z = g(x, y) intersect in a curve that intersects the xy-plane at the point (r, s), which is the solution of the system. If an initial approximation (x₁, y₁) is close to this point, then the tangent planes to the surfaces at (x₁, y₁) intersect in a straight line that intersects the xy-plane in a point (x₂, y₂), which should be closer to (r, s). (Compare with Figure 4.8.2.) Show that

$x_2=x_1-\frac{f{g}_y-f_{y}g}{f_x{g}_y-f_y{g}_x}$ and $y_2=y_1-\frac{f_{x}g-f{g}_x}{f_x{g}_y-f_y{g}_x}$

where f, g, and their partial derivatives are evaluated at (x₁, y₁). If we continue this procedure, we obtain successive approximations (x_n, y_n).

(b) It was Thomas Simpson (1710–1761) who formulated Newton's method as we know it today and who extended it to functions of two variables as in part (a). (See the biography of Simpson on page 520.) The example that he gave to illustrate the method was to solve the system of equations

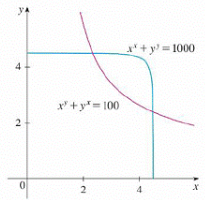
x^x + y^y= 1000 x^y + y^x= 100

In other words, he found the points of intersection of the curves in the figure. Use the method of part (a) to find the coordinates of the points of intersection correct to six decimal places.